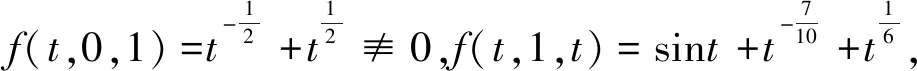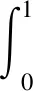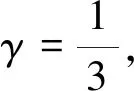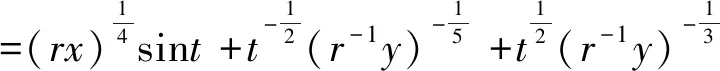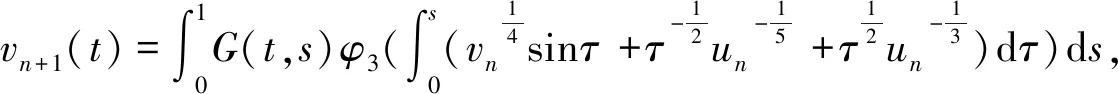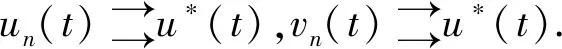带有p-Laplacian算子的奇异分数阶边值问题解的存在唯一性
2020-01-09王丽
王 丽
(曲阜师范大学数学科学学院,山东 曲阜 273165)
0 引 言
本文研究下述分数阶微分方程边值问题
(0.1)
解的存在唯一性.其中
是α阶Caputo型分数阶导数,φp(s)=|s|p-2s,p>1,f:(0,1)×[0,+)×(0,+)→[0,+),f(t,x,y)在y=0和t=0,1可以是奇异的.众所周知,φp是可逆的,它的逆算子是φq,其中常数q>1满足
近年来,分数阶微分方程在数学及其应用中都引起了广泛的关注,特别是应用于工程和科学研究的许多领域,如物理、化学、电力科学和生物学等,详情参见文献[1-7].带有p-Laplacian算子的分数阶微分方程的理论背景和应用,详情参见文献[8-10].此外,在该类分数阶微分方程中,其边值条件是积分形式的情况也引起了许多的关注,详情参见文献[11-14].
文献[10]研究了下列带有p-Laplacian算子的分数阶微分方程边值问题.
解的存在唯一性.其中
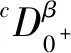
文献[14]研究了如下带有积分边值条件的非线性分数阶微分方程
正解的存在性.其中2<α<3,0<λ<2,f:[0,1]×[0,+)→[0,+)是连续函数.运用Guo-Krasnoselskii不动点定理证明了正解的存在性.
受以上文献的启发,研究问题(0.1)解的存在性和唯一性,其证明的主要方法是运用混合单调算子的不动点定理.不同于以上其他文章,本文中的非线性项f包含了可奇异的点.
1 预备知识
下面介绍分数阶微积分理论的相关定义和引理,其详情参见文献[1-3].
定义1.1函数u:[0,+)→R的α>0阶Riemann-Liouville型分数阶积分为
上式右端在R+内是诸点定义的.其中Γ(α)是欧拉Gamma函数,定义如下
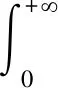
定义1.2函数u:[0,+)→R的α>0阶Caputo型分数阶导数为
其中n=[α]+1.
引理1.1[1]设α>0,则分数阶微分方程
cDαu(t)=0
有唯一解,其表达式为
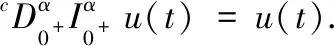
引理1.3[1]若α>0,n=[α]+1及u∈ACn[0,1],则

定义1.3[3]定义算子A:P×P→P,若A(x,y)关于x递增且关于y递减,即当ui,vi(i=1,2)∈P,u1≤u2,v1≥v2时,有
A(u1,v1)≤A(u2,v2),
则称A为混合单调算子.若A(x,x)=x.则称元素x为A的一个不动点.
引理1.4[3]设Ph⊂P,若A:Ph×Ph→Ph是混合单调算子,并且满足下列条件: 对于任意的u,v∈Ph和t∈(0,1),存在φ(t)∈(t,1),有
A(tu,t-1v)≥φ(t)A(u,v),
则算子方程A(x,x)=x有唯一正解x*∈Ph.同时,对于任意的初值x0,y0∈Ph,序列
xn=A(xn-1,yn-1),yn=A(yn-1,xn-1),n=1,2,…,
当n→时,有
2 主要结果
引理2.1设y∈C[0,1]∩L[0,1],2<α≤3,0<λ<2.则下列边值问题
(2.1)
有唯一解
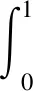
(2.2)
其中
(2.3)
证明对(2.1)的第一个方程在[0,t]上积分,得
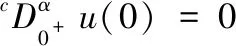
对上式两边作用φq,得
根据引理1.3,对上式两边求α阶积分,有
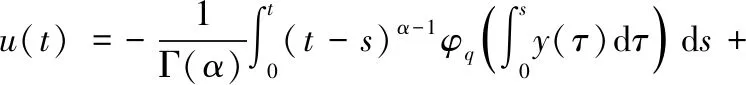
C0+C1t+C2t2.
(2.4)
再把u(0)=u″(0)=0带入(2.4),得C0=C2=0,因此
(2.5)
对(2.5)在[0,1]上积分,即
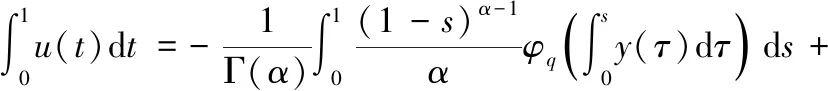
(2.6)
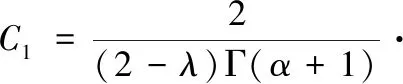
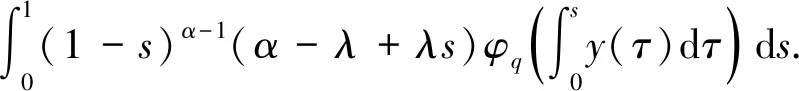
(2.7)
把(2.7)带入(2.5),可以得到边值问题(2.1)的唯一解是
(2.8)
其中G(t,s)是(2.3)所示的格林函数.证毕.
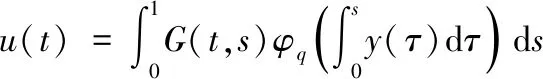
注1引理2.1中的边值问题与文献[14]中的边值问题方程不同,但是部分边值条件相同,使得所求的格林函数相同.所以本文中的格林函数与文献[14]中的格林函数具有相同的性质.
引理2.2[14]由(2.3)定义的格林函数G(t,s)满足下列性质:
(1)对于任意的s∈(0,1),λ∈(0,2),有G(1,s)>0;
(2)对于任意的t,s∈(0,1),λ∈(0,2),有G(t,s)>0;
(3)对于任意的t,s∈(0,1),λ∈(0,2),有J(s)t≤G(t,s)≤K(s)t,
其中
J(s)=G(1,s),
设Banach空间E=C[0,1],E中的范数是
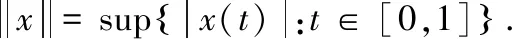
定义E中的锥P为
P={u∈E:u(t)≥0,对任意的t∈[0,1]},
并定义
(2.9)
其中h(t)=t,t∈(0,1).
在空间E中有锥P导出的如下偏序关系
x,y∈E,x≤y⟺x(t)≤y(t),对任意的t∈[0,1].
给出下列假设:
(H1)对任意的t∈(0,1),f(t,x,y)关于x递增且关于y递减;
(H2)对任意的x∈[0,+),y∈(0,+),t∈(0,1),存在γ∈(0,p-1),当0 f(t,rx,r-1y)≥rγf(t,x,y); (H3)对任意的t∈(0,1),有f(t,0,1)≢0并且 注2由(H2)可以推出,当r≥1时,有f(t,rx,r-1y)≤rγf(t,x,y);由(H1)知f(t,0,1) 定理2.1设(H1)—(H3)成立,则问题(0.1)有唯一正解u*∈Ph.对于任意的初值u0,v0∈Ph,序列 n=0,1,2,…, 当n→时, 证明考虑下列积分方程 (u∈Ph) 正解的存在性,其中G(t,s)是(2.3)所示的格林函数. 为此,定义算子A:Ph×Ph→P,其表达式为 首先,证明算子A:Ph×Ph→P是良定义的.对于任意的u∈Ph,v∈Ph,由引理2.2和条件(H1)—(H3),有 h(τ))dτ)ds (2.10) 那么,算子A:Ph×Ph→P是良定义的. 其次,证明算子A:Ph×Ph→Ph.对于任意的u∈Ph,v∈Ph,取 由(2.10)有 ≤Qu,vt=Qu,vh(t); 由条件(H2)和引理2.2,得 A(u,v)(t) 所以,有 从而得到算子A:Ph×Ph→Ph. 另一方面,验证算子A满足引理1.4的所有条件. 首先,证明A是混合单调算子.事实上,对于任意的ui,vi∈Ph,i=1,2,设u1≥u2,v1≤v2.由条件(H1)和φq的单调递增性,有 =A(u2,v2)(t). 因此,A是混合单调算子. 对于任意的u,v∈Ph,r∈(0,1),由条件(H2),可以得到 A(ru,r-1v)(t) =(rγ)q-1A(u,v)(t), 设φ(t)=(tγ)q-1,t∈(0,1),由0<γ(q-1)<1,可知对任意的t∈(0,1),都有φ(t)∈(t,1).所以, A(tu,t-1v)(t)≥φ(t)A(u,v)(t). 从而满足引理1.4的所有条件,那么,存在u*∈Ph,使得A(u*,u*)=u*.同时,对于任意的初值u0,v0∈Ph,序列 un+1=A(un,vn),vn+1=A(vn,un),n=0,1,2,…, 当n→时, 更确切地,当n→时,有 考虑下列例题 (3.1) 通过简单的计算得q=3. 可以验证,f(t,x,y)满足条件(H1). 那么,条件(H2)满足. f(t,rx,r-1y) 因此,它满足定理2.1的所有条件.那么,问题(3.1)有唯一的正解u*∈Ph,其中h(t)=t,t∈(0,1).并且,对于任意的初值u0,v0∈Ph,序列 其中G(t,s)是(2.3)定义的格林函数,当n→时,
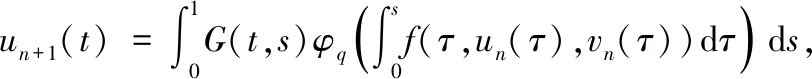
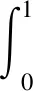
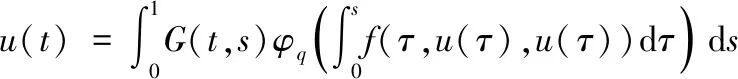
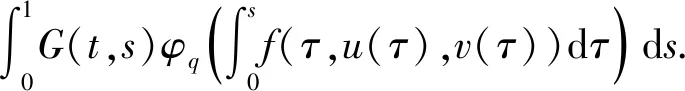
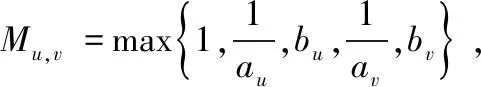
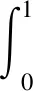
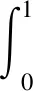
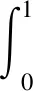
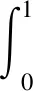
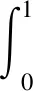
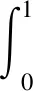
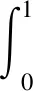




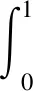
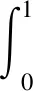
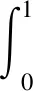
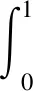
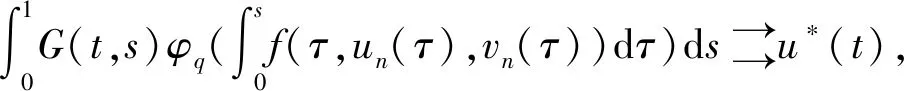
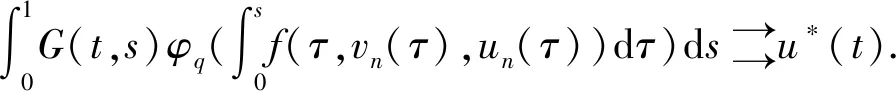
3 例 子