土体颗分曲线测试的密度计法取样量的影响分析

2020-01-09黄智超房营光

中国测试 2019年12期

黄智超，房营光,2

(1.华南理工大学土木与交通学院，广东广州 510641; 2.华南理工大学亚热带建筑科学国家重点实验室，广东广州 510641)

0 引言

土的粒径分布曲线是岩土工程建设的重要参考依据。颗粒粒径分析实验方法主要包括密度计法，激光静态散射法，电感应法等。激光静态散射法采用He-Ne激光产生的散射谱来测量粒径，电感应法的主要原理在于通过小孔电感应来测量粒度分布，激光静态散射法和电感应法优点在于精度高，测量时间短，但是实验设备成本高[1]。密度计法则是测定粒径小于0.075 mm土的粒径分布的实验室常用方法。本质上是利用斯托克斯定律来求解土粒在静水中的沉降速度，并换算成相应的试样颗粒粒径，特点是实现起来简单，成本低廉，应用广泛，但是也存在着精度低，误差大的缺点。

目前国家标准（GB/T50123-1999《土工试验方法标准》）关于密度计法土试样用量的取法规定为：取质量30 g的风干土经过0.075 mm孔径的筛进行筛选，将粒径小于0.075 mm土粒移入量筒中[2]。大量试验数据证明：同种土粒（粒径＜0.075 mm）的取样量差异会导致测定的颗分曲线出现偏差。为探究不同取样量对绘制颗分曲线绘制的影响以及修正密度计法的土颗粒沉降计算公式，提出的另一种土取样方案。该方案是直接筛取粒径小于0.075 mm的30 g土进行密度计实验，区别于国家标准中30 g试验土样先经过孔筛，然后进行密度计试验（此时粒径＜0.075 mm的土小于30 g，非定值）的取样方案。将以上两种方法命名为国标法和0.075 mm法以便于在文中区别。

国内外学者对该问题进行过深入探究，莫斯科大学在早1950年就讨论过不同土取样量对试验结果的影响，并认为20 ~50 g取样量为最佳试验取样区间[3]。Li Yuxia[4]在研究温度对颗分试验影响时从操作的角度提出了诸多降低颗分曲线误差的方法。陆天长[5]分析了沉降法中粒度分布的斯托克斯公式的适用条件。王自亮[6]应用“沉降原理”对测定粒径偏差问题进行了深入讨论。彭振阳等[7]分析了用土量对颗分结果的影响，认为用土量在30 ~40 g左右误差相对较少。但是目前相关研究的取样量，尤其是大于30 g的取样量的数据相对较少，且缺乏机制分析，对最优颗分取样量没有给出明确说明，也没有提出相应的改进方案。本文通过对砂土，黏土进行试验，研究了两种不同土颗粒的取样量对颗粒级配曲线绘制的影响，并用曲率系数Cc和不均匀系数Cu作对比，初步认为取样量导致了量筒中悬浮液的浓度差异，而浓度效应影响了土颗粒沉降过程，导致颗分曲线由于取样量不同而出现差异。考虑到土颗粒沉降的浓度效应，提出了新的可以对颗分试验进行修正的土颗粒沉降公式，初步认定GBT50123-1999《土工试验方法标准》关于土取样量规定会导致颗分曲线绘制的误差，并提出新的土取样量的方案（0.075 mm法），提高原有颗分试验的精度。。

1 不同取样量颗分实验及分析

1.1 不同取样量颗分试验及数据分析

该试验砂土样取自广州华南理工大学在建大楼的工地处，黏土样取自于该校图书馆附近。采用两种土是为了探究不同土性的取样量对颗分曲线绘制的影响。对土样中的大颗粒矿物（粒径≥2mm）进行剔除，并在自然状态下进行烘干。对两种类型的土分别采用国标法及0.075 mm法绘制颗分曲线，对于粒径大于0.075 mm的土粒采用振动筛分来进行粒径分析，小于0.075 mm的土颗粒均采用甲种密度计（TM-85）进行测量，二者其时间记录间隔均为：0.5，1，2，5，15，30，60，120，1 440 min[8]。

图1展示了密度计法颗分试验过程，为便于控制试验变量，国标法和0.075 mm法同时进行。左图为颗粒沉降过程，右图为密度计读数过程。

本实验以30 g取样量为标准，分别采用20 ，10 ，5 g粒径0.075 mm以下的土样和40 ，50 ，60 g粒径0.075 mm以下取样量为参照，注入纯水200 mL，并将其煮沸，然后通过研杵将其研碎，通过0.075 mm筛反复过筛，至杯底的沙粒洗净，得到小于0.075 mm的悬浊液[8]。利用该液体进行颗分试验，并绘制颗分曲线。

图1 颗分试验

比较图2、图3和图4、图5的不同土取样量颗分曲线，黏土和砂土颗分曲线均受到土取样量的影响，并以30 g为界，土颗粒含量越高对其颗粒级配曲线影响相对越小，取样量较低（20 g、10 g、5 g土）的颗分试验结果误差明显偏大，其中对于砂土来说，误差较大的级配区间在于0.01 mm至0.075 mm这个区段误差最高（0.075 mm以上土颗粒级配采用的是筛分法，误差很小），粒径0.01 mm以下的颗分曲线的误差变小，对于取样量30 g以上的结果认定在合理范围内。两种土颗分曲线误差主要区段在于0.04 ~ 0.075 mm之间。对于取样量小于30 g的土样误差约为10%~15%，对工程试验有影响。两者级配曲线整体趋势在于取样量高的颗分曲线高于取样量低的颗分曲线，取样量越大误差越小。30 g及以上取样量导致误差很小，工程试验中可忽略。

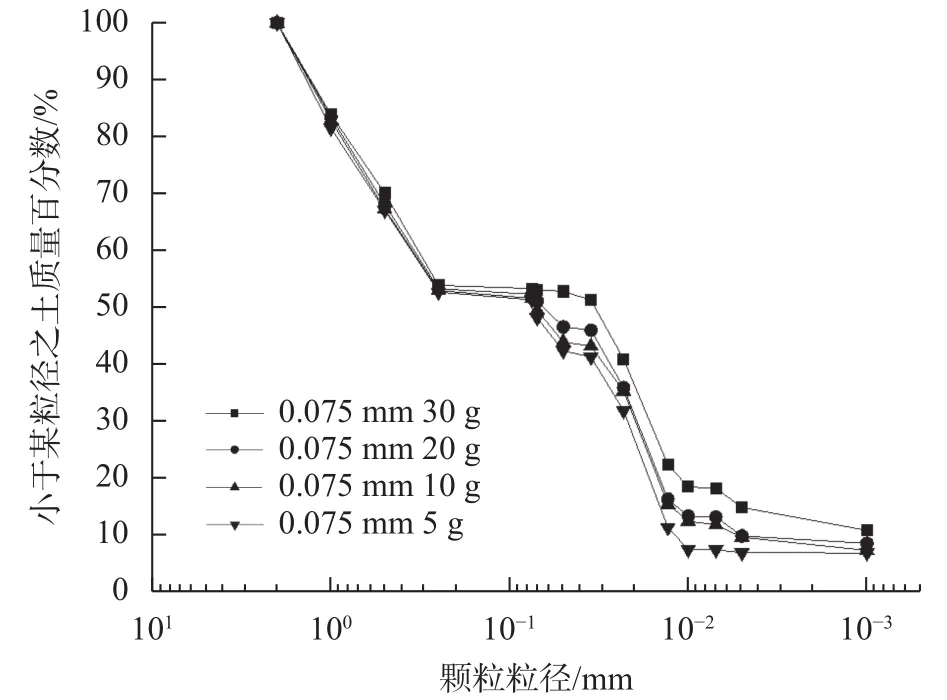
图2 砂土颗分曲线对比（30 g、20 g、10 g、5 g）

将以上的土样分为黏土1和砂土2土样，求出不同取样量下不均匀系数及曲率系数，绘制图6、图7。

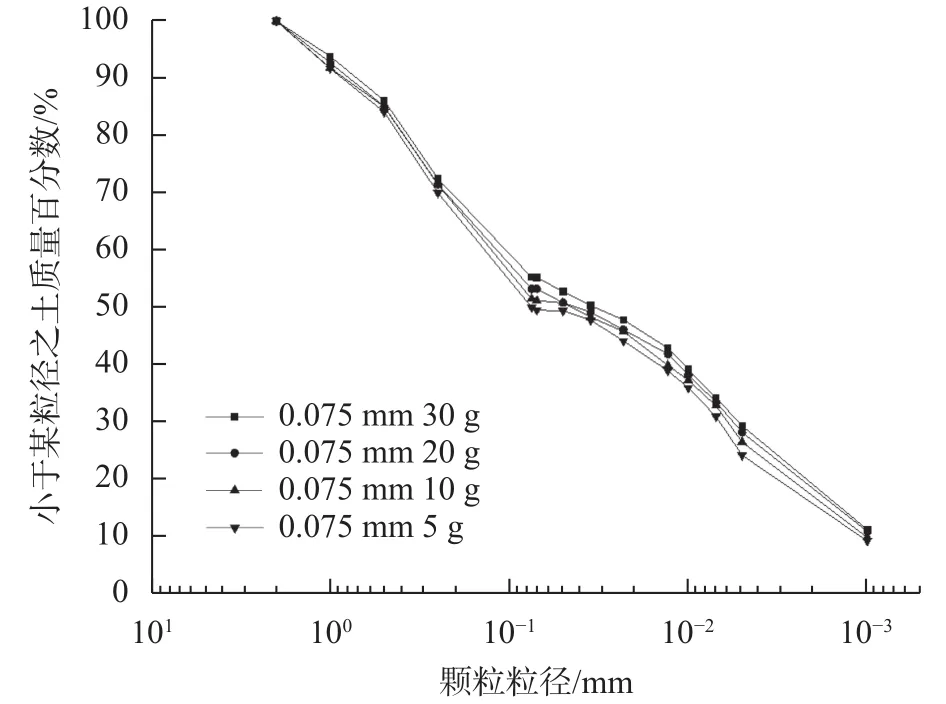
图3 黏土颗分曲线对比（30 g、20 g、10 g、5 g）

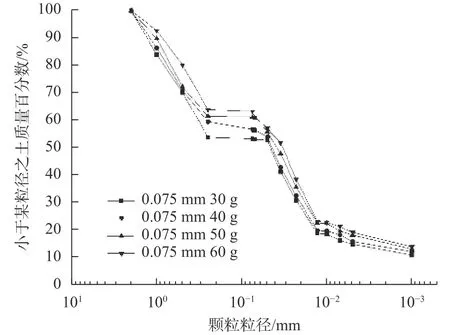
图4 砂土颗分曲线对比（30 g、40 g、50 g、60 g）

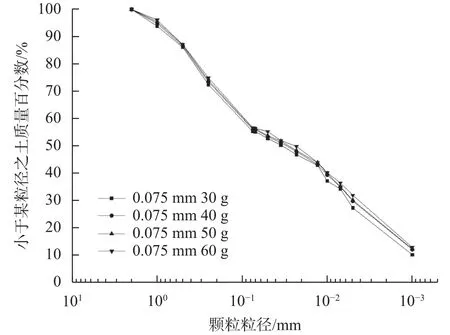
图5 黏土颗分曲线对比（30 g、40 g、50 g、60 g）

级配良好的土须满足以下条件：不均匀系数Cu≥5，曲率系数Cc=1～3。从图7可以发现取样量为5 g的砂土时其Cc∈[1,3]，但是采用10 g及以上取样量时，其曲率系数Cc＞3，这样就有可能由于土取样量的不同造成对土性质的判断错误，故有必要对原有试验方案进行改进。

从图6和图7可以发现取样量小于20 g的时出现明显的差异，且此时Cc、Cu明显偏小，且在20 g至60 g之间存在波动，但是对土样性质的判断影响较小。本文认为在30 ~60 g土质量对其试验造成的误差对于工程来说可以忽略不计。

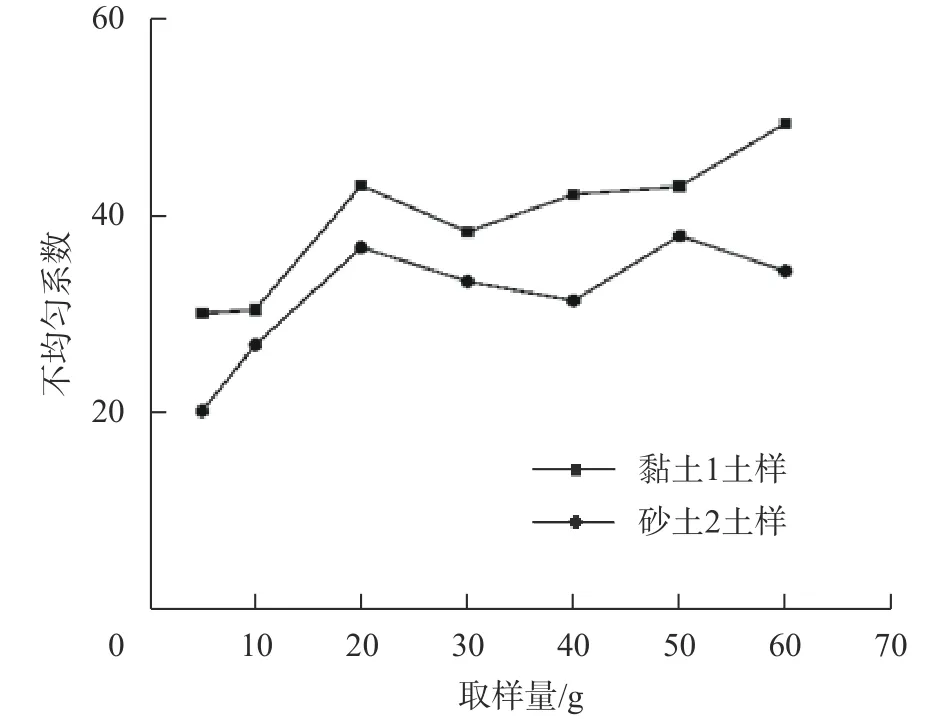
图6 土样的不均匀系数随土质量变化

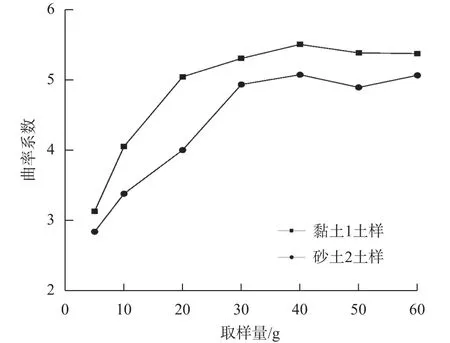
图7 土样的曲率系数随土质量变化

故原有的国标法的取样方案存在较大误差，可以采用本文给出的取样方法进行改进。

1.2 颗分试验理论改进

密度计法本质上是利用斯托克斯公式进行颗粒沉降的计算，再换算为粒径的分布。需满足以下假设[9]：1）球体运动极慢；2）液体介质的范围延伸至无穷远处，即介质中只有一个球形颗粒自由沉降；3）液体介质对于球的尺寸来说是连续的。但对于条件1难以满足，且土颗粒在沉降过程中产生压差阻力和摩擦阻力，现需要对斯托克斯公式进行修正[10]：

引入动量守恒方程[11]：

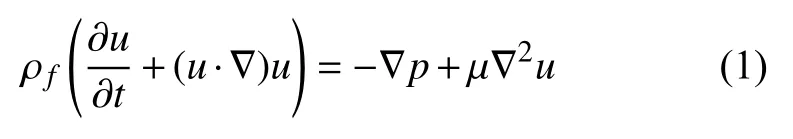
引入雷诺数进行修正[12-13]：

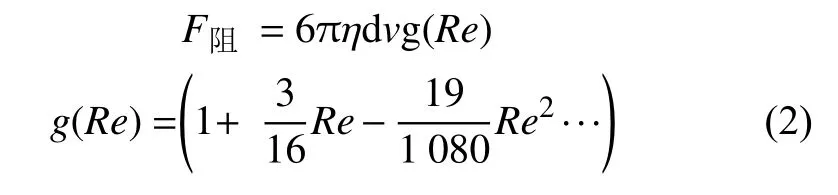
颗粒受到总的阻力与剪力等于流场应力对颗粒的总和：

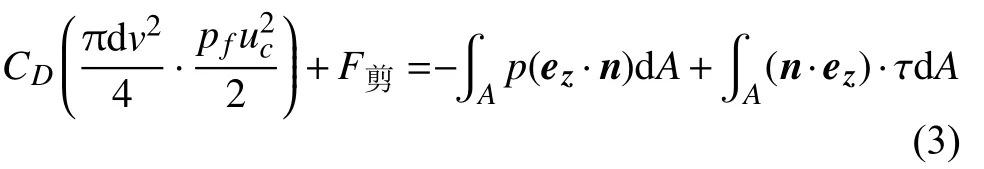
其中CD为颗粒阻力系数，p、τ为颗粒在流场中受到的阻力和剪切应力，通常颗粒粘性力可以忽略。

参考斯托克斯公式，将颗粒简化为椭圆型，建立颗粒沉降过程中受力方程式为：

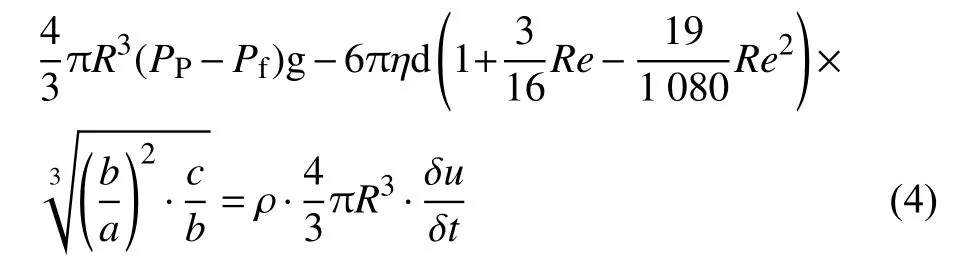
其中R为颗粒特征半径，PP、Pf为颗粒体积质量和体积浮质量。a，b，c分别为简化椭圆型颗粒的长轴，短轴和焦点。对于试验需要采用加速度仪进行测量，在精度要求不高的情况下忽略。

因为颗粒浓度变化引起悬浮液雷诺数的变化，故式（3）、式（4）初步认为是可行的，可以绘制更精确的颗分曲线。

2 土体颗分曲线的密度计两种方法测试试验

2.1 基于两种方法的测试结果

在0.075 mm法中，区别在于不同取样方法，对于密度计以及其他试验过程与国标法一样。取样方法是土样不是30 g风干土，而是利用0.075 mm孔径的筛进行筛选，筛出30 g小于0.075 mm土样，然后将其放入量筒，同时加水至1 000 mL，可以从以上实验操作中看出两者最大的不同在于进入量筒粒径小于0.075 mm的土样，国标法是不可控的，相反0.075 mm法是定值。其他操作按照国家标准进行试验，其试验方法同1.1节试验一样。颗分曲线绘制结果见图8、图9。

2.2 两种规范方法测试的问题分析

为比较以上两种方法的优劣，土样1为砂土样，土样2为黏土样，并将国标法的试验数据以斯托克斯定理和1.2节公式分别进行计算绘制颗分曲线，并新命名为国标法修正。0.075 mm法仍采用斯托克斯定理进行计算。进行上述试验，得到以下颗分曲线结果。

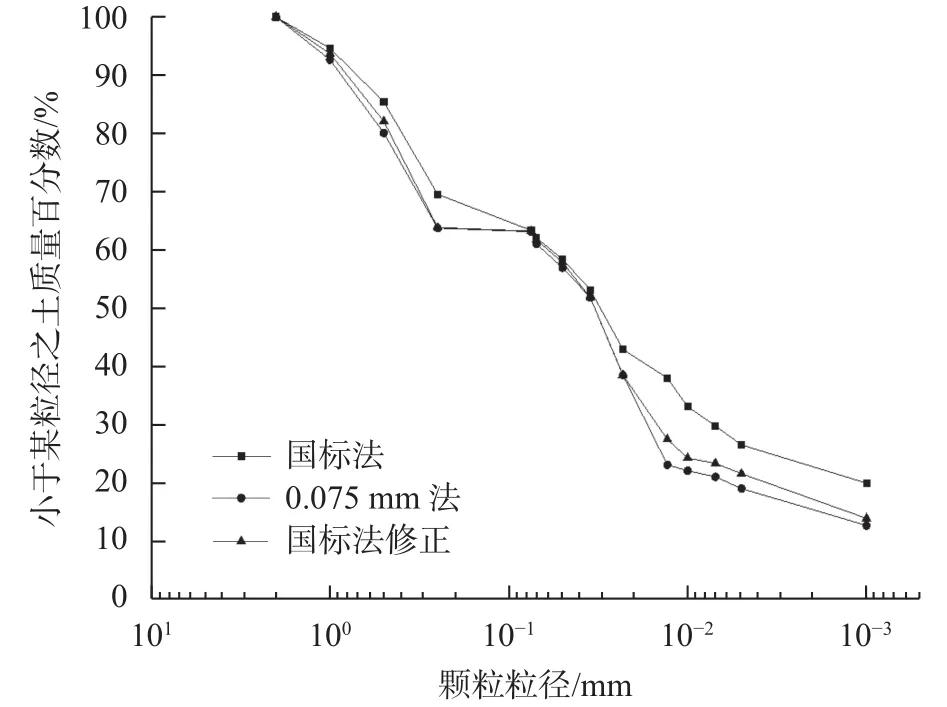
图8 砂土颗分试验曲线（土样1）

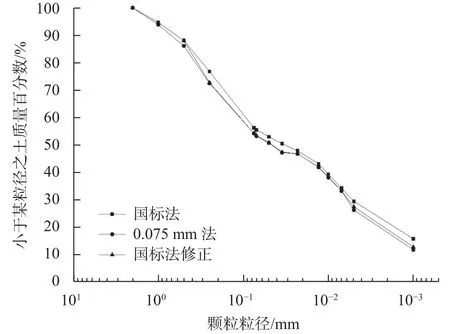
图9 黏土颗分试验曲线（土样2）

比较图8和图9可以发现：由于粒径＞0.075 mm的颗分试验均是采用孔筛进行筛分得到，与二者颗分曲线上半段几乎重合的规律符合。当试验对象为砂土时，密度计在粒径0.01 mm以上曲线差别不大，但是在粒径极小（粒径＜0.01 mm）时，国标法曲线偏上，说明这个粒径范围内密度计测出来的值偏低。同样在黏土颗分试验中，发现仍是国标法曲线比0.075 mm法曲线偏上。

从图像上得到砂土颗分曲线（0.075 mm法）初期只有极微幅度的下降，但粒径在0.05 mm内时，颗分试验下降幅度变大，且在0.01 mm之后与国标法修正绘制曲线下降幅度基本一致，呈平行的关系。对比发现，改进公式对黏土的影响相对较小，二者曲线有接近重合的趋势。

国标法采用1.2节公式修正过后的砂土颗分曲线与本文0.075 mm法作出的颗分曲线更接近，相对误差更小，也证明0.075 mm法的颗分曲线的精度明显要优于国标法，也进一步说明1.2节公式推导有一定的合理性。

采用国标法取样量作出的颗分曲线与本文采用的0.075 mm法取样量做出的曲线有一定差异，且对黏土曲线影响较小，但是对砂土影响大。

因此原国标法做出的曲线可以采用1.2节所提出的公式进行修正。

3 密度计法取样量误差原因分析

关于土体颗分沉降法的现行国家标准中规定，取质量为30 g的风干土，由0.075 mm孔径的筛进行筛分，将其中粒径小于0.075 mm的土粒进行沉降分析法试验，测得颗分曲线。从30 g不同土干中筛分得到的粒径小于0.075 mm颗粒质量是不同的，由此制备的沉降试验的悬浮液浓度不同，由于土颗粒沉降群体行为的浓度效应而产生误差[13]。砂土砂粒含量高，颗粒直径大，容易聚集形成团粒，下降速度变快，浓度效应显著，土取样量对颗分曲线影响更大。而黏土粒径小，比表面积大，颗粒表面能高，表面极性大，相互排斥，不容易形成团粒，浓度效应不明显[14]。

而0.075 mm以下的砂土取样量直接定为30 g（可以从300 g土试样筛选然后定量称取），可以减少原有国标法中不同土取样量导致的颗粒浓度的影响。黏土由于影响较小，可以不采用改进取样方法。

如果仍采用国标法取样，对于不同取样量的颗分曲线可以采用式（3）、式（4）来计算其颗粒沉降速度，再换算为颗粒粒径分布的计算，也可有效减少浓度效应带来的颗分曲线绘制的误差。