双板装置的测角偏差及修正方法研究
2020-01-09薛光明钱明军王志文
薛光明,石 昊,钱明军,王志文,王 可
(中国人民解放军63969部队,江苏 南京 210028)
0 引 言
车辆通过角是反映车辆通过性能的重要参数,也是汽车试验的重要项目[1]。当前测量车辆通过角的方法主要是通过测量车体突出点距离、高度,然后基于轮胎的静力半径或自由半径进行计算[2-4]。该方法计算精度较高,但是计算过程较为复杂,后续处理较难,同时突出点的位置通过肉眼进行判断,十分依赖试验员经验,难以进行精度论证。
测距法是一种汽车试验领域最常用的间接测量法,部分学者还基于机械设计[5-6]、红外光幕[7-8]、激光测量[9-10]或图像识别[11-12]等技术手段进行测量,可直接测量出车辆通过角,或先辨识车辆轮廓或尺寸参数,再计算出车辆通过角度。这些手段测量结果准确有效,但实施需要复杂仪器和专业知识,对于普通技术人员存在执行难度,同时在误差分析上难度较高,不利于后续标准的制定。除上述手段外,基于其原理的通用测角方法[13]也可用于车辆通过角的测量。
对比上述方法,采用双板进行测量是最直观的测量法,能够模拟车辆真实的通过情况,测量角度准确且易于实施。然而采用双板测量车辆接近角或离去角存在的最大难点就是板的厚度问题,当测量板具有一定厚度后,在待测角较小时难以保证与轮胎相切,此时实测角并非精确角,测量存在偏差。本文针对该问题,对测量有效和失效的情况进行分析,并计算失效测量偏差,提出对应的修正方案,为车辆角度的测量提供一种新的技术手段。
1 测量原理
双板测量车辆通过角的原理如图1所示。其中,A为测量接触面与车体突出位置的接触点,B为测量板端点,G为两板的铰接点,Q为车轮中心点。以车轮接地的最低点为坐标轴轴心O,水平方向为x轴,竖直方向为y轴,可建立图中所示的xOy坐标系。
如图1(a)所示,当测量板上表面与车轮相切时,两板之间的夹角等于待测的通过角,测量结果有效;如图1(b)所示,当测量板上表面无法与轮胎相切,而与车轮交于端点B时,两板之间的夹角为割线AB与基准板之间的夹角,而不是由A点引出的切线夹角,因而不等于待测的通过角,这种情况下测量无效。下面对测量有效和失效的情况进行分析,以确定可行的测量范围并对失效情况进行修正。

图1 双板测量原理
2 有效测量范围
2.1 临界情况
首先分析测量的临界情况,即测量板上平面与轮胎相切时,且切点恰为B。此时,QBG共线且与AB垂直,则∠OQB恰为所测临界角α0,此时有
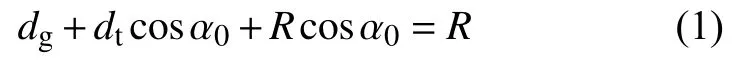
式中:dt、dg——测量板厚度、基准板厚度;
R——车轮半径。
求解可得测量临界角度为

易知,当测得角α不小于式(2)给出的临界角时,测量板上表面能够与轮胎圆相切(仅在临界条件下切点为B),实测角即为车辆的实际通过角,测量结果是有效的。
2.2 有效测量时测量板厚度
由式(2)可知,当待测实际角α≥α0= arccos[(R-dg)/(R+dt)]时,采用双板测得角为精确角,整理该不等式,可得适用的双板结构形式需满足

因此,若要对车轮半径为R、通过角为α的车辆进行有效测量,所采用的测量板和基准板厚度应满足式(3)。以dg为横轴,dt为纵轴,式(3)对应了图2所示的三角形阴影区域。有效测量时基准板和测量板的厚度参数应处于图2中所示三角形区域(含边界)。当板的厚度参数处于图2中所示三角形之外时,实测角要小于精确角,直接测量结果失效。

图2 有效测量时装置参数范围
2.3 装置的有效测量范围
当测量装置尺寸已知后,根据式(2)同时可得测量有效时的最小角度值,其结果如图3中曲面所示。当待测车辆的通过角数值处于曲面上方时,装置的测量结果是有效的,而当待测角处于曲面下方时,测量结果是无效的。

图3 有效测量的最小角度
由图3可知,dt/R、dg/R越大,双板进行有效测量时的最小角越大,即测量范围越小。若要降低有效测量角的最小值,即增大测量范围,应尽可能减小dg和dt与轮胎半径R的比值。
对于测量装置而言,测量板和基准板越薄,有效测角最小值越小,装置测量范围越大。对于车辆而言,轮胎半径越小,所需测量板和基准板的厚度越薄。也就是说,若测量装置适用于轮胎半径较小的情况,必适用于轮胎半径较大的情形。
2.4 等双板情形
一般情况下,为加工方便,测量板和加工板一般厚度相等,即dg=dt。此时,式(3)转化为

为具有通用性,测量装置应能适用于最小尺寸的轮胎,考虑到绝大多数车辆轮胎半径不小于29 cm,应代入该最小尺寸进行计算,可得到板厚度与最小可测角的关系如图4所示。
由计算结果可知,对于大部分越野车辆,其通过角不小于20°,所用测量板厚度最好不超过1 cm;对于家用车,其通过角约为10.5°,所需测量板厚度应不超过0.25 cm。如此薄的板对选材和制造加工提出了一定要求,同时要避免在使用时必然产生较大的弯曲变形,导致测量结果不准确。

图4 不同板厚度下的最小可测角
3 测量失效情况
当测量板上平面与轮胎圆相交而非相切时,测得角为割线AB与基准板平面之间的夹角,考虑到车辆实际的通过角为切线与基准板平面之间的夹角,此时实测角较精确角要偏小。
3.1 失效时实测角αB
下面对该种情况下的实测角进行计算。由图1(b),B点和G点的距离等于板厚度dt,同时有直线BQ⊥AB,若记实测角为αB,可得测量装置的固有方程为
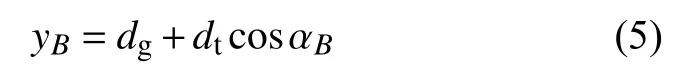
其中yB为B点的纵坐标值。
B点在直线AB上,则有

式中:xB——B点的横坐标值;
l、h——分别为测量点长度和高度。
同时,B点在圆Q上,可得

联立式(5)、(6)和(7),可求得实测角αB的隐式方程为
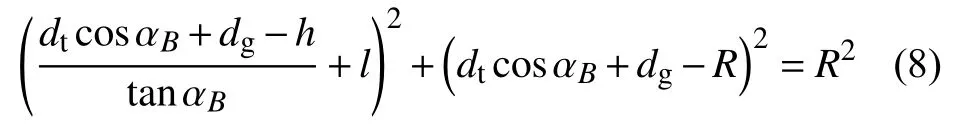
该方程不具有解析解,可采用一维搜索方法进行数值求解。
3.2 精确角αe
下面分析车辆通过角和离去角的精确值αe。过A点引圆Q的切线,该切线的斜率即为车辆实际角的正切值。若记切点为E,E点坐标为(xE,yE),切线AE的斜率为tanαe,则E点满足在切线AE上、在圆Q上、QE与AE垂直这三个条件,对应方程为

求解该方程,可得精确角αe的余弦值满足

3.3 测量失效时的修正
3.3.1 测量偏差
综合3.1节和3.2节中的分析结果可知,实测角α与车辆通过角的精确值αe之间的关系为

式中,α0、αB、αe分别由式(2)、式(8)、式(10)给出。
同时测量是否有效可直接从观察判定,若测量板上表面与轮胎相切时,意味着实测角不小于临界角,则测量角度等于精确通过角;若观察到测量板上表面与轮胎相交,则实测角小于临界角,同时也小于实际通过角。
图5给出了无法实施有效测量时实测角与精确角之间的差异。由曲线可知,当待测角不大于式(2)给出的临界角时存在偏差,且该偏差随待测角的增大而减小;当待测角超过临界角时,测量偏差变为0。
定义测量偏差Δα为精确角与实测角的差值,下面对该测量偏差进行补正,希望通过对测量角进行适当处理以得到精确角。
由式(10)给出的精确角和式(8)给出的实测角表达式可知,实测角或精确角与轮胎半径R、板厚度dt、测量点长度l、测量点高度h有关。将式(8)中方程两边同时除以R2,式(10)右侧分子分母同除以R可知,实测角或精确角与各尺寸参数与轮胎半径R的比值有关,即与dt/R、l/R、h/R有关。考虑到实测角为已知量,相当于这3个量有一个为确定量,只需分析dt/R和l/R两个量的影响即可分析得到测量偏差。
3.3.2 板厚度的影响
下面分析这两个参数对测量偏差的影响。令l=2.5R,即测量点长度为车轮半径的2.5倍,图6(a)给出了不同dt/R时的测量偏差曲线。由计算结果可知,dt/R越小,即车轮半径固定时,测量板越薄,偏差曲线整体下移,失效时的测量偏差也越小。

图5 精确角和实测角

图6 dt/R对测量偏差的影响
调整l/R的数值时,曲线形式不变,但在纵轴的截距即偏差最大值具有较大影响。计算不同l/R下的最大偏差值如图6(b)所示,由计算结果可知,偏差最大值与dt/R之间的关系为正比例关系,该比例系数与测量点长度l有关,l/R越大,测量偏差的最大值减小,这意味着测量偏差也在逐渐减小。
3.3.3 测量点长度的影响
令dt=0.1R,计算得到l/R对测量偏差的影响曲线如图7(a)所示,同时不同dt/R下的偏差最大值如图7(b)所示。由结果可知,l/R越大,即测量点距离越远,偏差曲线整体下移,测量偏差较小;测量偏差与R/l也大致成正比例关系,且当R/l增大,即测量点较近时,测量最大偏差逐渐增大,亦即测量偏差变大。

图7 l/R对测量偏差的影响
3.3.4 偏差修正
针对3.3.3节分析的偏差情况,可以基于实测角编制修正图对测量结果进行修正,以得到较为精确的计算结果。考虑到轮胎尺寸为标准尺寸,测量板在应用推广后尺寸也会标准化,而车辆的测量点长度等参数不会固定。因此,偏差修正图最好以测量点位置的影响曲线为基础,根据常用的轮胎尺寸和测量板尺寸多绘制几个修正图即可。
图8给出了dt=0.1R时的修正曲线图,根据实测角α、l/R的估计值可查得测量偏差,然后将实测角加上查得的偏差值即得最终的角度测量值,未落在曲线上的偏差值可由曲线上点值进行估计。举例说明该图的用法,如待测车辆的自由半径为30 cm,采用dt=3 cm的测量板进行测量,可选择所示的修正图进行修正;若测得角为10°,同时估算测量板位置约为轮胎半径的2.0倍,查图可知,修正角约为3.3°,因而确定实测角为10°+3.3°=13.3°。

图8 测量偏差修正图
4 结束语
双板式测量方法在测量车辆通过角时存在最小临界角,待测角不小于临界角时,测量结果直接有效,为降低临界角,应尽可能地减小测量板的厚度。待测角小于临界角时,测量结果无效,且板厚度越薄,测量点长度越大,测量失效时的偏差越小,同时,测量偏差可通过建立修正表予以补正。
