地下爆炸炸点定位方法及布局精度分析
2020-01-09闫佳晖张晓明
闫佳晖,张晓明
(中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引 言
地下炸点定位中,由于炸点在地下,可用于定位的信息比较少,主要利用爆炸产生的冲击波和振动波判别炸点位置。冲击波、振动波使介质质点产生位移、速度和加速度[1-5]。所以可以通过以上信息进行炸点定位测量。其中加速度的测量现如今可以通过MEMS技术实现小型化和高精度的测量。基于这项技术的三轴振动传感器和数据采集系统即可采集爆炸时产生的振动信号。由于传感节点布局位置不同,振动信号传入不同传感节点会产生时间差,从而可反算出炸点到达传感节点的距离差信息,以此对爆炸炸点进行定位。另外,由于爆炸振动波的矢量传播特性,可以通过三轴振动传感器得到炸点相对于传感节点的角度信息。由以上两种信息可通过TDOA及AOA等[6-8]定位算法计算爆炸场炸点位置。在定位过程中,对传感节点布局和定位算法精度的研究是很必要的。文献[9]提出4个传感节点布局指标,利用成像技术进行定位,实现使用最少传感节点重建最高还原精度爆炸场,但是其节点布局影响因子仅针对成像技术定位方法的精度分析。文献[10]利用时空域数据融合技术提高炸点定位,但是该方法仅适用于低频光电经纬仪的定位系统中,并且缺乏定位算法精度的分析。文献[11]提出利用声波和地震波传播到达节点的时间差进行定位,并对定位影响因素做出分析,文献[12]在原有四元十字阵的基础上改进为五元十字阵,描述的测距和测角定位算法在此构型中的定位精度,但是缺少对传感节点布局对定位精度影响的评估方法。上述文献精度分析都不够直观,大多采用实验方法提出系统精度,不能从设计的角度提出指导意见,应用场景局限性较为明显。
针对现有的地下炸点定位精度分析方面的不足,提出一种定位精度计算方法,并通过定位精度的准确度、稳定度指标对不同算法和布局完成评估[13],为后续实验提供方案评估和理论支持。
1 定位原理及误差分析原理
1.1 地下爆炸波定位原理
为了定位地下爆炸炸点位置,分析其传播特性。理论分析时,定位区域范围内土壤可以视为均匀介质,振动波传播距离与时间之间存在线性关系,即

其中s为振动波传播距离;v表示振动波在均匀介质中的传播速度,通过实验可以测得;t表示振动波在介质中传播时间。通过式(1)中关系,传感节点得到振动波的到达时间,从而得到节点与炸点的距离。在TDOA定位算法中,通过传感元件获得待定位点信号到各个传感节点时间戳,构建N个伪距方程组成的非线性方程组。待定位点到传感节点的伪距方程为

其中si为待定位点到第i个传感节点的伪距,(x,y,z)为待定位的坐标点;(xi,yi,zi)为已知的第i个传感节点坐标,v为通过预实验测出的振动波在土壤中的传播速度,为待定位点信号传播到传感节点所经历时间中的时钟偏移,导致si存在测量误差。图1中s1即为炸点与节点1的距离。
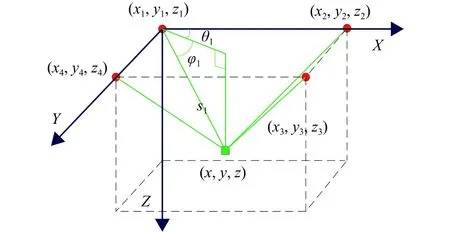
图1 定位区域示意图
另外爆炸振动波传播具有矢量性,可以通过测量振动波传入传感节点的入射角度对炸点进行定位。图1中θ1和φ1分别为节点1测得的炸点水平角和竖直角。根据几何关系,水平角及竖直角与待定位炸点坐标和传感节点坐标之间关系可表达为

基于以上传播特性,通过测量振动波到传感节点的到达时间和到达角度,即可对炸点进行定位。设计三轴振动传感器集成于传感节点中,配备数据采集单元,将传感节点安装在统一的时空基准下,完成地下爆炸炸点的定位。使用系统完成对地下爆炸的炸点定位,存在对节点布局及定位算法选择的问题。建立一套精度评价体系,对实际应用中炸点定位系统定位精度做出评估。
1.2 定位算法及误差分析原理
1.2.1 基于TDOA定位算法的误差分析
对于式(2)取炸点附近一点坐标(x0,y0,z0),一阶泰勒展开得:

对上式整理可得:

当定位节点数大于4时(即n>4),求解式(6)的非线性方程组,利用最小二乘法可得:
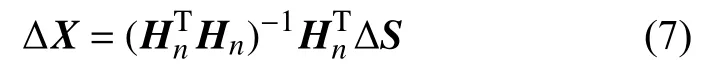

伪距误差被认为是随机变量,式(8)将ΔX表示成与ΔS呈函数关系的随机变量。假定误差矢量ΔS具有一些分量,这些分量是期望为零且为联合高斯分布的。在认为几何布局固定的情况下,由此得出ΔX也服从高斯分布,且期望为零。由于ΔX与ΔS中各分量相互独立,根据数学期望和方差性质可得:
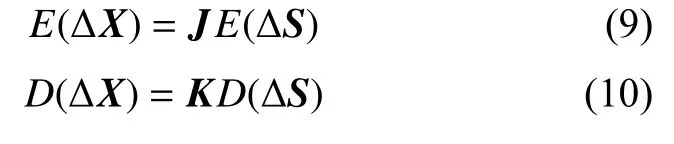
其中K矩阵元素大小为J矩阵中对应位置元素值的平方。
1.2.2 基于AOA定位算法的误差分析
对式(3)、式(4)进行反三角函数变换,然后一阶泰勒展开得:

其中:

对上式整理可得:

对上式进行最小二乘变换。
由于ΔX与ΔS中各分量也相互独立,同理可得误差精度计算方法。

1.2.3 TDOA和AOA融合定位算法误差分析
沿用1.2.1和1.2.2所述的原理模型,如上文所述的基于TDOA和AOA定位算法精度计算,通过结合两者测量数据(到达时间差和水平角及竖直角)可以得到:

其中每个传感节点提供3个测量数据,分别为炸点冲击波到达传感节点时钟值,待定位爆炸点相对于传感节点的水平角及竖直角。各个传感节点测到的3个分量相互独立,根据式(9)、式(10),同理可得X、Y、Z轴定位误差分量和3个测量分量之间的期望和方差关系。
2 仿真结果及分析
2.1 仿真环境及参数
爆炸场炸点定位要求定位长200 m宽200 m深10 m的长方体区域。如图1所示,虚线围成的区域为炸点待定位区域,其中4个红色圆点围成平面为地平面,绿色正方形小块表示区域内待定位点。以(x1,y1,z1)为三维坐标系原点,分别以X、Y、Z轴正方向构建三维地理坐标系。沿Z轴正方向分5层对区域进行仿真。
现有的炸点定位系统经事先标定时钟准确度为18 μs,振动波传播速度为5 500 m/s,计算可知测距准确度约为10 cm,水平角θ误差为1°,竖直角φ误差为0.5°。
2.2 仿真结果
2.2.1 算法对比
为了研究定位算法不同对区域定位精度造成的影响,分别采用TDOA,AOA定位算法及TDOA和AOA融合算法对定位区域进行仿真。本节将讨论不同算法对于表1中传感节点布局3定位精度分布趋势。使用2.1所述环境及参数,TDOA定位算法精度仿真结果如图2和图3所示,AOA定位算法精度仿真结果如图4和图5所示。融合定位算法精度仿真结果如图6和图7所示。

图2 TDOA算法的水平定位精度分布

图3 TDOA算法的垂直定位精度分布

图4 AOA算法的水平定位精度分布

图5 AOA算法的垂直定位精度分布
对于TDOA定位算法,水平精度最高的区域分布在靠近地表的4个节点表面内,而随着深度的增加,垂直定位精度不再变化,并且精度都较高;在其他区域随着深度增加,各层的定位误差分布基本相同,以中心区域精度最高,呈环形向外减小。

图6 布局3融合算法的水平定位精度分布

图7 布局3融合算法的垂直定位精度分布
对于AOA定位算法,精度最高的区域分布在靠近地表的4个节点表面内;在其他区域随着深度增加,各层的水平定位精度在增大,以中心区域精度最高,呈环形向外减小;而垂直定位精度中心区域随着深度增加,精度减小。
对于融合定位算法,精度最高的区域分布在靠近地表的4个节点表面内;在其他区域随着深度增加,各层的水平定位误差在增大,而垂直定位误差先减小后增大再减小,以中心区域精度最高,呈环形向外减小。
3种算法在各深度层的定位精度平均值和标准差分布趋势如图8、图9所示。对比两张图,可以看出TDOA算法的优势在于水平方向的定位精度较高。但垂直方向精度比较差;AOA算法优势在于垂直定位精度高,在各层间精度分布比较稳定,无论是从某一深度还是整体来看,AOA的定位精度波动不大,稳定度较高,但是水平定位精度较低。而融合定位算法优势体现在比另外两种算法都高的水平定位精度以及在可接受范围的垂直定位精度。

图8 算法分层定位精度平均值分布
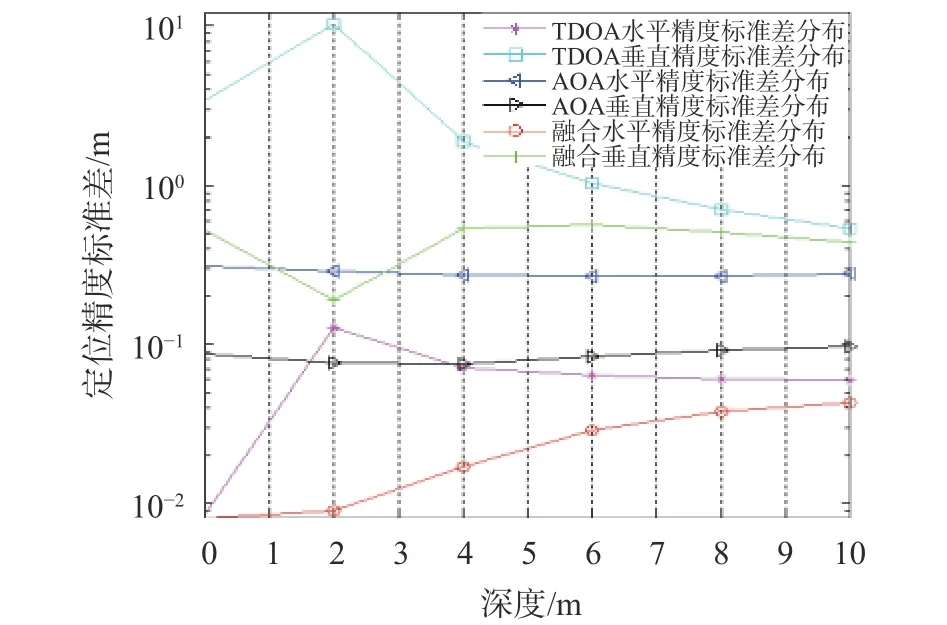
图9 算法分层定位精度标准差分布
因此,在更加关注垂直定位精度的场合中单独使用AOA定位算法会更好,而关注水平定位精度的场合中使用融合算法进行定位解算会得到更理想的定位坐标。
2.2.2 基站数目和布局对比
为了研究传感节点布局不同对区域精度分布规律造成的影响,使用4个传感节点以两种布局进行布置,另外为了探究基站数目对分布规律的影响,提出了布局3。布局节点坐标如表1所示。

表1 传感节点布局坐标
布局对比主要分析布局对定位精度分布产生的影响,仿真分析均在融合定位算法下进行。对于布局3的定位精度分布如图6、图7所示,布局1和布局2的定位精度分布如图10、图11和图12、图13所示。
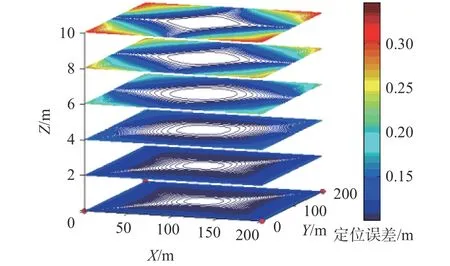
图10 布局1的水平定位精度分布
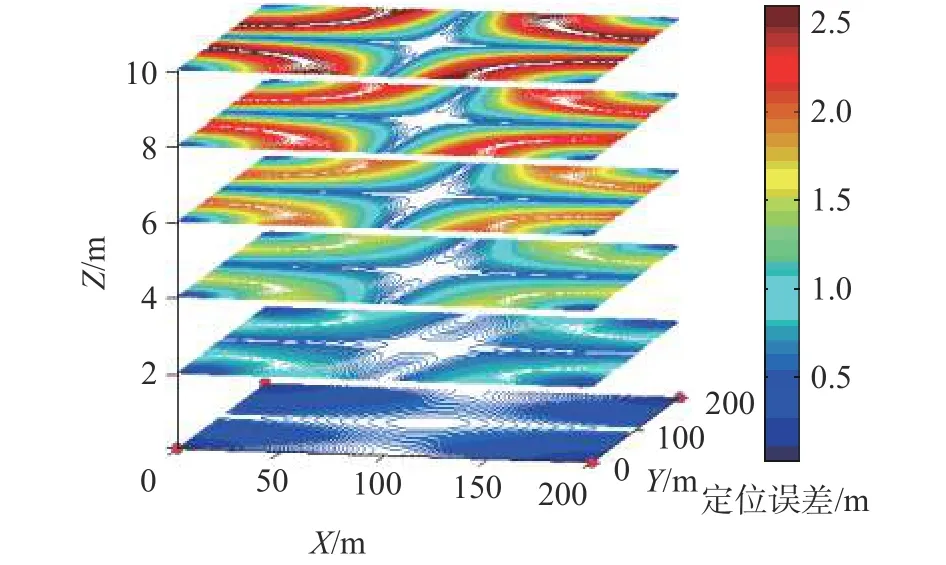
图11 布局1的垂直定位精度分布
对比不同布局定位精度分布图可以看出在同一水平面内,靠近于节点和节点所围几何图形的内部定位精度较高,随着深度增加,定位精度从定位区域边缘开始逐渐变差。就定位精度的最大小值来看,在传感节点数目都为4时,布局1对当前区域的定位效果较好。在布局3中可以看出,节点所在坐标直接影响到相同水平坐标不同深度的定位精度,距离节点距离越小,水平精度越好,垂直精度较差。
不同布局下分层定位精度平均值和标准差对比如图14、图15所示。可以看出布局1的垂直定位精度随着深度增加逐渐变差,定位波动性也在增大。在深度8.5 m以上,布局1优于布局2;8.5~10 m则布局2优于布局1。比较布局1和布局3可以看出,增加传感节点后,垂直定位精度波动性变小,稳定性提高。
综上所述,AOA定位算法的优越性表现在其垂直定位精度上,而融合定位算法的优越性表现在其总体的定位精度上。对于布局选择,分别从精度值分布、分布平均值、标准差3个因素进行评价。精度值分布直观反映局部定位相对总体区域的好坏;分布平均值反映当前算法和布局下定位的准确度;标准差反映当前定位条件下在目标点坐标不同时的精度波动性。从总体定位精度来看,布局1表现最好,从定位精度波动性来看,炸点深度在8 m以下布局1较好。8 ~10 m布局2较好。增加节点数目可以增加系统对不同深度的定位精度稳定性。
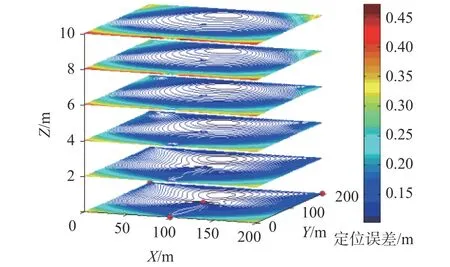
图12 布局2的水平定位精度分布

图13 布局2的垂直定位精度分布

图14 不同布局分层定位精度平均值分布
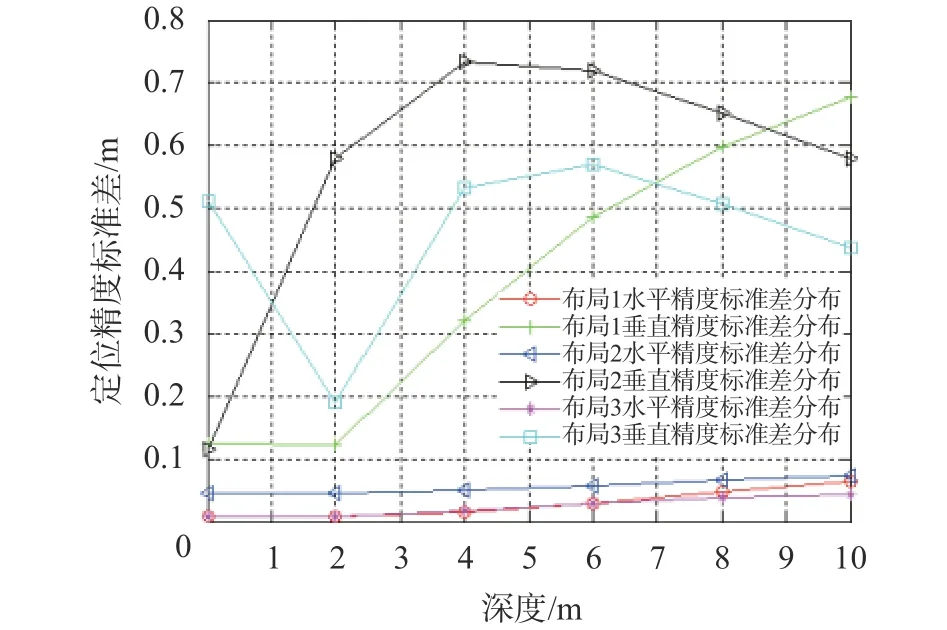
图15 不同布局分层定位精度标准差分布
3 结束语
通过对不同算法、不同节点布局定位精度的仿真,提出炸点精度分布等值线、精度分布平均值、精度分布标准差3个指标对炸点定位系统精度进行评价,能够准确分析炸点定位系统单元对所定位区域的定位效果。其中以精度分布平均值为首要考量因素,再通过精度分布等值线和标准差对方案评估进行补充。通过这一套评估体系,将可以提前对定位算法和基站布局做出选择,以达到提高炸点定位准确度的目的。
