多类型冲击的竞争失效过程可靠性建模研究

刘 鑫，贾云献，李孟涵，周 杰

(1.陆军工程大学石家庄校区，河北 石家庄 050003; 2.军事科学院系统工程研究院，北京 100082;3.河北工业大学，天津 300400)

0 引 言

工程实际中，系统的性能会随时间不断退化最终导致系统失效，即发生退化失效。同时，由于其外部或者内部环境的变化，系统不可避免地会受到各种冲击，如果冲击量超过其承受阈值，会导致系统的突发失效。大部分的系统都同时存在着退化失效和突发失效两种失效模式，最终系统的失效是两种失效模式竞争的结果。例如电阻失效可能是高压击穿、开路或阻值漂移中的一种，前两种失效模式是突发失效，后一种则属于退化失效[1]，最先发生的失效模式造成了电阻的失效，所以电阻的失效是各种失效模式竞争的结果。

竞争失效现象的普遍存在引起了学者们的广泛关注，目前已有许多关于竞争失效模型的研究与应用[2-5]。在理论方面，Kristoffer等[6]研究了竞争失效模式下的疲劳失效机理；Zhang等[7]研究了竞争失效的加速寿命试验方法；Song等[8]研究了多个相互影响的部件所组成的系统的可靠性建模。在应用方面，王海琨等[9]研究了基于竞争失效过程的剩余寿命预测问题；Zhang等[10]研究了基于竞争失效模型的预防性维修的维修决策优化。同时，竞争失效模型在航空发动机[11]，金属化膜脉冲电容器[12]和数控机床[13]等装备或产品的可靠性研究中也得到广泛应用。然而在竞争失效模型研究中，对实际情况进行了大量简化，使得计算结果与系统实际可靠性存在一定差距，在工程中可能会造成可靠度评估偏高而造成损失。基于此，探索一种贴近系统实际工况的竞争失效模型具有重要研究意义。

针对此问题，黄文平等[14]考虑了退化过程对冲击过程的影响，即随着退化量增加，系统抵御冲击能力会下降，导致突发失效阈值产生变化，在此基础上建立了变失效阈值的竞争失效模型。本文在变阈值竞争失效模型的基础上，考虑存在多种不同冲击类型的情况，对竞争失效模型的适用范围进一步扩展。在分析多种冲击类型同时存在时对系统可靠性影响的基础上，结合极值冲击模型给出竞争失效可靠性建模的一般方法。最后，通过某微型发动机的可靠性评估案例，证明该方法的有效性。

1 考虑多类型冲击的竞争失效过程研究

在可靠性研究中，常用冲击模型来表示系统受到的冲击过程[15]，本文以极值冲击模型为例来表示冲击过程。在极值冲击模型中，当某一次冲击量超过预先设定的突发失效阈值时，则认为系统失效。在基于极值冲击模型的竞争失效中，系统退化量Xs(t)由两部分组成，一是系统连续性退化过程，二是系统由于冲击过程所造成的退化量，当二者累积之和超过系统的退化失效阈值H，则系统失效，称为退化失效；或者某一次的冲击量或冲击强度超过突发失效阈值D，系统同样失效，称为突发失效。基于此，竞争失效过程如图1所示，图1（a）中，在系统的退化过程中总共经历了3次冲击过程（冲击量分别为W1、W2和W3，对应退化量Y1、Y2和Y3），且第3次冲击量超过系统阈值，此时，虽然退化量并未达到系统退化失效阈值H，但是系统依然失效，此即为由冲击过程造成的突发失效；图1（b）中，几次冲击均未超过系统阈值，只是造成退化量的增长，最后系统总退化量超过系统退化失效阈值H导致退化失效。

系统在退化过程中，随着退化量增加，其抵御冲击能力会相应降低，所以在系统退化到一定程度且未失效的情况下，其冲击失效阈值应该相应降低。同时，系统在运行过程中会受到多种类型的冲击影响，比如笔记本电脑的电池，其连续性退化过程主要是由于内部化学反应导致充放电能力变弱，而影响电池退化量的冲击过程则包括过热、电压过高等因素。因此，本文在变阈值竞争失效模型基础上研究同时存在两种或者以上不同冲击过程竞争失效模型。假设系统在退化过程中，当总退化量达到某一设定的阈值L（L＜H）时，由于系统抵御外界冲击的能力减弱，突发失效的阈值相应由D1降为D2，此时模型主要有3种失效形式，如图2所示。图2（a）中表示在退化过程中，系统受到两种冲击影响，第一种冲击出现了两次（W1,1和W1,2），第二种冲击出现一次（W2,1），每次冲击的冲击量均未超出最大失效阈值（分别为D1,1和D2,1），最终系统由于总的退化量达到了失效阈值H而失效，并未出现突发失效。图2（b）中，受到同样的冲击过程，虽然系统总退化量远未达到其失效阈值，但是第三次冲击过程超过了失效阈值D2,1而导致系统突发失效。图2（c）中，系统在t0时刻达到了设定的阈值L，此时系统突发失效的阈值变为D1,2和D2,2，接着在t4时刻，由于冲击量超过了阈值D1,2而导致系统突发失效。

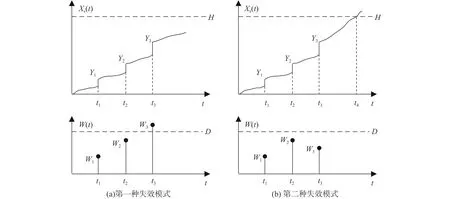
图1 基于极值冲击模型的竞争失效过程

2 系统竞争失效过程的可靠性建模

为建立竞争失效过程的可靠性模型，根据上文分析，需要同时研究系统的退化失效过程和突发失效过程。本文首先建立系统总退化量的退化失效模型，在此基础上，基于变阈值模型，根据突发失效阈值的变化，分两类情况讨论系统竞争失效过程的可靠性建模。

2.1 退化失效模型

对于任何系统的退化失效过程，当总退化量达到失效阈值H时，则认为系统失效。为建立系统退化失效模型，首先需要计算系统总的退化量：

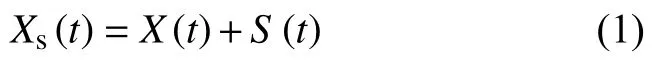
式中：Xs(t)——系统总的退化量；

X(t)——连续退化过程的退化量；

S(t)——冲击过程所造成的退化量。

系统连续性退化过程在工程实际中可能服从任意规律，例如服从Wiener过程或者Gamma过程等，为简化建模过程，假设系统连续性退化过程为线性退化过程，即：

其中，φ表示退化过程的初始退化量，β为退化速率，假设其服从正态分布，即

假设该系统共有l种不同的冲击类型，对于同一类型冲击，所有冲击过程都为到达率λj的泊松过程。每次冲击过程造成的退化量为Yj,k（第j种冲击类型第k次出现），且假设冲击量为服从正态分布的独立同分布非负随机变量，即此时，外界冲击所造成的退化量为：

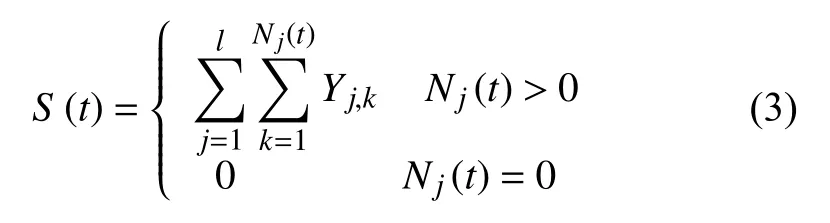
其中Nj(t)为第j种冲击类型出现的次数。

综合以上分析，系统不发生退化失效的概率为：

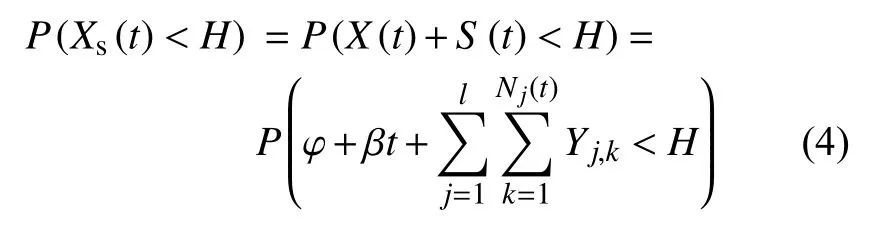
根据条件概率的性质，可以将其表示为：

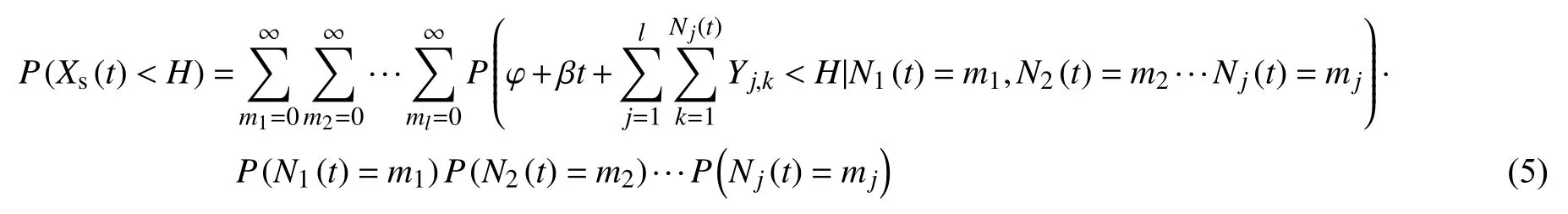
由于已经假设冲击的退化量服从正态分布，冲击过程服从泊松分布，则可以计算系统不发生退化失效的概率为：

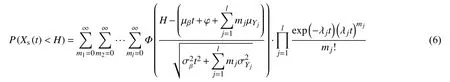
2.2 竞争失效可靠性建模

在竞争失效模型中，需要在连续性退化过程中同时考虑突发失效，在本文中即冲击过程。假设Wj,k（第j种冲击类型第k次的冲击量）为冲击量的大小，且服从独立同分布的正态分布则系统不发生突发失效概率为：

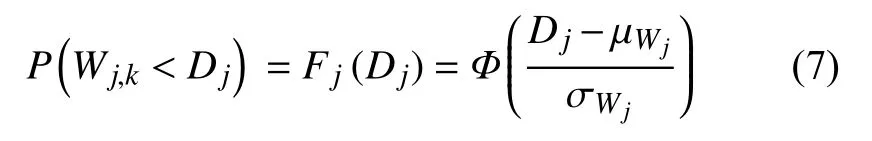
在变失效阈值的情况下，同时考虑多种冲击类型的存在，系统的可靠性建模十分复杂，因此，根据失效阈值的变化将竞争失效过程的可靠性计算分为两种情况讨论。

1）系统的性能退化总量小于L，即突发失效的阈值为Dj,1，此时系统的可靠度函数即为总退化量小于L，且每种类型的冲击每次出现时的冲击量都小于突发失效阈值Dj,1的概率。根据前面的计算，可以得到：

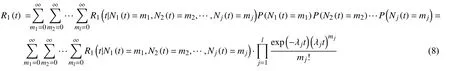
最后得到可靠度为：

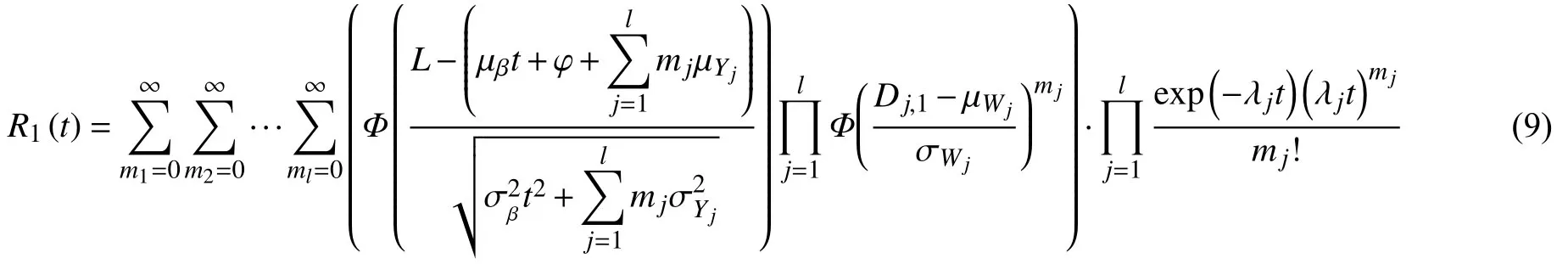
2）系统的退化量大于或者等于L且小于H，此时系统的可靠性函数为：

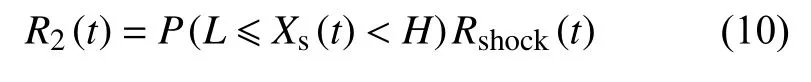
其中Rshock(t)为在冲击影响下系统不发生冲击失效的可靠度函数。假设系统共经历各种冲击过程n=次，且u(u＜t)为退化量到达L的时刻。令pj为[0,u]上第j类冲击发生的次数，qj为(u,t)上第j类冲击发生的次数，且根据泊松过程的性质，满足上面情况的概率为：

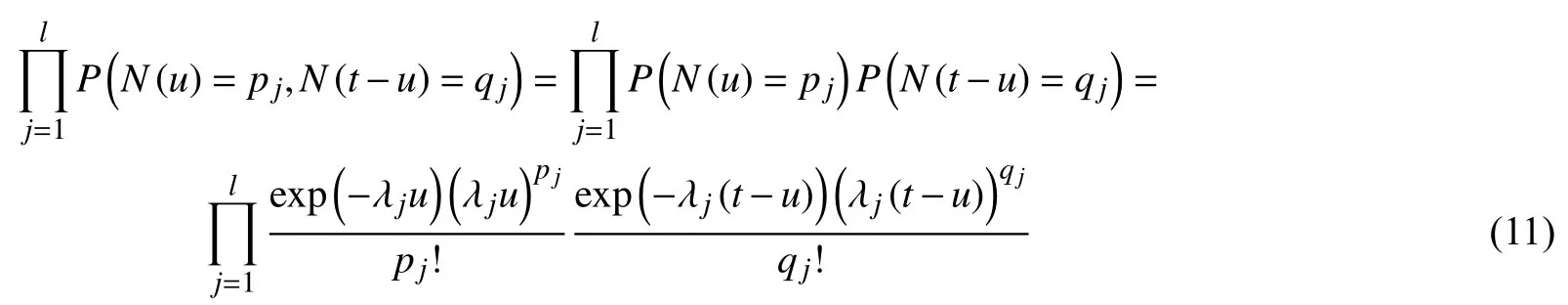
令FX(N(u),L,u)为系统退化量小于L且外界冲击总数为时不发生失效的分布函数：

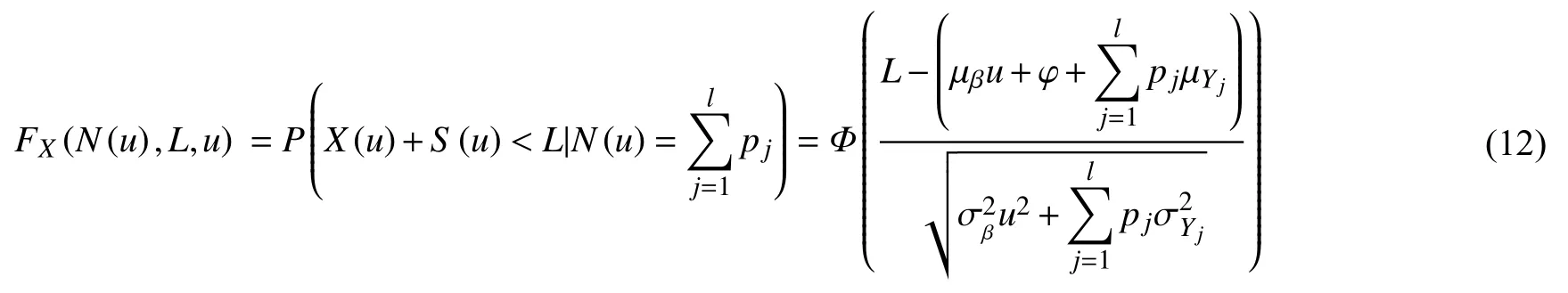
对t求导数，可以得到其密度函数为：

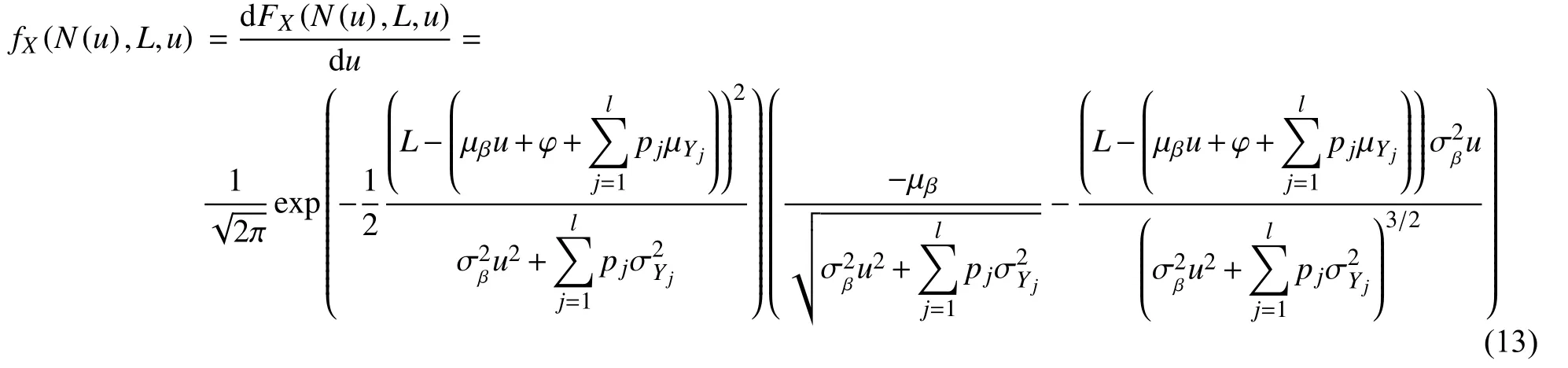
综合以上分析，可以得到其可靠性为：

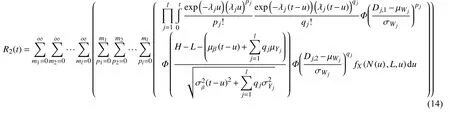
其中pj+qj=mj,∀j。

因为此两种状态为互斥事件，因此可靠度为二者之和，即：

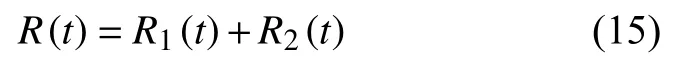
为了对所建立的可靠性模型进行验证，选取冲击次数为0这一特例进行检验。此时m1=m2=···=mj=0，即不存在任何冲击过程，此时的模型应该为变失效阈值的竞争失效模型。将其带入建立的可靠性模型中，可以得到：

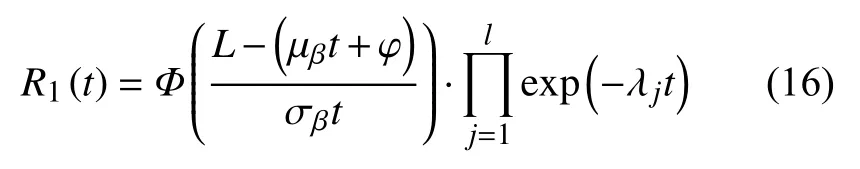
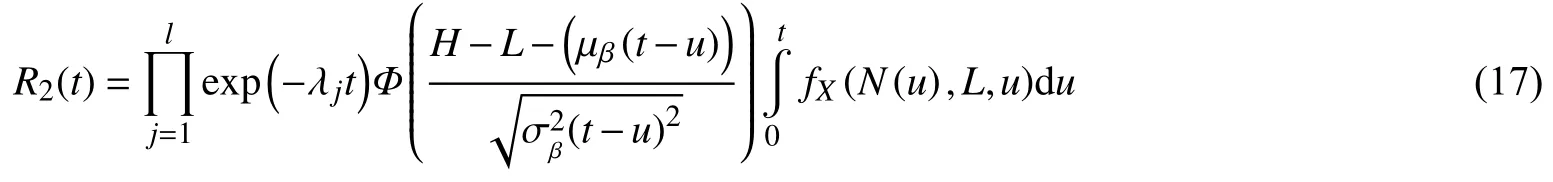
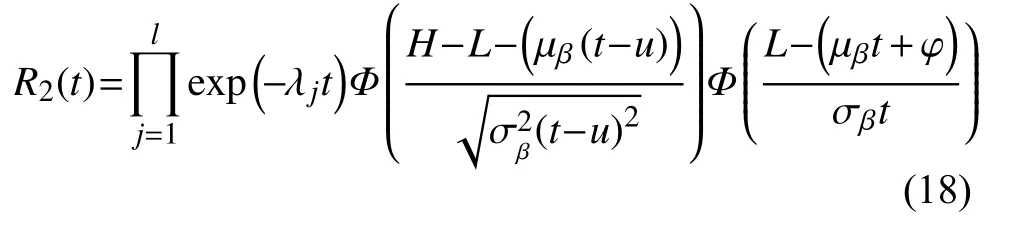
此时，可以得到系统的可靠度为：

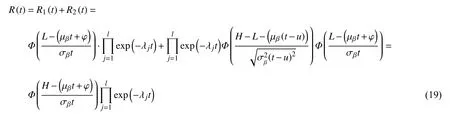
此结果与文献[14]的模型在形式上是一致的，而区别在于不发生外界冲击的概率是不同的，造成这一结果的原因是本文的模型考虑了多种类型的冲击同时存在的情况。

3 案例分析

本文选取桑迪亚国家实验室某微型发动机为研究对象，对所建立的模型进行验证。该微型发动机在运行过程中同时存在着磨损退化与冲击过程，由摩擦造成的磨损退化是微型发动机失效的主要模式，同时冲击会产生一定量的磨损碎屑，当冲击量大于一定阈值时也会导致其失效。该微型发动机的失效过程同时包括连续退化过程和冲击过程，为典型的竞争失效过程。微型发动机的数据主要来自文献[16]，为了对本文的模型进行验证，在原有数据基础上，假设第二种冲击类型的存在，为了简化计算，假设只存在两种类型的冲击过程，且两种冲击类型服从到达率相同的泊松分布，同时对微型发动机的变失效阈值进行假设，其主要参数如表1所示。

根据本文提出的考虑多种冲击类型的竞争失效可靠性模型，计算微型发动机的可靠度函数如图3所示。可以看到，在20 000转之前，发动机的可靠度下降相对缓慢，仍然保持较高的可靠度水平，在50 000转左右，发动机的可靠度急剧下降，这主要是由于系统退化量达到变阈值水平，发动机抵御外界冲击的能力变弱，失效阈值降低，所以可靠度迅速下降，在75 000转之后，发动机性能又相对平稳，可靠度下降又相对缓慢。文献[14]中的模型只考虑了变阈值，没有考虑存在多种冲击类型的情况，且由于本案例中第二类冲击造成的退化量比第一类要大，导致其各个时刻的可靠度评估结果都比本文模型的结果高。

为更清楚地进行对比，二者相同时刻可靠度差值如图4所示，可以看到，可靠度差值随时间迅速增大，然后又逐渐减小，差值在45 000~55 000转达到最大，主要原因和上文中分析相同，为发动机退化量达到规定阈值，导致冲击阈值下降，由于本文模型假设存在两种冲击类型，且第二类冲击造成的冲击量均值比第一种要大，所以退化量会首先到达变阈值临界点，导致发动机可靠度迅速下降。本文模型由于综合考虑了多种因素的影响，与系统真实的工作环境更加接近，得到的可靠度结果也更为全面，可以有效避免对可靠性的过高估计而带来的损失。

表1 某微型发动机竞争失效过程参数

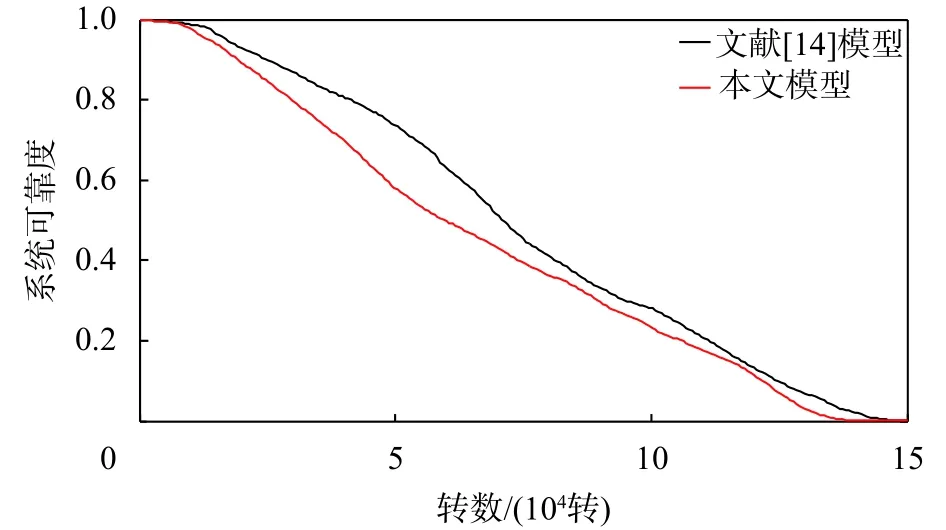
图3 微型发动机寿命可靠度函数

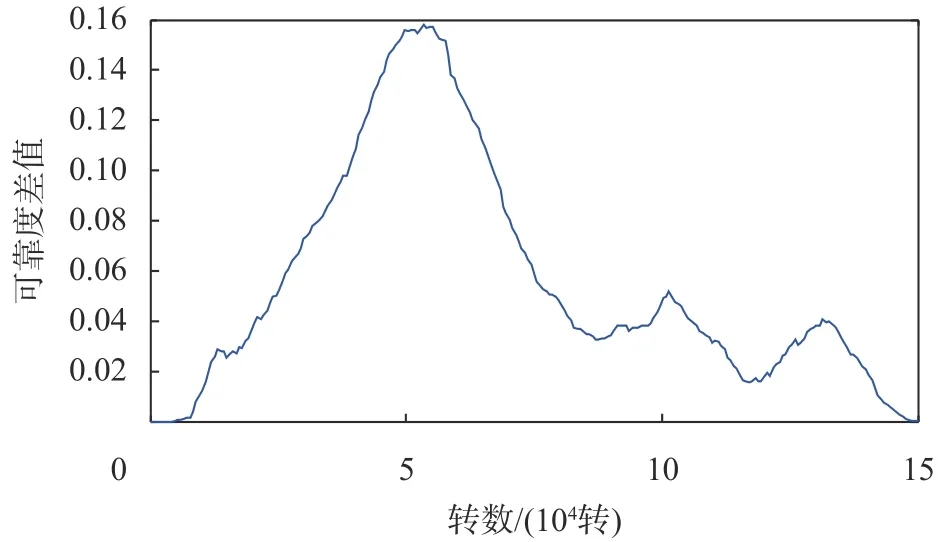
图4 基于不同模型的可靠度差值

4 结束语

本文针对竞争失效模型连续性退化过程中同时存在多种类型冲击问题，在变阈值竞争失效模型基础上，研究了系统可靠性建模。首先，研究了基于极值冲击模型的竞争失效，在此基础上，分析了多种冲击类型同时存在时对系统可靠性的影响，给出了竞争失效模型主要失效模式；最后，建立了该模型的解析表达式。主要结论如下：1）本文建立的可靠性模型，减少了理想化条件，提高了模型的适用性和合理性；2）考虑存在多种类型冲击存在的情况，可以得到更为全面的评估结果，提高了可靠性评估精度，避免了对系统可靠性的乐观估计；3）以某微型发动机为研究对象，验证了该模型的有效性，具有一定的工程应用和推广价值。

本文在竞争失效的可靠性建模中，因为建模过程十分复杂，为简化计算，均假设装备寿命服从正态分布。因此，如何建立适用范围广，适合各种系统的竞争失效可靠性模型，值得进一步探索研究。