黄河下游河道输沙沿程调整变化模拟

张启照

（郑州财经学院土木工程学院，河南 郑州450000）

黄河下游河道泥沙输移具有“多来多排多淤”的特点，输沙率常采用考虑上站来水含沙量的经验公式QS=KSa0Qb（QS为输沙率，Q、S0分别为流量、上站来水含沙量，K为输沙系数，a、b分别为输沙指数）表示[1]。其中，系数K与指数a、b是3个重要的待定参数，用于反映输沙能力在时间、空间上随河床边界条件的变化。输沙系数K主要与河床累计冲淤量有关[2-4]，当河道发生累计淤积时K值增大，当河道发生累计冲刷时K值减小；输沙指数a、b主要与河床边界几何形态条件有关，如河相系数B0.5/H（B为河宽，H为水深）、比降J等[5-6]。

输沙率经验公式结构简单、方便实用，在黄河下游河道输沙计算中得到了广泛应用[7-8]。不过，该公式也存在以下不足之处：①作为一种经验公式，缺乏理论基础；②不同河段的K、a、b变化范围较大，需要通过实测资料进行率定，缺少可靠的计算方法，现有关于K、a、b变化规律进的研究尚多处于经验阶段。

经验公式的完善往往需以与理论公式的比较研究为基础。通过比较输沙率经验公式与不平衡输沙理论方程[9-12]的区别与联系，从理论上研究指数a、b的变化规律，最终可以构建出一种变幂指数的泥沙输移模型[13]。本文简要介绍了泥沙输移变幂指数模型的建立过程，并结合黄河下游河道实测水沙数据，重点对花园口—高村（游荡型）、艾山—利津（弯曲型）段输沙沿程调整变化进行模拟计算。

1 冲积河流泥沙输移变幂指数模型

在恒定流情况下，QS=KSa0Qb可以进一步表示为断面含沙量形式：

当S0等于水流挟沙能力S*时，河道处于输沙平衡状态，有S0=S*=S，代入式（1）可得S*与Q之间的幂函数形式：

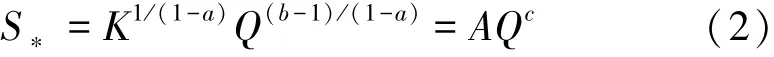
式中：A为挟沙力系数；c为指数。

基于式（2），式（1）可以进一步表示为

对于式（3），假设指数a沿程呈指数衰减，即：a=e-κx（κ为待定参数；x为纵向沿程距进口断面距离，x=0，a=1.0，S=S0；x→∞，a→0，S→S*）。 则式（3）对应的微分方程为

一维不平衡输沙理论微分方程[10]为

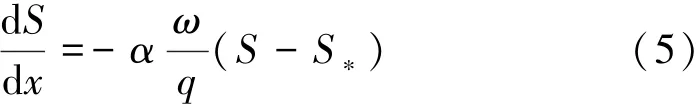
式中：ω为泥沙沉速；q为单宽流量；α为泥沙恢复饱和系数。

因此有

相应式（3）中指数a计算公式为

结合式（2）、式（3）与式（8），共同构成了一种变幂指数的泥沙输移模型[13]，转化为输沙率形式：

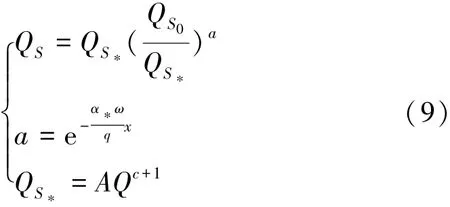
式中：QS=QS；QS0为上站来沙率，QS0=QS0；QS*为水流输沙能力，QS*=QS*。

2 黄河下游水沙沿程调整资料

2.1 下游河道基本概况

黄河下游河道西起河南省郑州市桃花峪，东至山东省东营市利津县，流经河南、山东两省，全长约786 km，落差93.6 m，平均比降0.012%，沿程分布有花园口、高村、孙口、艾山、泺口、利津等水文站。黄河下游河道按照平面形态不同可以划分为3段：上段自桃花峪至高村，为游荡型河段；中段自高村至陶城铺，为从游荡型到弯曲型的过渡河段；下段自陶城铺至利津，为较为稳定的弯曲型河段。其中：游荡型河段中的花园口—高村段全长约177.9 km，弯曲型河段中的艾山—利津段全长约269.6 km。黄河下游沿程不同的典型过水断面不同年份的水力几何形态关系见表1[14-15]。单宽流量作为水深与流速的乘积，其与流量之间也相应呈幂函数关系。不过，幂函数系数、指数随断面、年份不同而有所差别。

表1 黄河下游河道典型断面水力几何形态关系

2.2 水沙沿程调整分析

图1为黄河下游河道花园口、高村、艾山、利津水文站1952—2010年实测年均水沙资料（图中三门峡、龙羊峡、小浪底对应时间为这3座水库建成时间）。可以看出，近些年来受气候变化、水库调蓄、人类用水等多方面的影响，黄河下游各站来水来沙总体均出现明显的下降趋势。特别是20世纪90年代后，各站年均流量多小于1 000 m3/s。受不同河段挟沙能力差别以及输沙沿程调整影响，花园口—高村段出口含沙量多低于进口含沙量；艾山—利津段在20世纪70年代中期以前出口站含沙量相比进口站含沙量有大有小，基本处于输沙平衡状态，70年代中期以后出口含沙量多低于进口含沙量。

图1 黄河下游河道水沙沿程调整变化情况

3 黄河下游输沙沿程变化模拟

基于式（9）分别对黄河下游花园口—高村（游荡型）、艾山—利津（弯曲型）段1952—2010年年均输沙率沿程调整变化情况进行模拟计算。其中，花园口—高村、艾山—利津段悬沙多年平均粒径约为0.018 mm，泥沙恢复饱和系数α取0.01；对于单宽流量q，根据表1中相关断面水力几何形态关系推求（1986年前采用1985年断面水力几何形态关系，1986年后采用2011年断面水力几何形态关系）；关于水流输沙能力QS*，参考相关文献半理论半经验推导结果[16]，并分别基于花园口—高村、艾山—利津段实测水沙资料，认为当进、出口断面输沙率QS差值百分比在10%以内时，近似认为河道处于冲淤平衡状态，通过拟合率定确定（见图 2）：

式中：QS*花-高、QS*艾-利分别为花园口—高村与艾山—利津河段水流输沙能力，t/s；Q高、Q利分别为高村与利津站年平均流量，m3/s。

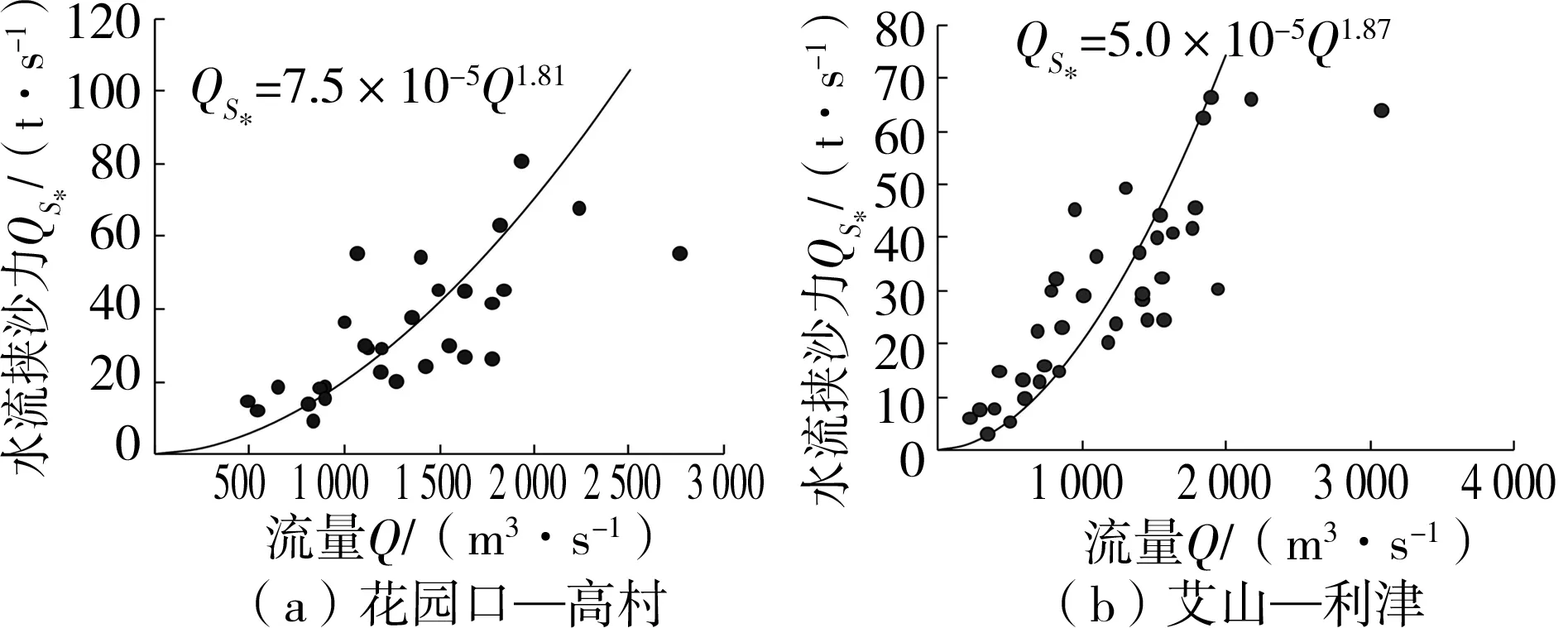
图2 不同河段水流挟沙力与流量的关系

图3 分别为黄河下游花园口—高村、艾山—利津段出口站年均输沙率模拟结果。可以看出：花园口—高村、艾山—利津段出口站计算值与实测值基本一致，确定系数R2均大于0.97。

图3 黄河下游河道年均输沙率计算值与实测值比较

4 结 论

（1）通过比较输沙率经验公式QS=KSa0Qb与不平衡输沙理论方程之间的区别与联系，理论推导研究了经验公式指数的变化规律，提出构建了一种变幂指数的泥沙输移模型。

（2）应用泥沙输移变幂指数模型，分别对黄河下游花园口—高村与艾山—利津段输沙沿程调整变化进行模拟计算。结果表明，计算值与实测值基本一致，确定系数R2均大于0.97。