A CFD-based numerical virtual flight simulator and its application in control law design of a maneuverable missile model
2020-01-09LaipingZHANGXinghuaCHANGRongMAZhongZHAONianhuaWANG
Laiping ZHANG, Xinghua CHANG, Rong MA, Zhong ZHAO,Nianhua WANG
a State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
b Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
Abstract A CFD-based Numerical Virtual Flight (NVF) simulator is presented, which integrates an unsteady flow solver on moving hybrid grids,a Rigid-Body Dynamics(RBD)solver and a module of the Flight Control System (FCS). A technique of dynamic hybrid grids is developed to control the active control surfaces with body morphing, with a technique of parallel unstructured dynamic overlapping grids generating proper moving grids over the deflecting control surfaces(e.g. the afterbody rudders of a missile). For the flow/kinematic coupled problems, the 6 Degree-Of-Freedom (DOF) equations are solved by an explicit or implicit method coupled with the URANS CFD solver. The module of the control law is explicitly coupled into the NVF simulator and then improved by the simulation of the pitching maneuver process of a maneuverable missile model.A nonlinear dynamic inversion method is then implemented to design the control law for the pitching process of the maneuverable missile model. Simulations and analysis of the pitching maneuver process are carried out by the NVF simulator to improve the flight control law. Higher control response performance is obtained by adjusting the gain factors and adding an integrator into the control loop.
KEYWORDS Dynamic hybrid grid generation;Flight control law;Flow/kinematic coupling method;Maneuverable missile pitching;Nonlinear dynamic inversion;Numerical virtual flight
1. Introduction
In recent years, increasing demands for maneuverability and agility require superior performance of aerospace vehicles under unsteady conditions and higher-quality flight control systems. The flight envelops of the next generation aircraft are becoming wider and wider;the aerodynamic characteristics exceed the linear interval,so the traditional control laws based on the linear assumption with small perturbations are no longer suitable. In addition, the next generation aircraft will have much higher maneuvering performance, resulting in stronger unsteady effects, and the strong coupling of aerodynamics and kinematics, as well as the flight control law and even structural dynamics(aero-elastics).To solve these complicated and strongly coupled multi-physics problems, virtual flight experimental technologies1-4have been developed. The rapid development of computer science and numerical methods leads to growing attention to various CFD-based multiphysics simulation methods. These methods aim at predicting closed-loop response characteristics during a maneuvering flight via numerical simulations, known as the Numerical Virtual Flight (NVF) or digital flight.5
The past two decades have witnessed the development of integrated software systems of the numerical simulation, virtual flight and optimization in many programs, such as the AVT-161 program of the Research Treaty Organization,6the SikMa (Simulation of Complex Maneuvers) program,7the Digital-X program8,9of DLR,and the CREATE(Computational Research and Engineering Acquisition Tools and Environment) Program10,11of the DoD HPCMP in America.In the CREATE-AV (aero-vehicle) sub-program, a 12-year long-term program since 2008, two multi-physics simulation systems, Kestrel12,13and Helios14,15, were developed for the fixed-wing aircraft and helicopters,respectively.The main goal of Kestrel and Helios is to develop necessary virtual flight simulation tools for the next generation aircraft. Some exciting results by these coupled solvers have been reported in a series of papers.
Using the NVF tools, engineers can evaluate and further improve the flight control law for fast maneuvering flights,resulting in revolution and innovation of aircraft design patterns from the traditional ‘‘fly and fix” mode to the integrated multi-discipline design mode.1,16Even in the initial concept design phase, the effects of the flight control system can be considered to avoid the risks of subsequent flight tests, and to further improve and optimize the design of aerodynamic configurations and the flight control system in the detailed design phase.1,5
In fact, the CFD/ Rigid-Body Dynamics (RBD) coupled methods have been studied continuously in the academic community for the last two decades, focusing on coupled approaches and flight stability analysis. For example, Zhang et al. studied the dynamic stability performance of a reentry capsule17,18and a rocking delta wing19; Yang et al. simulated the roll and sideslip coupling motions of a slender delta wing20;Sahu carried out a time-accurate numerical prediction of freeflight aerodynamics of a finned projectile.21However, most previous works did not consider the response of the control law. In recent years, some preliminary studies considering the dynamic response of vehicles by an open- or closed-loop control law have been reported. For instance, Wang et al.developed a CFD/RBD coupled solver on dynamic overlapping structured grids and simulated the pitching maneuver of a missile with strake wings22; Xi et al. presented coupled CFD/RBD modeling for a finned projectile with control,using overlapping structured grids23; Chen et al. coupled a Proportion-Integral-Derivative (PID) controller into their CFD/RBD coupled solver on moving structured grids24;Allan et al. studied the longitudinal flight mechanics with control based on a structured CFD solver.25However,the NVF simulation of a realistic vehicle with complicated geometry is still a difficult task, or even a grand challenge.5,8,10
For a CFD/RBD/ Flight Control System (FCS) coupled NVF system, three key issues should be considered: the dynamic mesh generation,unsteady flow simulation,and multidisciplinary coupling method.Based on the authors’previous work,26-29a CFD-based NVF simulator is presented here,which integrates an unsteady flow solver on moving hybrid grids,a rigid-body dynamics solver,and a module of the flight control system.This simulator is then applied in the simulation of the pitching maneuver process of a maneuverable missile model to improve the control law.A dynamic hybrid grid technique is developed to investigate the active control surfaces with body morphing. A parallel unstructured dynamic overlapping grid technique is adopted to generate proper moving grids on the deflecting control surfaces(e.g.the afterbody rudders of a missile),while the body or the control surface morphing is controlled by a Radius Basis Function (RBF) based interpolation or other morphing grid approaches. The unsteady flow field is simulated by a parallel URANS solver based on the second-order cell-centered finite volume method.For the flow/kinematic coupled problems, the 6 Degree-Of-Freedom(DOF)equations are solved by an explicit or implicit method coupled with the URANS CFD solver.The module of the control law is explicitly coupled into the NVF simulator.Due to the strong nonlinear effects of the missile model at high angles of attack and strong hysteresis effects caused by highspeed maneuvering, the traditional linear control law is no longer suitable.Hence,we adopt the nonlinear dynamic inversion method,30instead of the widely-used PID control approach,24,31to design the control law. The pitching process of the model with an input control command (the angle of attack pitching-up from 0° to 30°) is simulated by the NVF simulator, and the influences of control parameters are analyzed. Higher control performance is obtained by adjusting the gain factors and adding an integrator into the control loop.
2. Numerical methods of CFD-based NVF simulator
2.1.Main procedure of CFD/RBD/FCS coupled NVF simulator
As discussed in Section 1, in order to simulate aerodynamics/kinematics/flight-control coupled problems, a multi-physics integrated solver should be first set up, in which the modules of dynamic grid generation, the unsteady flow simulation,the computation of 6-DOF equations and the flight control law should be coupled within a unified framework.
Here, we develop a CFD/RBD/FCS coupled NVF simulator as shown in Fig. 1. The procedure can be described as follows:
(1) The program starts with the initial unstructured grid generation. If the overlapping grid approach is adopted to deal with different parts of the flow field, a parallel implicit hole-cutting will be carried out to assemble the overlapping grids.32
(2) The initial steady flow field is simulated by the URANS solver26,27and then the aerodynamic forces are obtained for the initial steady state ((n=0)th step).

Fig.1 Flow chart of CFD/RBD/FCS coupled NVF simulator.
(3) Substitute the aerodynamic forces into the 6-DOF flight dynamics solver to obtain the 6-DOF information of the next time step ((n+1)th step).
(4) Input aerodynamic forces and the 6-DOF information of the vehicle to the flight control law module to obtain the deflection of the control surfaces of the (n+1)th time step.
(5) Generate the moving grids according to the 6-DOF information of the vehicle and the control surfaces at the (n+1)th time step.
(6) Simulate the unsteady flow field and calculate the aerodynamic forces at the (n+1)th time step by the URANS solver.
(7) Repeat Steps (1)-(6) until the goal time.In the following sub-sections, we will discuss the details of some main modules and the implementation of module integration.
2.2. Technique for generating dynamic hybrid grids
Since grid generation is the first step for CFD simulation, the grid quality directly influences the accuracy of numerical results, especially for complex configurations.33For a realistic maneuver vehicle,dynamic grids should be generated automatically during maneuvering. The level of grid generation automation is directly relative to the efficiency of maneuvering flight simulation. To deal with the deflection of control surfaces during maneuvering flights, the overlapping grid technique or the sliding grid technique should be a preferred choice.However,for the problems with a morphing body,such as fish schooling and aero-elastic wings, the morphing grid techniques should be adopted. We thus integrate all the moving grid techniques into our dynamic grid generator based on our previous work.26-28
In order to integrate the moving grid techniques within a grid generator as independent modules, a kinematic and computational domain decomposition approach is developed as shown in Fig. 2. For example, the multi-body kinematics can be decomposed into the translation of the gravity center of each body in the inertial ground coordinate system, while the body is morphed and rotated in its own body-fixed coordinate system. Then the computational domain can be decomposed into several zones: the background grid zone (Zone 0), the active deforming zones and the passive deforming zones around each body.Some zones of each body may overlap with each other(e.g.Zone 1.2 and Zone 2.2 in Fig.2),or Zones 1-3 may overlap with the background grid zone (Zone 0) as in Refs.12-15. For these cases, the overlapping grid technique is adopted. In addition, for each body in Fig. 2 (whether it is an active deforming zone or a passive deforming zone), some morphing grid techniques (such as spring analogy, Delaunay background grid mapping or RBF interpolation), and the remeshing technique if needed, can be used to generate proper moving grids with high efficiency. The procedure of our dynamic grid generator is illustrated in Fig. 3.

Fig.2 Strategy of multi-body kinematic and computational domain decomposition.
Next, we will demonstrate the ability of our dynamic grid generator with two cases. The first is two-dimensional fish schooling. The body of a fish is simulated by NACA0012 airfoil, and the locomotion of the body is the same as that in Ref.34. Four-fish schooling is considered, and the dynamic hybrid grids at four typical time steps are presented, as shown in Fig.4.It can be seen that the present dynamic grid generator can generate high-quality grids for this case with the morphing body and overlapping multi-zones.
In the second case, a maneuverable missile model is examined, as shown in Fig. 5. The afterbody rudders deflect simultaneously by the same angle during the pitching process in an‘x’-type layout. Fig. 6 shows the initial hybrid grids. The total number of the cells of the half model is about 17.0 M, including 13.9 M over the body, and 1.55 M for each rudder with prisms in the boundary layer and tetrahedral cells in the offbody region. The initial hole-cutting results are shown in

Fig.3 Procedure of dynamic hybrid grid generation.

Fig.4 Dynamic hybrid grids for four-fish schooling at four typical time steps.

Fig.5 Configuration of maneuvering missile model.
Fig.7(a). During the pitching process, the dynamic overlapping grids over the afterbody rudders at some typical states are shown in Fig.7(b)-(f), while the grids over the body are rotated with the pitching angles using a rigid body-fixed approach for simplicity. In the parallel environment with 256 CPUs (1.5 GHz FT1500A processor), only about 20 s are needed for each step of the hole-cutting assembling (2% of the time of unsteady flow simulation).
2.3. Unsteady flow solver on dynamic hybrid grids

Fig.6 Initial grids over missile model.

Fig.7 Dynamic overlapping grids over deflecting rudders during pitching.
The unsteady flow solver is based on the well-known cellcentered second-order finite volume discretization of the URANS equations in an Arbitrary-Lagrange-Eulerian (ALE)framework.In the steady-state cases of moving grids,the block LU-SGS implicit method is adopted for temporal advancing,and in the unsteady cases, the well-known dual-time stepping approach is utilized.More details can be found in our previous work.26-29To improve the accuracy of unsteady flow simulations, the Geometry Conservation Law (GCL) on moving grids was investigated in Ref.29. Some verification and validation test cases have been shown in Refs.26-29,which will not be repeated here.
2.4. Coupling strategy: loose coupling and strong coupling
For aerodynamics/kinematics/flight-control coupled problems,the right-hand terms of URANS equations and the 6-DOF governing equations are related to both the flow variables and the kinematics variables; therefore, the governing equations for the coupled system proposed can be written as

where E is the flow variable and F the 6-DOF variable. Two types of methods for Eq. (1) can be used: the monolithic method and the partitioned one. The former solves the system simultaneously within one global system, but is seldom used for CFD/RBD coupled problems due to its complicated implementation. Here we adopt the partitioned method,35in which the two groups of governing equations are solved separately and the information exchange between them is needed in each time marching step.
In the partitioned method, loose or strong coupling (fully implicit)approaches36can be used based on the time marching method for the two groups of equations.In the loose coupling approach,the 6-DOF system is advanced explicitly;thus,there always exists an obvious lag between the information of the subsystems in time advancing, which may result in instability sometimes. In the strong coupling approach, an implicit scheme is adopted to solve the 6-DOF system,and the coupled system is iteratively solved in a time step to get a convergence solution.
Both the loose and strong coupling strategies have been integrated into our NVF solver. Note that the flight control law is coupled in an explicit manner. For each real-time step,the command from the flight control law will be updated according to the current kinematic parameters, and then the control law outputs the deflection of control surfaces to the next time step. In the next section, we will discuss the control law design approach in detail.
2.5. Implementation of module integration
In order to integrate all these modules, as well as other multiphysics modules in the future, into the NVF simulator, an object-oriented integration framework is developed, which is similar to that in Refs.12,13. The architecture is a modular approach factoring traditional monolithic solvers into the framework, including components to perform fluid dynamics,kinematics and kinetics, flight control and other analysis.Fig. 8 depicts a notional view of the software architecture.The infrastructure and executive is an event-driven infrastructure that is component unaware. The components themselves can produce or respond to events and subscribe to or publish data;thus,the infrastructure and executive can be coded once,and the eXtensible Markup Language (XML) input file can specify the use case and contributing components.
Fig.8 shows two big dashed boxes surrounding the components. The left-hand box denotes the components that are the shared objects with the framework,maintained by the authors’team. The right-hand box represents executables from outside sources that will exchange data via an executable-to-executable communication path. This feature will be implemented in the later versions, allowing industries or commodity software to work with the NVF simulator without significant rewrites of their software. An example use incorporates a ‘‘black box”auto-pilot from other contractors into the simulation.
As shown in Fig. 8, all the modules discussed in the previous sub-sections have been integrated into the framework.Some other modules,small dashed boxes in the‘‘internal components” box, will be integrated in the future, such as a highorder DG/FV flow solver, a finite-element structural solver,and a modal structural solver. Then we can deal with CFD/CSD/RBD/FCS coupled problems.
3. Application of NVF simulator: pitching simulation of a maneuverable missile model
We use the NVF simulator presented in Section 2 to simulate the rapid pitching process of the maneuverable missile model(Fig. 5) and to improve the control law by adjusting the gain factors. The specific goals of the flight control law are: (A)to reduce or even eliminate the static error to improve the control accuracy; (B) to control the overshoot phenomenon to decrease large structural overloads;(C) to reduce the response time and thus to improve agility.
3.1. Design of nonlinear dynamic inversion control law
The pitching process for the maneuverable missile model presents strong nonlinear characteristics at a high angle of attack,which may also result in a strong unsteady hysteresis effect,so the nonlinear dynamic inversion method is adopted to design the control law in this work. An affine nonlinear system can be described by the following equation:

where x is a state variable,υ is the derivative of x with time t,u is the target control variable, and f and G are some control transfer functions.
The state feedback method can be described as follows:If G(x) is invertible, then

Thus the system can be reduced to a linear dynamic system as follows:


Fig.8 Architectural design of NVF simulator.
For a given signal xc(t),the error between the actual state x(t)and xc(t)is taken as the input of the linearized system.Thus,the signal can be tracked.
For the pitching of the maneuverable model,the time-scale separation technique is adopted in designing the dynamic inversion control law.The kinematics equations are considered as the slow loop (outer loop), while the kinetic equations the fast loop (inner loop). To design the slow loop control law,the impact of the fast variables is ignored;and for the fast loop control law, the slow variables are considered approximately constant.
For the outer loop, we introduce the kinematics equations into Eq. (2), and rewrite them into the form of Eq. (2). Then we have

in which α is the angle of attack, and q is the pitching angular velocity. Eq. (5) can be further written as

According to Eq. (4), the slow loop control law can be obtained as follows:

where qcis the command angular velocity, and kαis the gain factor for the slow loop control.
Then the inner loop is designed. Here the influences of the dynamic derivative terms are ignored because dynamic derivative terms generally play a damping role, affecting only the response process with little effect on the final steady-state results. Meanwhile, the cost of calculating dynamic derivative terms by the unsteady CFD method is relatively high; therefore, the aerodynamic model of the missile pitching channel can be simplified as follows:

in which mais the pitching moment, Q=ρu2/2 is the inflow dynamic pressure,ρ is the inflow density,u is the inflow velocity, S is the reference area, c is the reference length, and Cmis the static pitching moment coefficient, which is a function of the angle of attack α and the rudder deflection angle δ.Assume that the pitching moment coefficient is approximately linear with the rudder deflection angle, i.e.:

Cmδ(α ) is the derivative of the pitching moment with respect to the deflecting angle of the rudder at δ=0°. These two quantities are related only to the angle of attack α and can be obtained by linear interpolation from the static aerodynamic database. Therefore, the kinetic equation of the fast loop can be written as
in which I is the inertia of the pitching channel. Similar to the slow loop design, the fast loop control law can obtain the following equation:
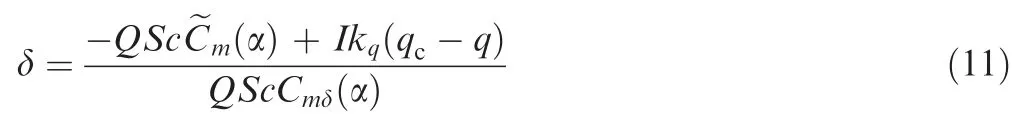
where kqis the gain factor of the fast loop control.
Due to the approximation between the aerodynamic model and the actual plant, the aerodynamic moment formed by the rudder deflection according to Eqs.(7)and(11)is often different from the expected command value.Therefore,a static error(ess=α - αc) usually exists between the steady-state value of the angle of attack α and the command one αc.The static error can be reduced by increasing the gain factor to some extent,but cannot be completely eliminated. An integrator is thus introduced to the slow loop to reduce the static error:
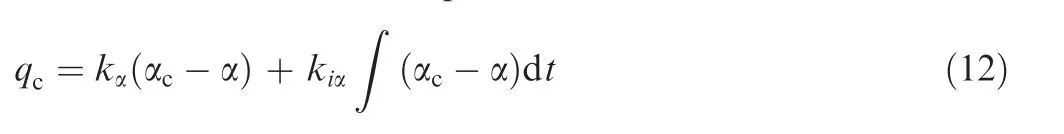
where kiαis the integrating gain factor.
In engineering applications, some physical limitations,such as the maximum rudder angle δ|Limit, and the maximum rudder deflection angular velocity ωδ|Limit, should be added to flight control devices. These nonlinear physical limitations may lead to divergence of the control system; therefore,restricting the contribution of the integrator and the command angular velocity in the control law is necessary to enhance the stability and to improve the dynamic response capability of the system. The flight control system, illustrated in Fig. 9, is a simplified model, reflecting the real flight control of a missile with one channel (pitching) considered and without the consideration of the steering actuator. The command interval is set to 2.5 ms, close to the actual parameter of drive actuators.

Fig.9 Sketch of flight control system.
3.2. Static aerodynamic characteristics
The inflow Mach number Ma is 0.6 and the Reynolds number based on 1 m is 2×106.The well-known SA turbulence model is adopted in the following simulations. The inflow temperature is set to 288.15 K according to the wind tunnel experimental environment. The reference length is taken as the model diameter d=0.16002 m, and the reference area S is πd2/4=0.020111 m2. The moment reference point (xc, yc, zc)is (9d, 0d, 0d)=(1.44018 m, 0 m, 0 m), and the moment of inertia of the pitching channel I is 127.0 kg·m3.
A half model is adopted to save computational costs since only the pitching process is considered in this study.The computational hybrid overlapping grids are shown in Figs.6 and 7.The coordinate system here is generally used in flight mechanics,in which the x-axis is in the plumb symmetry plane,parallel to the model design axis to the head,the y-axis is perpendicular to the plumb symmetry plane to the right of the missile body,and the z-axis is in the plumb symmetry plane, perpendicular to the x-y plane pointing to the earth. In this coordinate system, the pitching-up moment and the upward deflection of the rudder leading edge are defined as positive values.
The pitching moment coefficients for different angles of attack and rudder deflection angles are shown in Table 1 and Fig.10.In Table 1,the trimmed deflection angle of the rudder δcis identified as -10.284° for the expected pitching angle of attack(αc=30°).The derivatives of the pitching moment with respect to the deflecting angle of the rudder (δ=0°) can be derived from the values of the pitching moment coefficients(see the last column in Table 1). It can be seen that the model is basically statically stable in the concerned range(-5°<α <45°), and the pitching moment is relatively linear when both the rudder deflections and the angles of attack are small. However, in the cases of higher angles of attack or larger rudder deflections, nonlinearity appears, and the model becomes statically unstable. In these situations, it is difficult to design the control law by the traditional linear method.
3.3. Typical cases with different gain factors
For the unsteady cases, the simulations start from the converged steady state at the angle of attack 0°.In order to ensure convergence in each real-time step,the total pseudo-time steps of sub-iterations are set to 100. The job stops when the real physical time reaches 2 s for each case. If the NVF simulator is run on a cluster equipped with 1.5 GHz FT1500A CPUs,with 240 h and 256 processors for each case. However, only 72 h are taken for the cluster with 3.0 GHz Intel CPUs,leading to acceptable computational efficiency for the complex unsteady cases.

Fig.10 Static moment coefficients with different angles of attack of model and deflection angles of rudders.
As mentioned before, there are some physical limitations for the flight control device in actual situations. In this case,the maximum rudder deflection angle δ|Limitand the maximum rudder deflection velocity ωδ|Limitare limited in the range of±25° and 250 (°)/s, respectively. The initial values of control gain factors can be obtained through Flight Mechanics (FM)simulations. Generally, the fast-loop gain factor is set to be no more than 1/5 of that of the rudder deflection velocity,and the slow-loop gain factor is set to be about 1/5 of that of the fast loop,ensuring the time-scale separation.According to the flight mechanics simulation, we have obtained a group of initial control gain factors, kα=5 and kq=25 (Case1 in Table 2). For comparison, a case (Case 2 in Table 2) with larger gain factors (kα=10 and kq=50) is also considered. To eliminate the static error, two cases (Case 3 and Case 4 in Table 2) with the integrator are simulated. In addition, two other cases (Case 5 and Case 6 in Table 2) with different limitations are considered to test the influence of physical limitations, the limitations are discussed in next sub-sections.
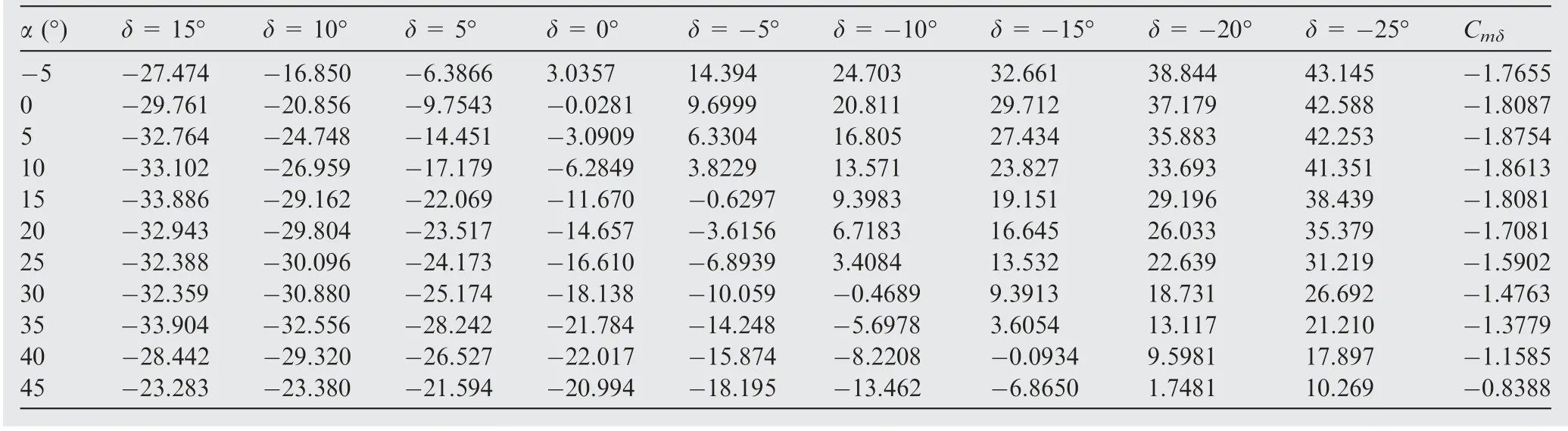
Table 1 Static moment coefficients and derivative with respect to deflecting angles.

Table 2 Six typical cases for different gain factors with and without integrator.
3.4. Pitching-up simulation without integrator
The NVF and FM results are compared in Case 1(Fig.11).In this figure, the left vertical axis displays the angular variables(the angle of attack of the model, and the deflection angle of the rudder), and the right vertical axis represents the angular velocity ω of the model. The legend ‘‘CFD” represents the NVF results, and ‘‘SIM” the FM simulation results by MATLAB-Simulink. Because the unsteady effects are fully taken into consideration in the NVF method, the unsteady aerodynamic forces will cause a delayed response, which cannot be captured by the FM simulation. Therefore, the CFDbased results show a lag behind those by the FM simulation.This phenomenon indicates the importance of using NVF to design control laws. In addition, there are some differences between the steady-state angles of attack of NVF and FM,though both the angles have a static error (about 1°) from the expected target angle due to the minor inaccuracy of the aerodynamic model.
The static error is briefly analyzed as follows. Substituting Eq. (7) into Eq. (11) at the ideal trimmed state, namely when the angle of attack is 30° and the pitching angular velocity is 0 (°)/s, the steady-state rudder deflection angle in the control law is


Since the static error ess>0, the rudder deflection angle increases with the control gain factors, resulting in the reduction of the static error. Thus, the two control gain factors are doubled for comparison (Case 2). The increments of the control gain factors can also accelerate the response, but too large gain factors may destabilize the whole system. For Case 2, the FM simulation results (the dash lines are shown in Fig. 12) have already tended to be divergent, but the NVF results (shown in Fig. 12) can still maintain convergence due to the unsteady effects. Namely, the damping becomes larger.However, to further reduce the static error or accelerate the response time,increasing the control gain factors may become invalid.
3.5. Maneuvering simulation with integrator
Inspired by Eq.(14),we add an integrator to the outer loop to further eliminate the static error.After adopting the integrator,we obtain the steady-state rudder deflection angle:

where Ihistroy= (αc-α)dt is the historical integral amplitude.When the ideal trimmed state is achieved(α-αc=0°),Ihistorybecomes constant and can completely eliminate the static error.
Two cases with the gain factors kiα=1 and 5 are simulated(Case 3 and Case 4 in Table 2). The results of these two cases are compared with those of Case 2,as shown in Fig.13.Introducing the integrator slightly reduces the response time of Case 3 and Case 4, but the overshoot is much deteriorated. The approaching rate to the steady-state value becomes slightly faster with increasing kiα(Fig.13(b)), but the overshoot is obviously greater. This phenomenon can be analyzed from the property of the integrator: when α <αc, Ihistoryis negative,leading to a larger rudder deflection, and finally resulting in a stronger pitching-up motion of the model.When α keeps growing and becomes larger than αc, Ihistoryremains negative in a certain range so that the missile will continue to enhance its pitching-up trend. The analysis is similar for the pitchingdown process: increasing the ‘inertia’ of the system relatively reduces the damping.Therefore,the response rate will become faster and the overshoot will also increase.

Fig.11 NVF and FM simulation results of Case 1.

Fig.12 NVF and FM simulation results of Case 2.

Fig.13 Comparison between Case 2, Case 3 and Case 4.
Due to the limited computing resources, the pitching process is simulated for only 2 s. However, at t=2 s, the results of the simulation with the integrator become even worse. It may take a long time (more than 10 s) to reach the expected value.A feasible way to reduce this time is to increase the gain factor kiα. However, this may cause the instability of the system. It follows that the part of IkqkiαIhistoryshould be limited.According to Eq. (15) and the expected trimmed angle of attack, IkqkiαIhistoryis 217.025. The limitation is thus set as |IkqkiαIhistory|<250 with kiαbeing 50 (Case 5 in Table 2).The numerical result is shown in Fig. 14. The overshoot is almost the same as that in Case 3 even though the integrating gain factor is increased by 50 times. The approaching rate to the steady-state value is increased slightly, so the performance of the controller is improved in a sense.

Fig.14 Comparison of results between Case 3 and Case 5.

Fig.15 Comparison of results between Case 1 and Case 6.
As shown in Fig. 15, the overshoot is not obviously weakened. According to the maximum angular velocity in Case 1,we introduce a restriction to the rudder angular velocity(Case 6 in Table 2)based on Case 5.The maximum angular velocity(ωmax)in Case 1 is 98.137(°)/s,so we choose the limitation of|qc|<120. The CFD-based NVF results are plotted in Fig. 15 and compared with those of Case 1.The overshoot almost disappears.Compared with the baseline in Case 1,the static error is eliminated and the response time is substantially shortened,which shows that the control performance is obviously improved.
We display the response performance in Table 3 for all the six cases. The steady-state angle of attack α∞, the steady-state rudder deflection angle δ∞,and the dynamic parameters(such as the rising time tr, the setting time tsand the overshoot σp)are compared. The rising time is defined as the response time when the model reaches the steady-state value for the first time; the setting time trrefers to the response time when the status of the model no longer exceeds a certain error band;the error band is defined as ±0.1°; the overshoot is the ratio between the exceeding response and the steady-state value. It is obvious that the static error is significantly reduced and that the rising time is greatly shortened with the increase of the control gain factors. However, if the rudder angular velocity qcis not limited, the setting time will increase because of the overshoot. By introducing the limitation of the rudder angular velocity (Case 6), the overshoot can be largely eliminated.
3.6.Comparison of flow structures of Case 1,Case 2 and Case 6
Since the pitching movements of Cases 2-5 are similar,we only compare the flow structures of Case 1, Case 2 and Case 6.Fig. 16 shows the model vortex by Q criteria (with various pressures colored) at six typical time points for Case 1, Case 2 and Case 6. The flow separation at the leading edge of both the forebody delta wings and the rudders can be seen at large angles of attack. However, at small angles of attack, the flow separation occurs only at the rudder tips (see the enlarged views in Fig. 17). For Case 2, because of the overshoot phenomenon, the maximum angle of attack is about 40°, causing much more serious flow separations.At t=0.5 s in Case 2,the flows over the fore-body delta wings and the rudders are fully separated (see the enlarged views in Fig. 17). At the final trimmed state(for example t=2.0 s),however,the flow structures of Case 1, Case 2 and Case 6 are almost the same with each other.
Fig.18 shows the spatial streamlines of the model of Case 6 at different time steps with different angles of attack during the pitching-up. The flow separation patterns with the angle of attack can be seen clearly. We will further validate the results with wind-tunnel experiments in the future.
4. Concluding remarks
A CFD/RBD/FCS coupled simulator is presented for multiphysics virtual flight simulations in this work. This simulator integrates the high-efficient parallel unsteady RANS solver,the dynamic hybrid grid generator, the 6-DOF flight mechanics solver, and the flight control law. An object-oriented integration framework can be developed for other multi-physics solver integration in the future. In order to handle maneuvering flights of vehicles with deflecting control surfaces,the overlapping grid technique is integrated into our dynamic grid generation package, and a parallel implicit hole-cutting method is developed to improve the efficiency of overlapping grid assembling. Both the loose and strong coupling CFD/RBD approaches are integrated into the simulator for different cases, while the flight control law is considered as an external input to activate the control surfaces. The nonlinear dynamic inversion method is adopted to design the flight control law of a maneuverable missile model in the pitching channel. Through the simulation and analysis of the maneuvering process, the baseline dynamic inversion control law is improved, and a set of better control gain factors is obtained.
The test cases show that,for the rapid maneuvering of aero vehicles at large angles of attack, flight mechanic simulations may often result in large errors due to the inaccurate approximation of the aerodynamic model.The CFD-based NVF simulation is able to provide more reliable closed-loop response characteristics of the control system because it has taken into account the strong unsteady effects of the controlled plant.More importantly, based on this study, we can realize integrated multi-disciplinary optimization by using the NVF tools in the future.

Table 3 Comparison of response parameters of six cases.

Fig.16 Vortex calculated by Q criteria (colored by local pressure coefficient) for different cases (Left: Case 1, Middle: Case 2, Right:Case 6).

Fig.17 Enlarged views of vortex calculated by Q criteria(colored by local pressure coefficient)near the rudders for different cases(Left:Case 1, Middle: Case 2, Right: Case 6).

Fig.18 Spatial streamlines for Case 6 at different time points.
Acknowledgements
This work is supported partially by National Key Research and Development Program (No. 2016YFB0200701) and National Natural Science Foundation of China (Nos.11532016 and 11672324).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Numerical investigation of flow mechanisms of tandem impeller inside a centrifugal compressor
- Experimental investigation on dynamic response of flat blades with underplatform dampers
- Non-random vibration analysis for general viscous damping systems
- Numerical analysis of hypersonic thermochemical non-equilibrium environment for an entry configuration in ionized flow
- Prediction of nonlinear pilot-induced oscillation using an intelligent human pilot model
- Multiple hierarchy risk assessment with hybrid model for safety enhancing of unmanned subscale BWB demonstrator flight test
