Experimental investigation on dynamic response of flat blades with underplatform dampers
2020-01-09DyiZHANGBinGAOJieHONGJinweiFUXingyunGE
Dyi ZHANG, Bin GAO, Jie HONG,c,*, Jinwei FU, Xingyun GE
a School of Energy and Power Engineering, Beihang University, Beijing 100083, China
b Beijing Key Laboratory of Aero-Engine Structure and Strength, Beijing 100083, China
c Collaborative Innovation Center of Advanced Aero-Engine, Beihang University, Beijing 100083, China
Abstract One test rig with three blades and two Under-Platform Dampers (UPDs) is established to better understand the dynamical behavior of blades with UPDs. A pre-loaded spring is used to simulate the centrifugal load acting on the damper,thereby achieving continuous adjustment of the pressing load.UPDs with different forms,sizes and materials are carefully designed as experimental control groups.Noncontact measurement via a laser Doppler velocimeter is employed and contact excitation which is performed by an electromagnetic exciter is adopted to directly obtain the magnitude of the excitation load by a force sensor mounted on the excitation rod.Particular attention is paid to the influence of the contact status of the contact surfaces,e.g.the pressure-sensitive paper is used to measure the effective contact area of the UPDs. The experimental variables are selected as the centrifugal force, the amplitude of the excitation force, the damper mass, the effective contact area,and the damper material.The Frequency Response Function(FRF)of the blade under different experimental parameters is obtained by slow frequency sweep under sinusoidal excitation to study the influence of each parameter on the dynamic characteristics of the blade and the mechanism analysis is carried out combined with the experimental results.
KEYWORDS Effective contact area;Forced response;Friction;Test rig;Turbo machinery;Underplatform dampers
1. Introduction
The suppression of blade vibration is an important issue in the design of aero-engines.In order to mitigate the harmful vibration,dry-friction damping,as an efficient damping technology,is now widely used in the vibration reduction of the blade,including various structural forms such as shroud, underplatform damper, dovetail-groove, etc.,1-8among which the Under-Platform Damper(UPD)is widely used in fans and turbine blades because it does not affect the airfoil nor airflow passages,and its additional centrifugal load is relatively slight.
Many scholars are committed to the study of the dynamic characteristics of the blade with UPDs. Petrov9developed a method for calculating directly resonance frequency and resonance amplitude of the nonlinear vibration of bladed disks based on multiple harmonic balance method; Zhang et al.10developed a numerical method for calculating the steadystate vibration response of blades with multi scattered friction contacts; Panning et al.11analyzed the influence of damper mass and contact geometry on the energy dissipation based on numerical results, which provides a basis for the optimization of UPD.In order to further study the damper-blade interaction and verify the accuracy of the proposed numerical method, many experimental researches are also carried out at the same time. The most common experimental setup is a structure in which a single damper is placed between two blades and pulled by dead weight through wires simulating the centrifugal force.12-16Sanliturk et al.17measured the dynamic response of the test rig comprising two blades as well as one damper and compared it with the numerical results.The research shows that UPDs are prone to rolling motion, which reduces the damping effect usually in the lower nodal diameter bladed-disk modes. Bessone et al.18studied the effects of different damper centrifugal pressing forces on the damping effect by using a test rig consisting of two turbine blades of huge dimensions that are normally in service and an asymmetric UPD. His work highlighted the contribution to the system damping due to the friction at the root of the blade compared to the damping introduced by the UPD. A more complex experimental device consists of an integral bladed disk fitted with UPDs. Berruti et al.19used a static bladed disk excited with noncontact traveling wave generated by electromagnets placed under each blade to study the damper behavior at different nodal diameters of the disk. Dampers were loaded with dead weights as well. Sever et al.20designed a rotating test rig to simulate the centrifugal load of the blade and the damper in a more realistic way. The excitation force was simulated by employing a permanent magnet fixed to the rig. In this case,however,experimental results can be affected by possible presence of mistuning.21,22In recent years, some scholars have been working on damper kinematics and micromechanics,for a better understanding of the dynamics of the damper in depth.23,24In their experiments, forces exchanged between the platform and damper contact surfaces and the kinematics in terms of damper/platform relative displacement were measured. Namely for each point on Frequency Response Function (FRF), the corresponding hysteresis at the contacts,force equilibrium and platform kinematics can be reconstructed. Gola et al.25found that the damper exhibited a variety of different behavior under the same input condition, and the damper-platform system always converges to the solution with the lowest hysteresis area.
The experimental researches that have been carried out can still be further improved in the following aspects:
(1) The common experimental setup is one damper placed between two blades.However,the vibration characteristics of a single blade in actual operating condition are obviously affected by two dampers. Therefore, it can be interesting to build a test rig consisting of three blades and two dampers,which is more consistent with the real conditions intuitively, and then we can focus on the dynamic characteristics of the middle blade in the test.Simultaneously, this approach avoids the cumbersome tuning process when using a rotating test rig with integral bladed disk due to possible presence of mistuning.
(2) In aero-engine applications,the UPD is very small.One UPD weights from 0.8 g to 1.5 g in some cases, and therefore the contact status between the damper and the platform is always complicated due to the flexibility of UPD, machining errors, rotation speed, operation temperature, etc. The influence of the contact status of contact surfaces is considered insufficiently in related experimental researches.However,the vibration characteristics of the blade is directly influenced by the change of contact status.Therefore,it is significative to pay particular attention to the test of the contact status (typically such as the effective contact area).
(3) There is still a need for systematic and comprehensive research on the influence of key damper structural parameters on blade dynamic characteristics from the perspective of damper design. In this paper (in Section 3.1 below),the parameters of the blade-damper system are divided into three categories: damper structural design parameters,contact surface parameters and blade dynamic parameters. While focusing on the structure design of the UPDs,the experiment is arranged to reveal the interaction between these three types of parameters and to obtain principles of structural optimization of the UPDs in engineering practice.
2. Test rig for blades with UDPs
The overall scheme of the test rig for the blades with UPDs is shown in Fig. 1. The experimental device mainly consists of blades and their installation base,UPDs and their loading system, excitation system and measurement system. During the experiment, the middle blade is excited by an electromagnetic exciter and the vibration response of the blade is obtained using Polytec laser Doppler vibrometer. The effective contact area of the contact surfaces between platforms and UPDs is measured by the pressure-sensitive paper. The main components of the test rig are shown in Fig. 2.

Fig.1 Overall schematic diagram of test rig.

Fig.2 Main components of test rig.
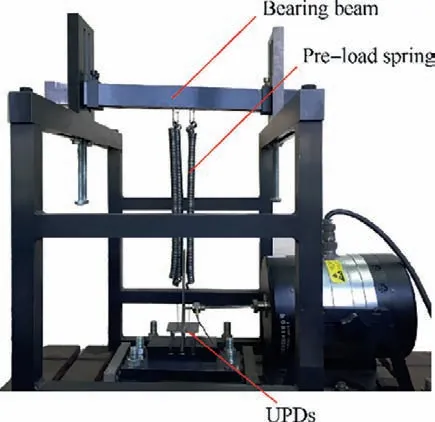
Fig.4 Loading assembly of UPDs.
2.1. Blade specimen and installation
The test rig adopts a structural scheme including three blades and two dampers. Dampers are installed on both sides of the middle blade,which is required to be directly excited and measured during the test.To facilitate the excitation and measurement of the middle blade,only the dovetail and platform parts of the blades on both ends are retained,as shown in Fig.3(a).The dimensions of the flat blade are given in Fig.3(b).In order to simulate the centrifugal load of the blades in rotating condition, threaded holes are opened under the groove of the blade installation base,through which each pair of the dovetail and the groove is tightened by two bolts, providing a maximum pressing force of 30000 N.
2.2. Loading assembly and damper specimen
2.2.1. Loading assembly of centrifugal load
In order to achieve continuous adjustment of the damper pressing force, and avoid the effects of additional friction between the pulley block and the ropes when the damper is pulled by dead weight,in this experiment the pre-loaded spring is used to simulate the centrifugal load that the damper is subjected to.The lower end of the spring is connected to the damper through a wire,and the upper end is connected to a heightadjustable bearing beam.The pressing force of the damper can be continuously adjusted by changing the height of the bearing beam to adjust the spring elongation, as shown in Fig. 4.

Fig.3 Blade specimen and installation.
2.2.2. Damper specimens
The typical structures of UPDs can be divided into the sheet type, the prismatic type, the spring type and the box type,17,26-30as shown in Fig. 5.31The UPD of the sheet type is lighter in weight, generally around 1.0 g, which means few additional centrifugal load of the damper, yet less friction and pressing force. Moreover, additional mounting structure for damper installation is required under adjacent platforms of the blades. The UPD of the prismatic type can be designed for a larger mass, consequently providing greater dry friction damping and pressing force. In addition, both the upper surface and the side surface of the damper can generate frictional energy dissipation.This kind of UPD is commonly used for the vibration reduction of the blade of large size in ground-based gas turbines.The UPDs of the spring type and the box type are of moderate mass and fitted by pre-compression selfdeformation. In the structure design, it is necessary to ensure a satisfactory contact status at the rotation speed for the last two kinds to keep the damping effect stable.

Fig.5 Typical UPDs in aero-engine.31

Fig.6 Damper dimensions (front view).
This experimental research only focuses on the UPD of the sheet type.The vibration characteristics of sheet dampers with different structural forms or materials are tested. The length and width of each tested damper,the position and diameter of the openings are the same,as shown in Fig.6.The serial number of the damper and its cross section parameter are given in Table 1.
2.3. Excitation system
There are two ways for exciting the blade: contact and noncontact. The advantage of non-contact excitation is that the excitation system is physically isolated from the blade, avoiding the mechanic influence (additional mass, stiffness and damping) of the excitation system on the vibration characteristics of the blade. However, the magnitude of the exciting force cannot be directly measured by the way of non-contact excitation.In this study,contact excitation which is performed by an electromagnetic exciter is adopted to directly obtain the magnitude of the excitation load by the force sensor mounted on the excitation rod.
The interaction between the excitation rod and the excited blade during the experiment would affect the inherent characteristics of the blade through exerting additional stiffness anddamping effects on the blade.In order to reduce this effect,the excitation position of the excitation rod is selected in the vicinity of the nodal line near the blade root during the experiment.In addition,in order to reduce the vibration coupling between the excitation system and the blade, and ensure that the electromagnetic exciter provides a stable sinusoidal excitation force in the low frequency range, the vibration exciter is independently mounted on the test bench, as shown in Fig. 7.

Table 1 Serial number and parameters of damper.

Fig.7 Overall layout of test rig.
2.4. Measurement system
2.4.1. Measurement of effective contact area
In the research on damping mechanism and numerical analysis of the UPD, it is generally considered that the friction surface between the damper and the platform is in complete contact.17,32,33However, in actual applications, the effective contact area between the damper and the platform is limited due to structure deformation caused by centrifugal force and machining errors. It is more necessary to pay attention to the effective contact area for the damper with a cambered contact surface. In order to measure the effective contact area, a pressure sensitive paper is placed between the damper and the platform, and the effective contact area of the two is obtained according to the color distribution of the paper under different pressing forces. The area in the pressure sensitive paper would turn red where the pressure exceeds the threshold of the paper.
Fujifilm prescal ultra-low pressure test paper and low pressure test paper are selected in the experiment. The threshold values of these two types of pressure sensitive papers are 0.5 MPa and 10 MPa respectively, of which the error does not exceed ±10%.
2.4.2. Measurement of vibration response
The Polytec full-field scanning laser test system is used to measure the vibration velocity and displacement of the key points of the blade.One focused aspect is the influence of the damper on the first-order natural frequency and resonant response of the blade, considering the additional stiffness and damping effects on the blade from the UPD.
3. Experimental method
3.1. Experimental variables
The parameters of the blade-damper system can be classified as damper structural design parameters, contact surface parameters and blade dynamic parameters, as shown in Fig. 8. The damper structural design parameters are directly oriented to the engineering design of the damper; the contact surface parameters comprehensively describe the contact status and mechanical properties of the contact surface on a mesoscopic scale; the blade dynamic parameters are physical quantities that describe the inherent characteristics of the blade vibration and the damping effect of the damper on a macro scale. The damper structural design parameters and engine working conditions (temperature, rotating speed, aerodynamic excitation,etc.) together determine the contact surface parameters. The contact surface parameters directly determine the contact friction,which can directly cause changes in the vibration characteristics of the blade, namely the blade dynamic parameters.
This research focuses on the influence of the damper structural design parameters and contact surface parameters on the blade dynamic parameters.The vibration response of the blade under different experimental parameters is measured, and the mechanism analysis is carried out combined with the experimental results.

Fig.8 Relationship among damper structural design parameters, contact surface parameters and blade dynamic parameters.
The structural and geometric parameters of the damper determine its mass and stiffness distribution. Under the centrifugal load, the damper is elastically deformed and pressed under the platform. The centrifugal force of the damper is determined by the combination of mass and rotating speed.The contact form between the UPD and the platform is surface-to-surface contact, which has a large contact area.The contact pressure distribution and effective contact area are mainly affected by external load and contact surface geometry. Under aerodynamic excitation, the damper and the platform move relative to each other. The relative displacement between the contact surfaces is mainly determined by the mass of the damper,the centrifugal force,the amplitude of the excitation force and the friction coefficient. At the same time, the damper mass, the friction coefficient and the contact stiffness are all affected by the damper material.
It can be seen that the damper structure design parameters and the contact surface parameters have coupling effects on the blade dynamic parameters. Thus, the variable-controlling approach is adopted to study the influence of single parameter on the dynamic characteristics of the blade,and the experimental variables are selected as the centrifugal force,the amplitude of the excitation force, the damper mass, the effective contact area, and the damper material.
3.2. Experimental procedure
In the experiment,the FRF of the blade in a certain frequency range is obtained by slow frequency sweep under the sinusoidal excitation. During the sweeping process, the input voltage of the electromagnetic exciter is kept constant. Due to the characteristics of the exciter,the magnitude of the output excitation force changes with the excitation frequency. Thus, the blade vibration response measured is not under constant excitation force because of the limitations of the equipment. In order to obtain the FRF, firstly, the response amplitude of the blade is divided by the amplitude of the excitation force at the same frequency,obtaining the response amplitude under unit force at this frequency, and then, the points of the response amplitude under unit force at different frequencies are connected to obtain the FRF curve. The FRF curve of 5#UPDs with cambered contact surfaces under a spring preload of 20 N is shown in Fig. 9. Since the spring preload and the effective contact area between the damper and the platform is quite small, neither the additional stiffness nor the damping caused by the damper contributes much,the system is close to one linear system without UPD.
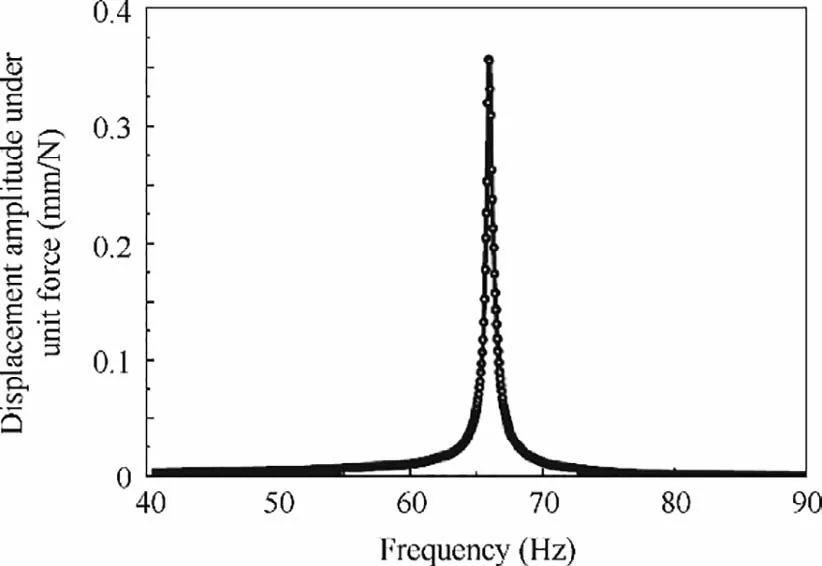
Fig.9 FRF curve of blade with 5#UPD under a spring preload of 20 N.
The vibration amplitude at each frequency obtained by the frequency sweep deviates from the amplitude of the steadystate vibration of the blade. If the sweep rate is too fast, the wrong FRF may be obtained.Fig.10 shows the velocity amplitude curves of the blade vibration at different sweep rates for a certain experimental parameter. It can be found that the obtained velocity amplitude curves are basically coincident with a sweep rate lower than 2.5 Hz/s.Therefore,the vibration amplitude at each frequency obtained by the frequency sweep can be regarded as the amplitude of the steady-state vibration of the blade when the sweep rate is lower than 2.5 Hz/s. Since only the vibration near the first-order bending frequency of the blade is concerned, the sweep frequency selected in this experiment ranges from 45 Hz to 90 Hz, the total sweep time is 100 s, and the sweep rate is 0.45 Hz/s.
4. Results and discussion
4.1. Influence of centrifugal force
The FRF curves of the blade with 2#UPD under different centrifugal forces (Fc) obtained by the experiment are shown in Fig. 11.
It can be seen that the UPD has additional stiffness and damping effect on the blade. The first-order resonant frequency and resonant response of the blade are changed under different centrifugal forces, as shown in Fig. 12.

Fig.10 FRF curves at different sweep rates.

Fig.11 FRF curves of blade with 2#UPD under different centrifugal forces.

Fig.12 First-order resonance characteristics of blade with 2#UPDs under different centrifugal loads.
As the centrifugal force of the damper increases, the firstorder resonant frequency of the blade rises and tends to be constant. When the centrifugal force reaches 340 N, the firstorder resonant frequency increases by 10%. Therefore, the influence of the UPD on the blade resonance margin must be considered in engineering design. The first-order resonant frequency of the blade increases as the centrifugal force increases, for the increased force causes larger additional stiffness generated by the damper. When the centrifugal force exceeds a certain threshold, the contact surface enters a fully stuck state, and simultaneously the additional stiffness of the damper reaches a maximum value, so the first-order resonant frequency of the blade tends to be a constant value.
As the centrifugal force of the damper increases, the resonant response of the blade decreases first and then increases.There exists an optimal value of centrifugal force that has the biggest effect on suppressing the vibration of the blade.It can be defined that the centrifugal force that minimizes the resonant response of the blade is the optimal centrifugal force in this condition (the optimal centrifugal force under the experimental parameter in Fig. 12 is about 100 N). When the centrifugal force of the damper is relatively small,the blade and the platform are mainly in the slip contact status.The friction force increases as the centrifugal force increases,and thus the dissipating effect of the damper increases so that the resonant response of the blade decreases. When the centrifugal force of the damper grows greater than the optimal centrifugal force, as the centrifugal force increases, the contact status gradually changes to a mainly stuck state, and the energy dissipation of the damper decreases so that the damping effect becomes worse.
The experimental results show that for the blade with other UPDs tested, the vibration response characteristics of the blade are similar to the above results when the centrifugal force changes.
4.2. Influence of amplitude of excitation force
Under different amplitudes of the excitation force,the changes of the first-order resonant frequency and resonance response of the blade with the centrifugal force obtained by the experiment are shown in Fig.13,where the amplitudes of the excitation force (Fe) are sorted as Fe5>Fe4>Fe3>Fe2>Fe1.

Fig.13 First-order resonance characteristics of blade with 2#UPDs under different amplitudes of excitation force.
It can be seen from Fig.13(a)that under the same centrifugal force, the smaller the amplitude of the excitation force is,the higher the first-order resonant frequency of the blade is,which is more prominent in the case of a small centrifugal force. Since the vibration amplitude of the platform decreases as the amplitude of the excitation force decreases, the proportion of the slip contact status in one period of vibration decreases. Thus, the equivalent stiffness34of the friction increases so that the first-order resonant frequency of the blade increases.
It can be seen from Fig. 13(b)that as the magnitude of the excitation force increases, the damper can provide excellent damping effect over a wider range of centrifugal forces, that is,only under large vibration amplitudes can the damper work effectively. It also means that if the stiffness of the blade root extending section is too strong, or the cascade solidity is too high,the vibration amplitude of the platform could be so small that the damper is difficult to exert its effect. This is because when the vibration amplitude of the platform is large,the contact status between the blade and the platform is maintained as mainly slip state in one period of vibration over a wide range of centrifugal forces so that the damper can achieve an excellent damping effect.
The experimental results show that for the blade with other UPDs tested, the vibration response characteristics of the blade are similar to the above results when the amplitude of the excitation force changes.
During the experiment, the magnitude of the excitation force changes with the excitation frequency due to the limitation of the electromagnetic exciting system. The magnitude of the excitation force becomes smaller near resonant frequencies compared to that far from resonance.On the one hand,under the conditions of quite small spring preload, the damper’s effects of additional stiffness and damping on the blade are not significant. The system under this circumstance is close to one linear system without UPD. When it comes to the conditions of fairly large spring preload, the contact status between the blade and the platform is maintained as stuck state during vibration. Thus, the UPDs act as an elastic connection between adjacent blades and the system turns to be close to a linear system again. Therefore, the non-constant excitation force has little impact on the upper and lower limits of the system resonant frequency in Fig. 13(a). On the other hand,as the magnitude of the excitation force becomes smaller near resonant frequencies compared to the cases of constant excitation force, from Fig. 13(b), when a large spring preload is applied, the resonant amplitude under unit force obtained from the experiment would be larger than that of constant excitation force. Thus, the non-constant excitation force leads to a conservative evaluation on the damping effect of UPD.When it comes to the condition of a relatively slight spring preload,the conclusion,however,is opposite.Therefore,the nonconstant excitation force causes the deviation in the evaluation of the damping effect during tests.
4.3. Influence of damper mass
The 3# and 4# dampers have different mass, which are both made of aluminum, identical in the size of contact surface and different only in thickness. Fitted with dampers of different mass,the changes of the first-order resonant frequency and resonance response of the blade with the centrifugal force obtained by the experiments are shown in Fig. 14.
Fig. 14(a) and (b) indicate that under the same centrifugal force and amplitude of the excitation force,the first-order frequency of the blade increases as the mass of the damper decreases. This is because the smaller the mass of the damper is, the easier it is for the damper to move with the platform,and thus the proportion of the stuck contact status over one cycle of motion increases, so that the equivalent stiffness of the friction increases and the resonant frequency of the blade increases.
Fig.14(c)and(d)indicates that when the mass of the damper is increased, the range of the optimum centrifugal force is broadened. The centrifugal force of the damper is determined by its mass and the rotating speed, among which the rotating speed of the aero-engine is generally determined. In actual practice,we prefer to adjust the damper mass to make the centrifugal force in operating state as close as possible to the optimal centrifugal force, but this is hard to realize. In this case,the mass of the damper can be increased appropriately to ensure that the damper has a considerable damping effect over a wider range of centrifugal force.
The experimental results show that for the 1#and 2#dampers, the vibration response characteristics of the blade with dampers of different mass are similar to the above.
4.4. Influence of effective contact area

Fig.14 First-order resonance characteristics of blade with dampers of different mass.

Fig.15 Contact pressure distribution of dampers with different configurations.

Fig.16 First-order resonance characteristics of blade with dampers of different effective contact areas.

Fig.17 Relationship between friction and displacement from microslip model with different effective contact areas.35
The contact pressure distribution of the 1#, 5#, and 6# dampers measured by the pressure sensitive paper at the centrifugal force of 200 N is shown in Fig.15.When the contact surface of the damper is flat(as 1#damper),the contact surface between the platform and the damper fits well, so the contact pressure distribution is uniform and there is no obvious contact pressure concentration area, and thus the effective contact area between the damper and platform is large,as shown in Fig.15(a).When the contact surface of the damper is cambered(as 5#and 6# dampers), only the middle portion of the damper is in contact with the edge of the platform, so the contact area is small and a significant contact pressure concentration area is generated on the contact surface, as shown in Fig. 15(b). The face-to-face contact gradually degenerates into a line-to-line contact as the curvature of the cambered surface increases,as shown in Fig. 15(c).
Under three different effective contact areas,the changes of the first-order resonant frequency and resonance response of the blade with the centrifugal force obtained by the experiment are shown in Fig. 16.
From Fig.16(a),it is found that the first-order resonant frequency of the 1#damper with a larger effective contact area is higher than the 5# and 6# dampers with a smaller effective contact area. Fig. 17(a) shows the friction-displacement (f-x)curve with different effective contact areas but the same centrifugal pressing force according to Iwan’s parallel-series model.35The larger the effective contact area of the damper is, the greater the tangential contact stiffness of the contact surface is, and thus the resonant frequency of the blade increases.
From Fig. 16(b), it is found that the resonance response gets greater with smaller effective contact area under the same centrifugal force.Considering a small effective contact area,on the one hand, it is not conducive to the energy dissipation through distributed friction damping; on the other hand, for the contact pressure concentration area, the proportion of the stuck contact status in one period of vibration increases,so the equivalent damping36of the friction decreases. Fig. 17(b) shows the hysteresis loops with different effective contact areas but the same centrifugal pressing force according to Iwan’s parallel-series model.35It is obvious that the hysteresis loop area is significantly reduced with less effective contact area when the relative displacement amplitude between the damper and the platform is the same. Therefore, in practical engineering, the effective contact area of the damper is required to be as large as possible to improve the damping effect.
4.5. Influence of damper material
The 2#and 4#dampers are identical in geometry but different in material. Fitted with dampers of different materials, the changes of the first-order resonant frequency and resonance response of the blade with the centrifugal force obtained by the experiment are shown in Fig. 18.
The material mainly affects the mass of the damper and the friction coefficient of the contact surface. The density of aluminum is about 1/3 of the density of steel, so the mass of the aluminum damper is about 1/3 of the mass of the steel damper.The friction coefficient between the aluminum damper and the platform is about 0.3,while that between the steel damper and the platform is about 0.2.

Fig.18 First-order resonance characteristics of blade with dampers of different materials.
Under the same conditions, the smaller the mass of the damper is, the easier it is to move with the platform, the greater the equivalent stiffness of the friction force is;the larger the friction coefficient of the contact surface is, the greater the equivalent stiffness of the friction force is. It can be seen from Fig. 18(a) that under the combined effect of the damper mass and the friction coefficient, the resonant frequency of the blade with the aluminum damper is larger,which is more obvious in the range of small centrifugal force.
Under the same conditions, a smaller damper mass is not conducive to the relative movement between the damper and the platform,nor the friction energy dissipation;a greater friction coefficient of the contact surface has benefits to the friction damping in the microslip region. It can be seen from Fig. 18(b) that under the condition of small centrifugal force,the resonant response of the blade with the steel damper is smaller, and at this time the relative displacement between the steel damper which has a larger mass and the platform is larger;under the condition of large centrifugal force,the resonant response of the blade with the aluminum damper is smaller, and at this time the friction energy dissipation in the microslip region of the aluminum damper which has a larger friction coefficient is larger.
From the above analysis, it is found that when multiple parameters of the damper change simultaneously,the damping effect of the damper is difficult to quantitatively evaluate under the combined effect of multiple parameters. Therefore, it is necessary to develop a numerical simulation method to predict the nonlinear dynamic response of blades with multi scattered dry friction contacts, which is of great significance for the design and optimization of the UPD.
4.6. Comparison of experimental results and numerical simulation results
The numerical simulation method developed in Ref.10is used here to calculate the response. By giving different amplitudes of the excitation force, the first-order resonant frequency and resonance response of the blade with 2# damper are obtained as Fig. 19, and the experimental results are shown in Fig. 13,where the amplitudes of the excitation force (Fe) are sorted as Fe5>Fe4>Fe3>Fe2>Fe1.

Fig.19 First-order resonance characteristics of blade with 2#UPDs under different amplitudes of excitation force, obtained by numerical simulation.
The numerical results are basically coherent with the experiment. As the amplitude of the excitation force increases, the first-order resonant frequency of the blade under the same centrifugal force decreases, while the optimal centrifugal force of the damper increases. The difference between the simulation and the experiment result is mainly caused by the simplified contact model adopted in calculation. The damper is modelled as a spring in series with a Coulomb friction and the contact stiffness along both perpendicular and tangential directions are set as constants in such a large range of spring preload tested in the experiments. The contact stiffness during calculation is adjusted to be a relatively large value, in order to match the resonant frequency of the experimental results under large centrifugal forces.Therefore, when the centrifugal force decreases, the contact status between the platform and the UPD would undergo a rapid shift from sticking to slipping in the simulation, which leads to the sudden drops of the curves in Fig. 19. But in reality, as the spring preload and the contact status change greatly, the contact stiffness between the platform and the UPD changes along with them, which is not considered in the simulation. A more complex and realistic friction model is required to improve the simulation accuracy.
5. Conclusions
The test rig with three blades and two UPDs established in this paper is convenient and effective to test the dynamic characteristics of the blades-dampers system. The experimental method adopted is valid in controlling the variables to obtain the influence of each key design parameter of the UPD on the system response.
The results show that the first-order resonant frequency of the blade increases with the increase of centrifugal force acting on the UPD, and the increasement can reach 10%; an optimal value of centrifugal force exists, which has the biggest effect on suppressing the vibration of the blade; the range of optimal centrifugal force is broadened by the increase of the mass of UPD; a larger amplitude of the platform vibration brings a wider range of the centrifugal force under which the UPD can effectively suppress the vibration;UPDs made of a material with a bigger coefficient of friction promote the energy dissipation of micro-slip region on the contact surfaces under the condition of large centrifugal force; the robustness of the damping effect of the UPD can be improved by increasing the uniformity of the contact pressure on the contact surfaces.
This paper focuses on the influence rules obtained by experiments, and the following investigation will concentrate on how to introduce one more precise friction model to improve the simulation accuracy and the solution efficiency as well.
Acknowledgement
The authors would like to thank for the financial support from the National Natural Science Foundation of China (Nos.11772022, 91860205 and 51475021), and the experimental devices provided by Key Laboratory of Vibration and Control of Aero-Propulsion System,Ministry of Education,Northeastern University (VCAME201602). Special thanks to ZHANG Qicheng and DOU Yifei for their helpful advices on the paper writing.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- A CFD-based numerical virtual flight simulator and its application in control law design of a maneuverable missile model
- Numerical investigation of flow mechanisms of tandem impeller inside a centrifugal compressor
- Non-random vibration analysis for general viscous damping systems
- Numerical analysis of hypersonic thermochemical non-equilibrium environment for an entry configuration in ionized flow
- Prediction of nonlinear pilot-induced oscillation using an intelligent human pilot model
- Multiple hierarchy risk assessment with hybrid model for safety enhancing of unmanned subscale BWB demonstrator flight test
