Numerical analysis of hypersonic thermochemical non-equilibrium environment for an entry configuration in ionized flow

Jianlong YANG, Meng LIU

School of Aeronautical Science and Engineering, Beihang University, Beijing 100083, China

KEYWORDS Catalysis;Heat flux;Hypersonic;Ionization;Thermochemical

Abstract A theoretical methodology for thermochemical non-equilibrium flow combing with the HLLC(Harten-Lax-van Leer Contact)scheme was applied to study the hypersonic thermochemical non-equilibrium environment of an entry configuration in ionized flow.A two-temperature controlling model was utilized and the Gupta’s 11 species(N2,O2,NO,O,N,NO+,N2+,O2+,N+,O+,e-)thermochemical non-equilibrium model was taken. Firstly, numerical calculations of hypersonic thermochemical non-equilibrium environments for different aerodynamic shapes were carried out to verify the reliability of the method above. Then, the method was used to research the effects of ionization and wall catalysis on the hypersonic thermochemical non-equilibrium environment of the entry configuration in ionized flow.The shock stand-off distance can be reduced by thermochemical reactions but doesn’t continue to decrease significantly when ionization occurs.The shock stand-off distance calculated by the 11 species model is 4.2% smaller than that calculated by the 5 species(N2,O2,NO,O,N)thermochemical non-equilibrium model without considering ionization.Ionization reduces wall heat flux but increases wall pressure a little. The effect of ionization on aerothermal loads is greater than that of aerodynamic loads.The thermochemical reactions of electrons and ions catalyzed at the wall increase wall heat flux significantly but make a small change in wall pressure.The maximum wall heat flux obtained by only considering the electrons and ions catalyzed at the partially catalytic wall condition is 11.8% less than that calculated at the supercatalytic wall condition.

1. Introduction

The flow temperatures after strong shockwaves increase rapidly when vehicles fly at hypersonic speeds.The hypersonic thermochemical non-equilibrium phenomena such as vibration, dissociation and ionization occur in high flow temperatures.1,2With the increase of hypersonic aerodynamic heating effect, the ionized species around the hypersonic vehicle will generate a plasma layer and cause the blackout with communication difficulty.3What’s worse, the structures seriously damaged by the extreme thermal loads may cause the flight mission to fail. Therefore, it’s necessary to effectively predict the hypersonic aerodynamic heating environments for the optimal design of Thermal Protection System (TPS)4,5and the flight safety of a hypersonic vehicle.

Lots of researches have been done to effectively predict the hypersonic aerodynamic heating environments of vehicles in thermochemical non-equilibrium air flows. Wang et al.6compared the performances of Dunn & Kang7, Gupta8, Park(1988)9and Park (1991)10chemical kinetic models in hypersonic aerodynamic heating environments calculations. They considered that the difference in wall heat fluxes was mainly caused by the chemical reaction rates of different kinetic models. Tchuen and Zeitoun11researched the method of computing the backward reaction rate by using different equilibrium constants. They found that the flow field structure, shockwave shape and surface properties were seriously affected by the equilibrium constants chosen. The equilibrium constants obtained from the fitting of experimental data were more reliable than those calculated by the theoretical formulations. Clarey and Greendyke12utilized the Park’s two-temperature model13and the three-temperature model to analyze the thermochemical non-equilibrium flows around a reentry vehicle. They found that the differences in the maximum number densities of electrons, temperature modes and species concentrations along the stagnation streamline calculated by the two-temperature and three-temperature models were very small. Edwards14presented an implicit multi-grid algorithm for computing hypersonic viscous flows with thermal and chemical non-equilibrium. He obtained the distributions of temperature and pressure along the stagnation streamline by using the 11 species chemical reaction model.Prakash et al.15developed a fifth-order shock-fitting numerical method to simulate the hypersonic thermochemical nonequilibrium flows over blunt bodies. The new method was capable of capturing the hypersonic flow field with highorder accuracy but without any oscillations near the shockwave. In addition, Farbar et al.16studied the effect of electron thermal non-equilibrium on hypersonic flow fields;Zeng et al.17proposed a new method to express the vibrational thermal conduction in numerical calculations of hypersonic thermochemical non-equilibrium flows.

In this study, a theoretical methodology for thermochemical non-equilibrium flow combing with the HLLC scheme18is applied to study the hypersonic thermochemical nonequilibrium environment of an entry configuration in ionized flow. The high temperature flow after shockwave is treated as a mixture of 11 species (N2, O2, NO, O, N, NO+,N2+, O2+, N+, O+, e-). A two-temperature controlling model is utilized and the Gupta’s thermochemical nonequilibrium model8is used. In order to effectively verify the reliability of the method above, the method is taken to calculate the hypersonic aerodynamic heating environments of two different aerodynamic shapes in advance.The method is then applied to research the effects of ionization and wall catalysis on the hypersonic thermochemical non-equilibrium environment of the entry configuration in ionized flow.

2. Governing equations and numerical method

2.1. Governing equations for hypersonic thermochemical nonequilibrium flow

The hypersonic ionized flow with thermal and chemical nonequilibrium described by the two-temperature model13,19is governed by the compressible Navier-Stokes equations. The conservation equations of mixture mass,species mass,mixture momentum, total energy and total vibrational-electronic energy are given as follows20:

where δij=1 if i=j,and δij=0 if i ≠j.t is time,ρ is the mixture density,xiis the ith axial direction,uiand ujare the velocity components along i and j directions:Ys，Ds， ˙ωsand hsrefer to the mass fraction,diffusion coefficient,mass formation rate and specific enthalpy of species, respectively; P is the mixture pressure, τijis the component of viscous stress tensor, e is the specific mixture internal energy, and h is the specific mixture enthalpy; qtr，iand qve，iare the translational-rotational and vibrational-electronic heat flux components along i direction;Nsis the total number of species,and Nmis the number of molecule species; ωvedenotes the mixture vibrationalelectronic energy source term, eveis the specific mixture vibrational-electronic energy, and eve，sis the specific vibrational-electronic energy of species.

2.2. Numerical method for hypersonic calculation

The HLLC flux-splitting scheme is a prominent Riemann solver.It’s quite robust and efficient for numerical calculations21.The numerical interface flux Ffof HLLC scheme is expressed as follows21,22:

where p*is the average pressure between two acoustic waves,and c is the speed of sound. SMis the contact wave velocity,SLand SRare the smallest and largest velocities of acoustic waves, respectively. ～ϑ and ～c are the Roe’s average variables of directed velocity and speed of sound.

The finite volume method is utilized for hypersonic aerodynamic heating environment numerical calculations. The inviscid fluxes are calculated by the HLLC scheme while the viscous fluxes are solved by the central difference scheme. In order to prevent the oscillations caused by the large flow gradients,the minmod limiter23is taken to reduce the slopes used in the interpolation of flow variables to the cell faces.The convergence of hypersonic numerical calculations is achieved when the variation of total energy doesn’t change more than 1%.

3. Theoretical methodology for thermochemical non-equilibrium flow modeling

3.1. Thermodynamic relations and transport properties

The specific total energy of gas mixture etois given as follows24:

where et，s，er，s，ev，sand ee，sare the specific translational energy,specific rotational energy,specific vibrational energy and specific electronic energy of species, respectively. Tt，Tr，Tvand Terepresent the translational temperature,rotational temperature,vibrational temperature and electronic temperature of system states,correspondingly.，ρsand usare the heat of formation,density and velocity of species.R is the universal gas constant,and Msis the molecular weight of species.ε is the degree of rotation freedom,ε=0 is for the monatomic atoms,ε=2 is for the diatomic and linear polyatomic molecules,and ε=3 is for the nonlinear polyatomic molecules.Nvis the number of degenerate modes for vibrational energy,gv，s，irefers to the species degeneracy of vibrational mode i,and θv，s，irepresents the species characteristic temperature of vibrational mode i. Neis the number of degenerate modes for electronic energy,ge，s，irefers to the species degeneracy of electronic mode i,and θe，s，irepresents the species characteristic temperature of electronic mode i.

According to Eucken’s semi-empirical formula25, the species translational thermal conductivity κt，s, the species rotational thermal conductivity κr，s, and the species vibrational thermal conductivity κv，scan be written as

The species viscosity coefficient μsis calculated by using Gupta-Yos’s curve-fitted temperature function8as follows

where Aμ，Bμand Cμare constants determined by each species listed in Table 1.The applicable temperature range of the function above is 1000 K ≤T ≤30000 K.

In addition, after getting the transport properties of different species, the mixture viscosity coefficient μ, the mixture translational thermal conductivity κt, the mixture rotational thermal conductivity κrand the mixture vibrational thermal conductivity κvcan be calculated by using Wilke’s mixing rule26, respectively.

In order to calculate the species diffusion coefficient Ds，the following formula is used for atoms, molecules and ions:

The diffusion coefficient of electrons is calculated by:

where Xsis the species mole fraction, Meis the molecular weight of the electron. Sc is the Schmidt number, Sc=0.5 is for atoms and molecules, and Sc=0.25 is for ions.24

Table 1 Constants for viscosity coefficient curve fits.

3.2. Chemical reaction model

The general expression of a common chemical reaction equation can be written as

where r=1,2,...,Nr,and Nris the number of chemical reactions. S1, S2,..., Snare different kinds of species. αs，rand βs，rare the stoichiometric coefficients of species in the rth forward and backward reactions, respectively.

The mass formation rate of species ˙ωsis given as follows

where Ss［ ］ is the species molar concentration, Rf，rand Rb，rare the forward and backward reaction rates, respectively.

Therefore, the calculation equation of ˙ωscan be obtained by combining Eqs. (20) and (21) as follows

The forward reaction rate coefficient Kf，ris determined by Arrhenius formulas27as

The backward reaction rate coefficient Kb，rcan be calculated by either Arrhenius formulas or the equilibrium constant Keq，r. Gupta et al.’s8least-squares curve fit of the equilibrium constant Keq，ris chosen to calculate Kb，ras follows

where a1，r，a2，r，a3，r，a4，r，a5，rand a6，rare the curve fit coefficients affected by the number density of particles given in Ref.8.Afis the pre-exponential parameter,Bfis the temperature exponent and Cfis the activation temperature, and they are constants related to each chemical reaction.

The high temperature air after shockwave is treated as a mixture of 11 species (N2, O2, NO, O, N, NO+, N2+, O2+,N+, O+, e-). The Gupta’s thermochemical non-equilibrium model8is widely used for hypersonic thermochemical nonequilibrium environment simulations. The chemical reactions of dissociation,neutral exchange,charge exchange,associative ionization, electron impact dissociation and ionization are included in the Gupta’s thermochemical non-equilibrium model. The relevant constants for the forward reaction rate coefficients of the Gupta’s chemical reactions are listed in Table 2.

3.3. Temperature controlling

The influence of thermal non-equilibrium states on chemical reactions can be accounted by the chemical reaction rate controlling temperature Tc.The rate controlling temperature Tcof the 11 species chemical reaction model is a function of different temperature modes given by

The rate controlling temperature Tcdepends on the types of chemical reactions, for example, the dissociation and ionization reactions. According to Park’s two-temperature model,the translational energy mode of heavy-particle and the molecular rotational energy mode are in equilibrium in terms of the translational-rotational temperature Ttr. Meanwhile, the molecular vibrational energy, electron translational energy and electronic excitation energy are described by the vibrational-electronic temperature Tve.Therefore,the rate controlling temperature Tccan be written as

where a+b=1,a and b are the coefficients of rate controlling temperature, and they show the importance of different temperature modes on each chemical reaction9. In the present work, referring to the research of Kim et al.28, the coefficients of rate controlling temperature for the forward and backward reactions of various reaction types are listed in Table 3.

3.4. Relaxation time model

The energy transport between the translational mode and vibrational mode et-vis solved by using the Landau-Teller model29as

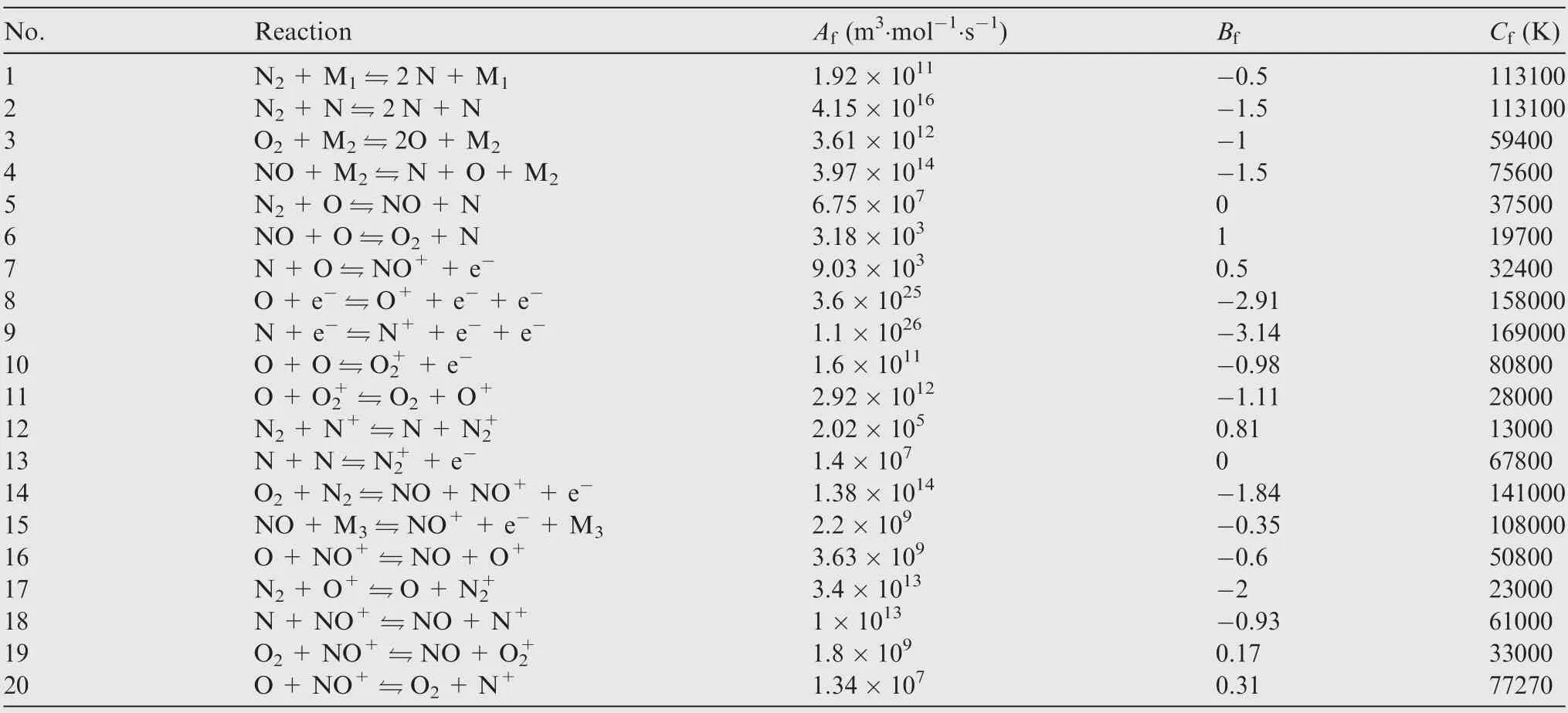
Table 2 Gupta’s chemical reactions.

Table 3 Coefficients of rate controlling temperature for various reaction types.

For the temperature between 3000 K and 8000 K,the characteristic vibrational temperature relaxation time scale of species τv，sis evaluated by the Millikan-White expression30as

For the temperature over 8000 K, τv，scan be calculated by the Park’s correction31given as

4. Validation of method

4.1. Grid independence study in hypersonic environment calculations of a hemisphere

Hypersonic aerodynamic heating numerical results are closely related to the heights of the first grid point off wall32. The hemisphere model33with a diameter of 76 mm is chosen for hypersonic numerical calculation verification. The free stream parameters are as follows:Ma∞=12.4, T∞=535 K and P∞=178.1 Pa. Ma∞, T∞and P∞are the Mach number,temperature and pressure of free stream, respectively. The temperature of the non-catalytic isothermal wall is Tw=300 K. The mass fractions of N2and O2in the free stream are YN2=0.77 and YO2=0.23.The Gupta’s 11 species thermochemical non-equilibrium model is utilized and the HLLC scheme combining with the minmod limiter is taken.

The height of the first grid point off wall nwcalculated by the First Grid Point spacing(FGP)formula34can be expressed as a function of the free stream unit Reynolds number Reu，∞and the free stream Mach number Ma∞as follows:

Another method widely applied to determine the value of nwis the flow cell Reynolds number method35based on the free stream parameters given by

where Recfis the flow cell Reynolds number, V∞， μ∞and ρ∞are the free stream velocity, viscosity coefficient and density, respectively. Numerical results with high accuracy can be obtained by using the value of flow cell Reynolds number Recf= 1 for hypersonic aerodynamic heating environment calculations.

Table 4 lists the heights of the first grid point off wall nwand the distributions of grid nodes of different structured grid models. The heights of the first grid point off wall nwof Grid 1, Grid 2 and Grid 3 models are determined by the flow cell Reynolds number method. Grid 1 model has the value nw= 4.192 × 10-5m using Recf= 10, while Grid 2 and Grid 3 models have the same value nw= 4.192 × 10-6m using Recf= 1. Meanwhile, the value nw= 1.602 × 10-7m for Grid 4 model is determined by the FGP formula. However, Grid 1, Grid 2 and Grid 4 models have the same grid nodes distribution in the tangent and normal directions.

Fig. 1 shows the distributions of Mach number, pressure, translational-rotational and vibrational-electronic temperatures in the flow filed calculated by using Grid 2 model. The high pressures are mainly concentrated in the small area near the stagnation point. Table 4 gives the values of the maximum translational-rotational temperature Ttr，maxand the maximum vibrational-electronic temperature Tve，maxcalculated by using different grid models. The difference between the values of Ttr，maxand Tve，maxcan reveal the degree of thermochemical nonequilibrium of the high temperature flow after shockwave.

Fig. 2 shows the wall pressure distributions calculated by four grid models. φ is the central angle of the hemisphere. Though the heights of the first grid point off wall or the numbers of grid nodes vary greatly, the wall pressure distributions calculated by different grid models are nearly the same. In addition, Table 4 also clearly shows that there is a very small difference in the maximum wall pressures at the stagnation point Pst.

Fig. 3 compares the wall heat flux (q) distributions calculated by different grid models with the experimental data.The maximum wall heat flux at the stagnation point qst=8.89×106W·m-2and the wall heat flux distributions calculated by Grid 4 model are too big, while the wall heat fluxes calculated by Grid 1 model are too small. However,the wall heat flux distributions calculated by Grid 2 and Grid 3 models with nw=4.192×10-6m using Recf=1 are in good agreement with the experimental data. It can be seen that the great difference in wall heat fluxes is mainly caused by the heights of the first grid point off wall nwcalculated by different methods. Although Grid 2 and Grid 3 models have the same value nw=4.192×10-6m,the accuracy of wall heat flux calculated by Grid 3 model is not significantly improved by increasing the number of grid nodes. The maximum wall heat fluxes calculated by Grid 2 and Grid 3 models are only 2.3%less and 1.52% bigger than that measured by the experiment,correspondingly.Therefore,it’s better to improve the accuracy of numerical wall heat flux by using a suitable height of the first grid point off wall instead of only increasing the number of grid nodes for hypersonic numerical calculation.

In general,the influence of the height of the first grid point off wall on numerical wall heat flux is much greater than that of numerical aerodynamic force. What’s more, the theoretical methodology for thermochemical non-equilibrium flow combing with the HLLC scheme is capable of effectively calculating hypersonic thermochemical non-equilibrium environment when Recf=1 is used. Therefore, the height of the first grid point off wall calculated by the flow cell Reynolds number method using Recf=1 is utilized for all the following hypersonic numerical calculations.

4.2. Calculation of thermochemical non-equilibrium flow around a blunt cone

The blunt cone model with a relatively complex aerodynamic shape is chosen as another verification model. The blunt cone model36consists of three parts, namely the forebody, afterbody and cylindrical sting. The angle of the forebody is 140°,the nose radius is Rn=38.1 mm, and the base diameter is Db=76.2 mm. The length and diameter of the cylindrical sting are 221 mm and 19.1 mm, respectively. The radius of the circumference between the forebody and afterbody is 3.82 mm.The sting and the afterbody are connected by a junction with the radius of 6.35 mm. Table 5 lists the free flow parameters. Re∞is the free stream Reynolds number, XN2and XO2are the mole fractions of N2and O2in the free stream.The temperature of the non-catalytic isothermal wall is Tw=295 K. The Gupta’s 11 species thermochemical nonequilibrium model is utilized. The HLLC scheme combining with the minmod limiter is used and the S-A turbulence modelis taken. Fig. 4 shows the grid model with 332×160 nodes in the tangent and normal directions.

Table 4 Numerical results calculated by different grid models.

Fig.1 Distributions of aerodynamic parameters calculated by using Grid 2 model.

Fig.2 Wall pressure distributions calculated by different grid models.

Fig.3 Wall heat flux distributions calculated by different grid models.

Fig.5 gives the Mach number distribution around the blunt cone model.A vortex is generated in the low pressure flow field near the afterbody when the high pressure air flows through the circumference. With the weakening of flow disturbance along the flow direction,the flow Mach number increases near the tail of sting.

Fig. 6 shows the distributions of pressure and temperature in the flow field. It can be seen that the big pressures and high temperatures in the flow field are mainly concentrated in the region near the forebody. The flow pressure and temperature are obviously reduced by the expansion of air flowing through the circumference. Because of the interference of the sting, the temperature of flow near the tail of sting increases slightly.

Fig. 7 compares the wall pressures obtained by the HLLC and Roe’s FDS(Flux Difference Splitting)schemes.Λ is the distance along the contour of model.The reference pressure at the stagnation point is Pst=8.08×104Pa given in Ref.36.The significant decrease in the wall pressure near the circumference is caused by the expansion of high pressure air.It can be seen that the difference between the wall pressures on the forebody calculated by the two schemes is not obvious.Although the pressures on the sting calculated by the HLLC scheme are smaller than those calculated by the Roe’s FDS scheme, the pressures in the region are still very small and not so important.Therefore,the difference in the wall pressures calculated by the two schemes is very small.The wall pressure can be effectively calculated by the HLLC and Roe’s FDS schemes.

Fig. 8 compares the distributions of wall heat flux calculated by the HLLC and Roe’s FDS schemes with the experimental data. The wall heat flux of the tail of sting increases due to the interference of the sting.The reference wall heat flux at the stagnation point measured by the experiment is qst=3.64×106W·m-2.The wall heat fluxes at the stagnationpoint calculated by the HLLC and Roe’s FDS schemes are 2.47% and 17.03% less than the reference heat flux qst, correspondingly. When Λ/Rn∈[0, 1.8), the wall heat fluxes calculated by the HLLC scheme are bigger than those calculated by the Roe’s FDS scheme,but more consistent with the experimental data. When Λ/Rn∈[1.8, 2.1), the wall heat fluxes calculated by the Roe’s FDS scheme are much bigger than the experimental data.It can be seen that the HLLC scheme is better than the Roe’s FDS scheme for hypersonic numerical calculation of wall heat flux. In general, the theoretical methodology for thermochemical non-equilibrium flow combing with the HLLC scheme can also effectively calculate the hypersonic thermochemical non-equilibrium environment of a complex aerodynamic shape.

Table 5 Free flow parameters for blunt cone.

Fig.4 Computational mesh of blunt cone.

Fig.5 Mach number distribution around blunt cone.

Fig.6 Distributions of pressure and temperature in flow field.

5. Numerical study of hypersonic thermochemical nonequilibrium environment for an entry configuration

The entry configuration is an experimental sphere-cone model37derived from the geometry of Mars Environmental Survey vehicle (MESUR). Fig. 9 shows that the half angles of the forebody and afterbody are 70° and 40°, respectively.The base diameter is Db=152 mm and the nose radius is Rn=38.1 mm. In addition, the corner-to-base radius ratio is Rc/（0.5Db）=0.0143,and Rcis the corner radius.Table 6 lists the free flow parameters for the entry model. The computational meshes of the full-mode and half-mode of the entry configuration for different calculations have 210×320 and 210×160 nodes in the tangent and normal directions,respectively.

5.1. Influence of ionization on shock stand-off distance

The Mach number distributions in the flow field calculated by different gas models at angle of attack α=0°are compared in Fig.10.The temperature of the non-catalytic isothermal wall is Tw=300 K. The perfect gas model doesn’t consider any chemical reactions in hypersonic flow. The 5 species (N2, O2,NO,O,N)model only considers the first four sets of dissociation reactions and the next two groups of exchange reactions in Table 2, but it doesn’t take into account the other ionization reactions.

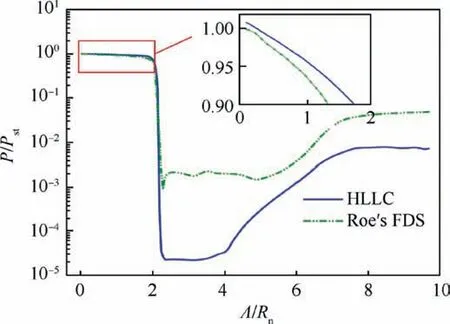
Fig.7 Wall pressures calculated by different schemes.

Fig.8 Wall heat fluxes calculated by different schemes.

Fig. 10 clearly shows that the shock stand-off distance calculated by the 11 species model considering ionization reactions is much smaller than that calculated by the perfect gas model. However, the difference between the shock stand-off distances calculated by the 11 species model and the 5 species model without considering ionization is not obvious. Therefore, the shock stand-off distance of the entry configuration can be reduced by thermochemical reactions but doesn’t continue to decrease remarkably when the influence of ionization is considered.

The shock stand-off distance is related to many factors38,39,such as the flow velocity, the dissociation level of free stream,etc. In addition, the shock stand-off distances in various flow environments also have different relationships40,41. According to the theory given by Hornung and Wen41, the shock standoff distance Δ in hypersonic thermochemical non-equilibrium flow has the relationship as follows:

Fig.9 Geometry of entry model.

Fig. 11 gives the density ratios ρ/ρ∞obtained by different gas models along the stagnation point line. The increase of density ratio after shockwave caused by chemical reactions leads to smaller shock stand-off distances than those are calculated by the 11 species and 5 species models. In addition, the density ratio immediately after shockwave obtained by the 11 species model is ρsh/ρ∞= 6.18 while that obtained by the 5 species model is ρsh/ρ∞= 6.06. Furthermore, a bigger value of density ratio ρsh/ρ∞will lead to a smaller shock stand-off distance. Therefore, the normalized shock stand-off distance Δ/D (D= 76.2 mm) of the entry configuration calculated by the 11 species model is Δ/D = 0.225, which is 28.8% and 4.2% smaller than that calculated by the perfect gas model and the 5 species model, respectively. Because of the higher temperatures required for ionization reactions, the quantity of ionization reactions is relatively less than those of dissociation and exchange reactions. As a result, the products of ionization reactions don’t cause a significant increase in the mixture density after shockwave. In conclusion, the shock stand-off distance can’t be reduced obviously by ionization reactions.

5.2. Influence of ionization on hypersonic aerodynamic and aerothermal loads

The mole fractions of different ionized species and electrons around the entry configuration at α =0° are shown in Fig. 12. The mole fractions of N2+, O2+, N+, O+and e-in the flow field vary greatly, which is mainly caused by the various onset temperatures and quantities of ionization reactions when they are produced. As there are many groups of ionization reactions in Table 2 to produce large quantities of electrons, the maximum mole fraction of e-shown in Fig. 12(a) is Xe-= 5.775 × 10-6that is bigger than those of other ionized species. The maximum mole fraction of N+is XN+= 4.505 × 10-11that is the smallest due to the very high temperature required for its formation.

The mole fractions of various neutral species along the stagnation point line calculated by different species models are compared in Fig. 13(a). Because of the temperatures required for the chemical reactions of O2dissociation and NO formation are lower than those required for other chemical reactions, the maximum mole fractions of the products O and NO are relatively bigger. However, as ionization reactions consume part of the internal energy to produce electrons and ions and also reduce the flow temperature after shockwave, the reductions of N2and O2as well as the productions of O, NO and N calculated by the 11 species model are smaller than those calculated by the 5 species model. Fig. 13(b) clearly shows thatthe mole fractions of e-,NO+and O2+are bigger than those of other ionized species along the stagnation point line, which is caused by the larger quantity of ionization reactions to produce e-and the lower temperatures required to generate NO+and O2+.

Table 6 Free flow parameters for entry model.

Fig.10 Mach number distributions calculated by different gas models at α=0o.

Fig.11 Density ratios along stagnation point line at α=0o.

Fig. 14 gives the temperature distributions calculated by different gas models. As chemical reactions such as dissociation, exchange and ionization reactions consume lots of internal energy,the flow temperature after shockwave decreases.As a result, the distributions of different temperatures calculated by the two kinds of species models considering chemical reactions, on the whole, are smaller than the distribution of static temperature calculated by the perfect gas model. In addition,Fig. 14 shows that the maximum translational-rotational and vibrational-electronic temperatures calculated by the 11 species model are slightly smaller than those calculated by the 5 species model. It can be explained that the quantity of ionization reactions is less than that of dissociation and exchange reactions due to their higher onset temperatures, which makes the internal energy consumption of ionization reactions less and does not lead to a significant decrease in temperature.

Fig.15 gives the distributions of wall pressure computed by different gas models at α=0°.The maximum pressures at the stagnation point calculated by the perfect gas model,the 5 species and 11 species models are 5.236,5.282 and 5.3 kPa,respectively. The maximum pressure calculated by the 11 species model is only 1.22% and 0.34% bigger than that calculated by the perfect gas model and the 5 species model,respectively.As is well known that the gas pressure P=NkT is proportional to the number of particles per unit volume N when the temperature T is set to a constant.Although chemical reactions including ionization reactions produce new species,there are still many groups of reactions in Table 2 fail to change the number of particles per unit volume, such as NO+O ⇋O2+N and O+O ⇋O2++e-. In addition, ionization reactions produce large quantities of electrons, but the change of pressure caused by electrons is very limited due to the small mass of an electron. Therefore, ionization reactions can increase wall pressure but the increment is very small.

Fig.16 compares the wall heat fluxes calculated by different gas models with the experimental data. The maximum wall heat flux measured by the experiment is 7.7×105W·m-2.The maximum heat flux at the stagnation point calculated by the 11 species model is 7.83×105W·m-2, which is 14.71%and 4.4%smaller than that calculated by the perfect gas model and the 5 species model, respectively. The error between the maximum heat flux calculated by the 11 species model and that measured by the experiment is 1.7% which is the smallest.What’s more,although the distribution of wall heat flux calculated by the 11 species model is lower than those calculated by the perfect gas and 5 species models,it is more consistent with the experimental data.However,the numerical heat fluxes out of the range x=-30-30 mm are bigger than the experimental data, which is mainly due to the small height of the first grid point off wall nw=9.16×10-6m. Although the total heat flux is composed of different kinds of energy flux, it is greatly affected by the thermal conduction heat flux.According to the classical Fourier law, the thermal conduction heat flux is related to the gradients of different temperatures including the translational-rotational and vibrational-electronic temperatures. However, the two kinds of temperatures calculated by the 11 species model are smaller than those calculated by the 5 species model, which results in a smaller wall heat flux obtained by the 11 species model. Therefore, ionization has great influence on wall heat flux and should be seriously considered.

Fig.12 Mole fractions of different ionized species and electrons in flow field at α=0o.

5.3. Effect of wall catalysis on hypersonic ionized flow environment

The mass formation rate of species due to the catalytic activity at the wall ˙ωc，shas the following relationship42

where Dw，sand （∂Ys/∂n）ware the diffusion coefficient and mass fraction gradient of species at the wall, respectively.

Three different catalytic wall conditions are considered in this study, namely the non-catalytic wall, super-catalytic wall and partially catalytic wall conditions.

(1) Non-catalytic wall

There are no chemical reactions at the non-catalytic wall.Therefore, the mass formation rate of species at the wall is ˙ωc，s=0, namely,

(2) Super-catalytic wall

The chemical reactions at the wall are assumed to be catalyzed at an infinite rate. It is not a real existence but an extreme case assumed.The mass fraction of species at the wall Yw，sis equal to its mass fraction in the free flow Y∞，sas follows

(3) Partially catalytic wall

Fig.13 Mole fractions of different species along stagnation point line at α=0o.

Fig.14 Temperature distributions along stagnation point line at α=0o.

For the partially catalytic wall,the chemical reaction at the wall is assumed to be catalyzed at a finite rate. The catalysis mechanism of the partially catalytic wall is very complex. In order to research the effect of wall catalysis on the electrons and ions in hypersonic ionized flow,the electrons and ions(e-,N2+, O2+, NO+, O+, N+) at the wall are assumed to be fully catalyzed at an infinite rate, while the neutral species (N2,O2, NO, O, N) are not considered to be catalyzed at the wall.The chemical reactions occurring on the surface of a vehicle(s)caused by the wall catalysis at the partially catalytic wall condition are given as follows

Fig.15 Wall pressures computed by different gas models at α=0o.

Fig.16 Comparison of numerical wall heat fluxes with experimental data at α=0o.

Fig. 17 shows the distributions of Mach number, pressure,translational-rotational and vibrational-electronic temperatures in the hypersonic ionized flow field calculated at the non-catalytic isothermal wall condition (Tw=300 K).Because of the angle of attack α=10°,the pressures and temperatures of flow in the windward area are bigger than those in other areas.

Fig. 18 gives the wall pressures calculated at the Non-Catalytic (NC), Partially Catalytic (PC) and Super-Catalytic(SC) wall conditions. Both the maximum wall pressures and the distributions of wall pressure are nearly the same at different catalytic wall conditions.It can be clearly seen that there is no remarkable change in wall pressure when the effect of wall catalysis is considered.Because there are small changes in both the quantity of species and the flow temperature near the wall caused by the wall catalysis, the wall pressure doesn’t significantly change.

Fig.17 Distributions of aerodynamic parameters in flow field at α=10o.

Fig.18 Distributions of wall pressure at different catalytic wall conditions at α=10o.

Fig.19 compares the wall heat fluxes calculated at different catalytic wall conditions with the experimental data. The distributions of numerical wall heat flux are similar to the experimental data. However, the wall heat fluxes calculated at the partially catalytic and super-catalytic wall conditions are bigger than the experimental data when the effect of wall catalysis is considered. As a certain amount of internal energy is generated by recombination reactions, the gas temperature near the wall will increase when the species at the wall are catalyzed. As a result, the wall heat flux will increase but not too much due to the wall catalysis.Moreover,with the increase of wall temperature, the wall heat fluxes calculated at the partially catalytic and super-catalytic wall conditions decrease gradually. This phenomenon is mainly caused by the smaller flow temperature gradient near the wall when the wall temperature increases. Considering that the wall catalysis at low wall temperature is not obvious, the distribution of wall heat flux calculated at the non-catalytic isothermal wall condition(Tw=300 K) is more consistent with the experimental data.In addition, the maximum wall heat fluxes calculated at the partially catalytic and super-catalytic isothermal wall conditions (Tw=300 K) are 10.6% and 25.4% bigger than the maximum experimental measurement of wall heat flux q=9×105W·m-2,respectively.The maximum wall heat flux calculated at the partially catalytic wall condition is 11.8%less than that calculated at the super-catalytic wall condition because only the electrons and ions at the wall are assumed to be fully catalyzed.In general,the thermochemical reactions of electrons and ions catalyzed at the wall can increase wall heat flux obviously, and the influence of wall catalysis on wall heat flux is much greater than that of wall pressure.

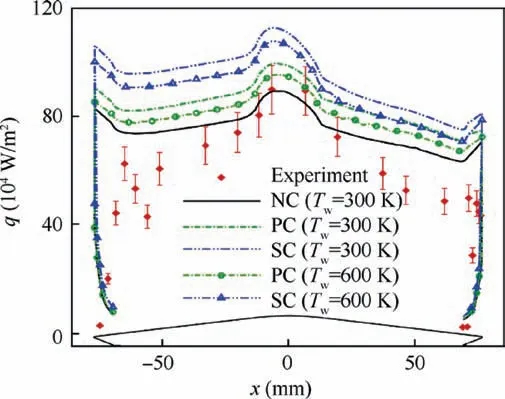
Fig.19 Comparison of wall heat fluxes at different catalytic wall conditions at α=10o.

6. Conclusions

In order to effectively research the hypersonic thermochemical non-equilibrium environment of an entry configuration in ionized flow, a theoretical methodology for thermochemical nonequilibrium flow combing with the HLLC scheme is utilized.The conclusions obtained are as follows:

(1) The theoretical methodology for thermochemical nonequilibrium flow combing with the HLLC scheme is capable of effectively researching hypersonic thermochemical non-equilibrium environments of different aerodynamic shapes including the entry configuration in ionized flows.

(2) The shock stand-off distance of the entry configuration can be reduced by thermochemical reactions but doesn’t continue to decrease remarkably when ionization occurs. The increase of flow density after shockwave caused by ionization leads to a smaller shock stand-off distance. The shock stand-off distance calculated by the 11 species model is 4.2%smaller than that calculated by the 5 species model without considering ionization.

(3) Ionization reduces wall heat flux but increases wall pressure a little. The difference in wall pressures calculated by the 11 species and 5 species models is very small.The wall heat fluxes calculated by the 11 species model are smaller than those calculated by the 5 species model but more consistent with the experiment data.

(4) The thermochemical reactions of electrons and ions catalyzed at the wall increase wall heat flux significantly but make a small change in wall pressure.The effect of wall catalysis on wall heat flux is much greater than that on wall pressure. The maximum wall heat flux obtained by only considering electrons and ions catalyzed at the partially catalytic wall condition is 11.8% less than that calculated at the super-catalytic wall condition.