直齿锥齿轮精确数学建模及其齿面接触分析
2020-01-08芦传洋崔文庆曹雪梅
何 昕 芦传洋 崔文庆 曹雪梅
(1. 黄河水利职业技术学院机械工程学院 河南 开封475000;2. 河南科技大学机电工程学院,河南 洛阳471003)
直齿锥齿轮的齿廓实际上为一球面曲线,微小的加工误差即会对齿轮副的啮合性能产生影响[1-2]。 因此,对直齿锥齿轮建立精确的数学三维模型是分析其承载能力和啮合性能的前提。
文献[3]提出了直齿锥齿轮三维参数化扫描成形建模方法, 通过参数建立球面渐开线和齿根曲线,再由此作出片体,但存在不稳定性误差。 文献[4]在Plo/E 中建立直锥数学模型, 在MSC.Marc 中进行三维弹性有限元模拟,考虑了轮毂下齿轮刚性变化情况,但其所建模型转换过程存在较为明显的误差。文献[5]根据球面渐开线的生成原理,使用Pro/E 软件,采用由线到面再到实体的方式,实现了直齿锥齿轮系建模的精确化与参数化,但整体依托建模软件,缺乏直齿锥齿轮成形原理依据。
本文以刨齿机上刨削直齿锥齿轮为基础,建立直齿锥齿轮齿面方程。基于此,编写齿面点求解程序,利用MATLAB 导出精确齿面点数据,在UG 中生成直锥单侧齿面片, 通过直锥几何原理, 对其单侧齿面片在分度圆上分锥线镜像生成轮齿齿槽, 进而完成直齿锥齿轮精确数学建模。
1.刨齿展成法直锥齿面方程
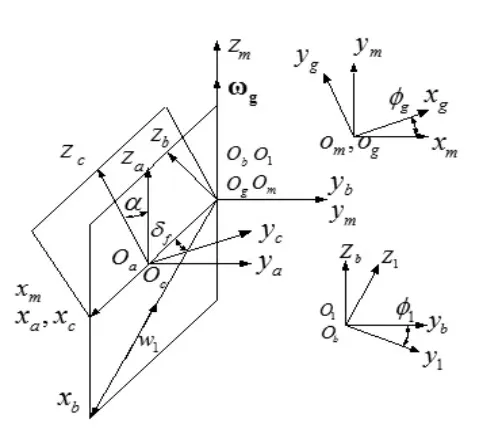
图1 切齿坐标系
直齿锥齿轮的齿形切齿加工一般在刨齿机上通过刨削实现,本文选取一对轮位修正量和床位均为零的直锥齿轮进行实验。 在刨齿机上加工直锥轮坯时,刨刀安装在摇台处刀架上,随摇台做旋转运动产生范成齿形,同时往复直线运动切削轮坯。 刀具刀刃是一条直线,刀具沿着xc方向运动,此时xcoczc为产形面坐标平面。
建立直齿锥齿轮切齿坐标系如图1 示。 图中:α—被加工齿轮的压力角;Φg—摇台转角;δf—被加工齿轮根锥角;Φ1—被加工齿轮转角。
通过求解产形面和被加工齿面之间的啮合方程,可得直齿锥齿轮齿面方程。
2.直齿锥齿轮精确数学建模
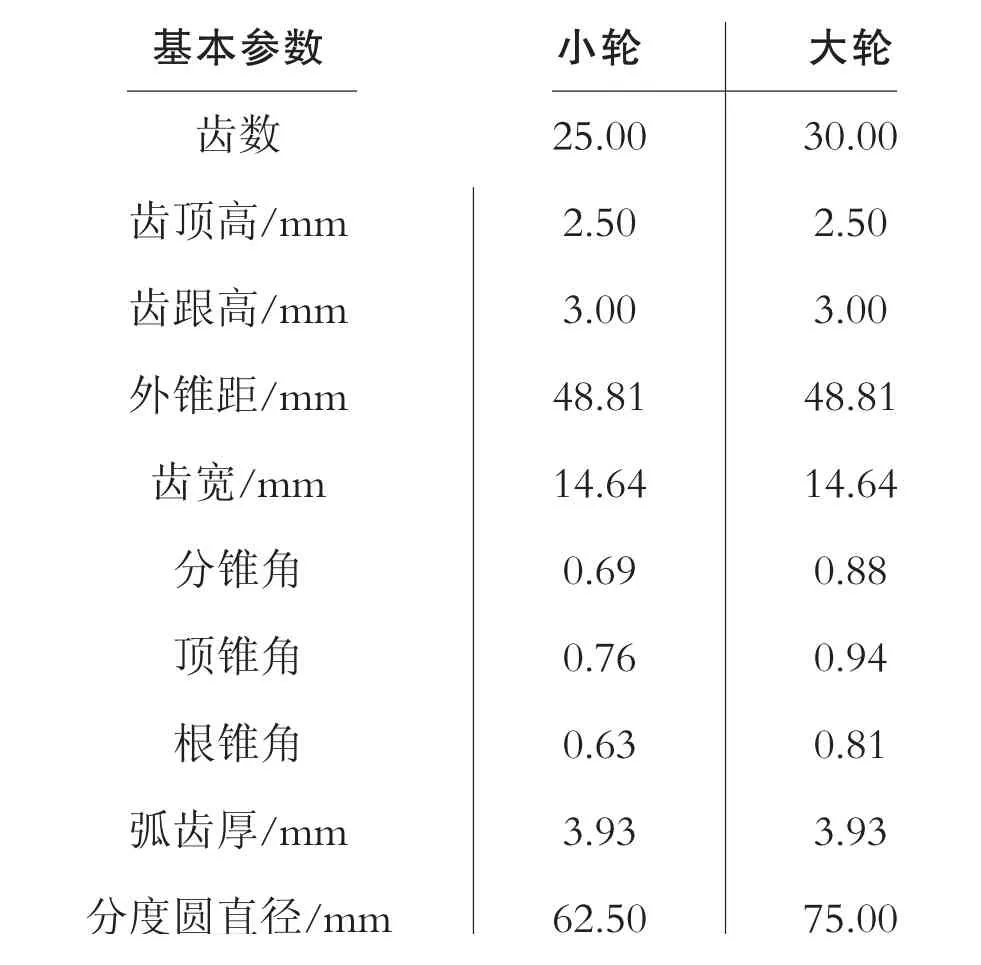
表1 齿轮基本几何参数
在MATLAB 中通过直齿锥齿轮齿面方程导出单侧齿面片齿面点族DAT 文件。 以表1 齿轮副参数进行精确数学建模, 在UG 中生成精确直锥单侧齿面片模型[6-9],如图2 所示。
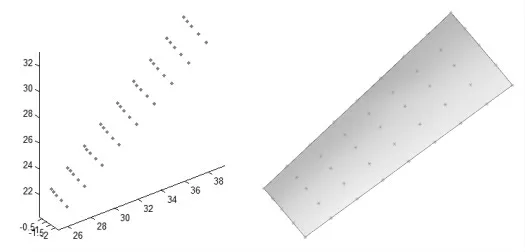
图2 齿面片体
为了建立精确的直齿锥齿轮三维模型, 本文提出了一种基于直锥几何原理的建模方法:根据分度圆上分锥线转动每一度所对应的弧长即分度圆齿厚,求解出两个齿面片之间分锥线所转动角度,由此计算出镜像基准线位置。

式 (1) 中,L 为两齿面片之间分度圆齿厚;N为齿厚所对应圆心角度;S 为每度所对应弧长。
通过选取分度圆上镜像基准分锥线, 对单侧齿面片进行镜像,得到等基圆锥齿轮两侧齿面片。通过MATLAB 可求出另一侧齿面片齿面点族,导入UG 中和镜像齿面完全吻合, 进一步验证了程序和所选镜像基准线的正确性,如图3 所示。
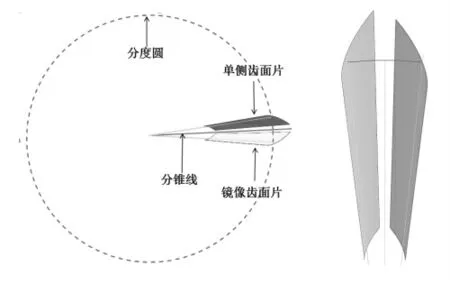
图3 对称齿面片体
此时, 在UG 的建模模块通过对齿面片进行缝合等一系列操作,生成直齿锥齿轮小轮模型,同时对直锥大轮进行三维模型。 对直锥齿轮副进行装配和运动仿真,得到齿轮副虚拟接触区域,如图4 所示建模装配和运动仿真过程。

图4 齿轮副的装配图
在UG 的运动仿真模块, 通过主动轮带动从动轮啮合滚动,调制齿轮显示颜色,可以清晰看出两齿轮齿面间接触印痕,如图5 所示齿轮副虚拟滚检印痕图。
图5 齿轮副虚拟滚检印痕图
3.齿面接触分析
齿面接触分析(TCA)可以模拟滚检时齿面的接触印痕和传动误差,也是分析齿轮实际工况下承载能力、振动噪声的前提。 通过编写直齿锥齿轮齿面接触分析程序,分析其几何传动误差曲线以及齿面接触印痕图形。 通过和虚拟滚检得到的接触印痕相对比进行相互佐证以验证分析结论的正确性[10-13]。
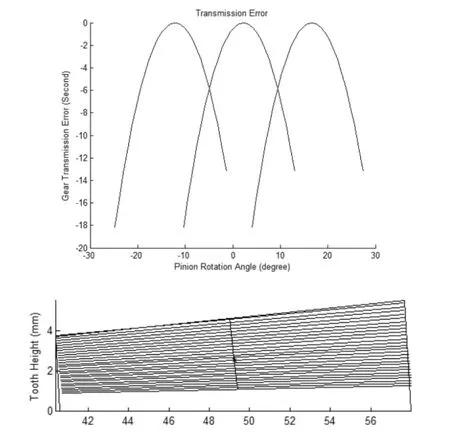
图6 传动误差和齿面接触印痕
从图6 中观察可得:直齿锥齿轮传动误差曲线为开口向下的抛物线,两侧抛物线平滑略不对称;接触迹线上所选取的接触点接触的椭圆长轴近似无穷大,方向沿着其所在的接触线且通过节锥顶点。
直锥齿面为一直纹面,母线通过节锥,在锥齿轮传动时大小轮直纹面的母线相接触,此时接触椭圆长轴应为无穷大,方向沿主、被动轮齿面上接触线方向, 即实验结果满足理论依据。
4.结论
(1)根据刨齿机刨削直锥过程,建立锥齿轮齿面方程,提取齿面点族数据。 基于齿轮几何原理,提出以分度圆上弧齿厚控制理论依据来精确建模,实验表明模型精确无误,理论依据满足建模要求。
(2)对精确建立的齿轮副模型进行虚拟运动仿真,以其虚拟滚检得到的接触印痕和齿面接触分析程序所得接触印痕相对比基本吻合,进一步验证了模型的精确性和本文所提出建立直锥理论方法的正确性。
