自旋轨道耦合二维费米气体的热力学性质

梁成功,张云波

(山西大学理论物理研究所,太原030006)

超冷原子气体由于其相互作用的高度可调控性,为建立和研究各种物理模型提供了重要平台[1-3].基于超冷原子气体研究各种量子系统的新奇热力学性质是当前物理学研究的热点和前沿课题[4-6].各种可观测的热力学参量如密度、压强、等温压缩系数等为研究量子多体系统的各种新奇量子相以及量子相变提供了重要的观测手段.例如:在液体和固体中等温压缩系数用于探测其流动性和刚度;在超冷原子气体中,已经广泛用于探测从正常相到玻色爱因斯坦凝聚、超流到固体相如超固和Mott绝缘的转变;在光晶格超冷原子系统中,用于探测Mott绝缘相变[7-10]、划分超流相和正常相的相边界[11]、观察超导体中的各种拓扑量子相变[12]、判断二维Hubbard模型中相分离和条纹相的形成[13-14].

最近超冷原子气体研究领域的突破性进展是人造自旋轨道耦合的实验实现[15-19].人造自旋轨道耦合是继Feshbach共振技术调节原子间的相互作用[20-21]、光晶格技术实现各种凝聚态物理模型[22-24]之后,超冷原子体系的又一重要调控手段,极大地拓展了超冷原子的模拟范围,为发现新物态和各种奇异量子现象铺平了道路[25-29].先前的研究已经表明,自旋轨道耦合从根本上改变了超冷费米原子系统的热力学性质[30-31].例如由于自旋轨道耦合和塞曼场的共同作用,在玻色-爱因斯坦凝聚(Bose-Einstein condensate,BEC)-BCS(Bardeen,Cooper and Schrieffer)渡越区域等温压缩系数和压强随相互作用强度的变化表现出反常行为,在某一特定的散射长度附近,等温压缩系数出现了急剧增大的共振峰值,压强指数相应地急剧减小.对于连续系统,这一等温压缩系数和压强的反常行为只能出现在无能隙的相[30].而对于晶格系统该反常行为既可以出现在无能隙的相也可以出现在有能隙的相[31].由于上述结果都是针对的三维费米系统,一个重要的问题是对于自旋轨道耦合的二维费米系统,等温压缩系数等热力学参量是否会出现类似的反常行为,等温压缩系数、压强、热力学熵等热力学量在自旋轨道耦合的二维系统中是否会表现出不同于三维系统的新规律.

关于二维费米系统的研究有助于加深对Berezinskii-Kosterlitz-Thouless相变[32]、非传统超导体[33]、石墨烯[34]、拓扑绝缘体材料[35]、拓扑超导和Majorana零模[37-40]等重要前沿科学问题的理解.因而,研究二维自旋轨道耦合费米气体的热力学性质具有非常重要的意义.本文我们将研究二维自旋轨道耦合的均匀费米原子气体的热力学性质.在平均场近似下,通过求解能隙方程和粒子数方程,讨论了自旋轨道耦合和外加塞曼场对等温压缩系数、压强等热力学参量的影响.研究结果表明,在自旋轨道耦合和外加塞曼场的共同作用下,系统的等温压缩系数在BEC-BCS渡越区域表现出类似于三维系统中随相互作用急剧变化的反常行为.跟三维系统明显不同的是,在BEC极限下,二维系统中等温压缩系数基本不随相互作用变化;而三维系统中等温压缩系数随相互作用增强而线性增大.在BEC极限下,我们发现压强基本不随相互作用变化,这跟三维系统中压强跟散射长度成正比有明显不同.对于强自旋轨道耦合的系统,在BEC-BCS渡越区域,我们还观察到压强随塞曼场增大而减小的不同于BCS极限的反常行为.此外,我们还讨论了有限温度下,超流序参、热力学熵随温度的变化规律.一个重要的发现是在超流相超流序参数随自旋轨道耦合强度变化的非单调行为.与此同时,系统的热力学熵在自旋轨道耦合和塞曼场共同作用下,在正常相和超流相表现出完全相反的变化行为.

1 理论模型

均匀的具有Rashba自旋轨道耦合的二维费米气体,其单粒子的哈密顿量为

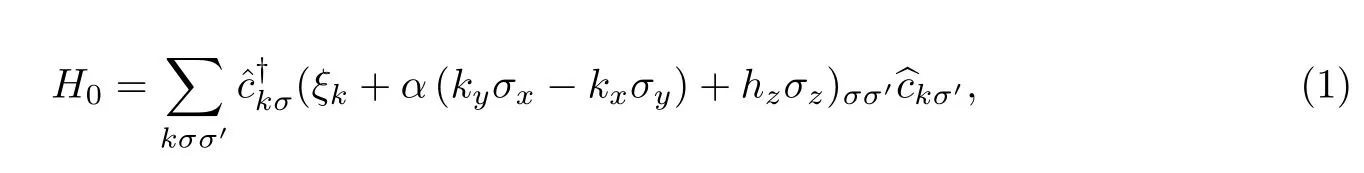
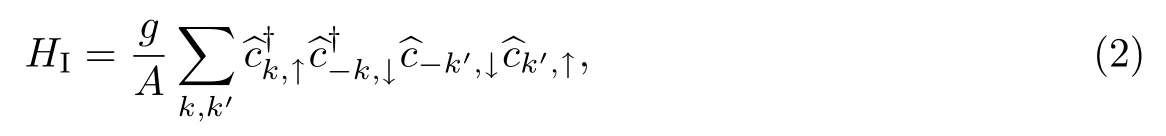
式中:g<0为有效吸引相互作用常数;A=L2,为2D费米气体的面积;对k=(kx,ky)的求和为全空间求和.为避免发散,在2D费米气体中有

应用平均场理论定义序参量,在Nambu-Gorkov自旋基下,其Bogoliubov-de-Genes(Bd G)形式的有效哈密顿量为

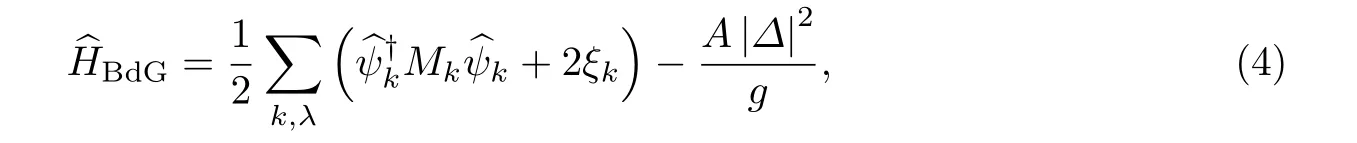
式中,Bd G算符的形式为

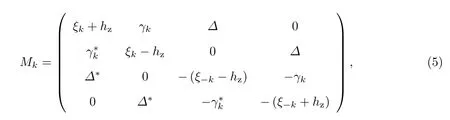
其中γk=α(ky+i kx).做幺正变换使矩阵对角化,可得有效哈密顿量为

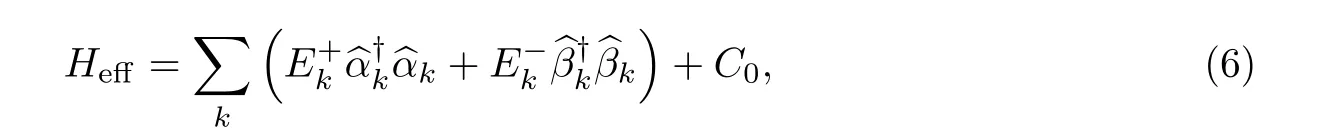
基态能量为

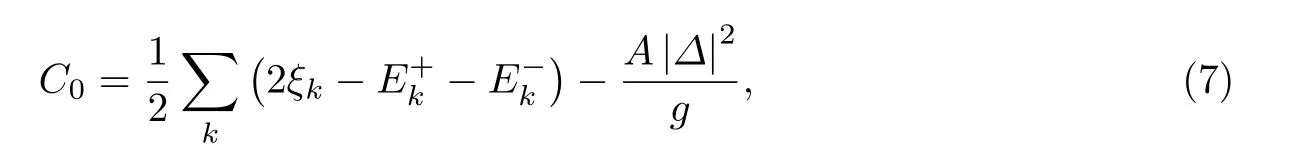
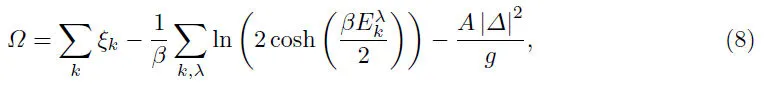
式中,β=1/kBT,kB为玻尔兹曼常数.由∂Ω/∂∆=0,N=−∂Ω/∂µ,可得能隙方程和粒子数方程为

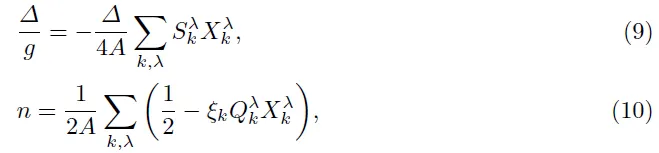
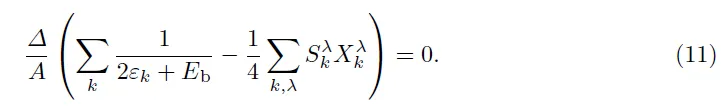
选定费米能EF=(2m)为能量单位,其中二维费米动量=n为原子密度,m为原子质量,这样粒子数密度就为确定量,做无量纲化处理,q=k/kF,求和化积分,在计算中将 q在[−100,100]截断. 通过数值求解方程(10)和方程(11)可以得到超流序参∆和化学势µ,在此基础上可以进一步计算所有热力学量.

2 等温压缩系数和压强

考虑自旋轨道耦合和塞曼场对等温压缩系数的影响.根据Gibbs-Duhem方程和Maxwell关系,等温压缩系数重新定义为

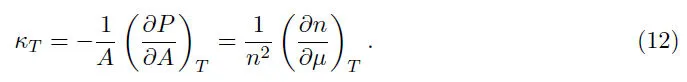
将方程(10)代入式(12),可得二维费米气体的等温压缩系数

对于无自旋轨道耦合的情况,理论和实验研究已经表明二维费米气体与三维相比表现出了完全不同的热力学性质[36].通过自洽求解能隙方程和粒子数方程,可以发现自旋轨道耦合和塞曼场对系统的等温压缩系数有重要影响.

在没有塞曼场的情况下,自旋轨道耦合对二维费米气体等温压缩系数的影响如图1所示.可以看出:当相互作用较弱时(在BCS极限下),随着自旋轨道耦合的增强,等温压缩系数明显增大;当相互作用较强时(在BEC极限下),二维费米系统中的等温压缩系数基本不随相互作用变化.这与三维系统的情况明显不同,因为在三维连续系统中,BEC极限下等温压缩系数随相互作用的增强而线性增大;而在三维光晶格系统中,BEC极限下等温压缩系数随相互作用的增强而线性减小.

在有塞曼场的情况下,通过合适地选择自旋轨道耦合强度和塞曼场的强度,在二维费米系统中观察到先前在三维系统中发现的等温压缩系数随相互作用急剧变化的共振峰[30,31],如图2(a),(b)和(d)所示.可以看出:共振峰的位置主要受塞曼场强度的影响,而基本不随自旋轨道耦合强度改变;而共振峰的振幅受自旋轨道耦合和塞曼场的共同影响.同时,可以发现塞曼场和自旋轨道耦合对共振峰的振幅具有完全相反的效应,即增大塞曼场可以增强共振峰振幅,但增大自旋轨道耦合却可以抑制共振峰振幅,如图2(a)和(d)所示.同样,当自旋轨道耦合强度较弱时,在远离共振峰的位置,等温压缩系数基本不受自旋轨道耦合强度变化的影响,如图2(a)和(d)所示.当自旋轨道耦合强度较强时,等温压缩系数随相互作用变化的共振峰消失,如图2(c)所示.与无塞曼场情况类似,当自旋轨道耦合足够大(相对塞曼场),BCS极限下等温压缩系数随自旋轨道耦合的增强而明显增大,如图2(f)所示.另外,具有塞曼场的自旋轨道耦合系统和无塞曼场的自旋轨道耦合系统,在等温压缩系数方面的另外一个明显不同的特征是,中间强度的自旋轨道耦合(如αkF∼1)在BCS极限会使系统的等温压缩系数明显减小,而不是增大(对比图2(a),(b)中hz=0.6).由图2(b)和(c)还可以看出,在存在自旋轨道耦合的情况下,塞曼场在BEC和BCS极限下对等温压缩系数的影响正好相反.在BEC极限下,等温压缩系数随着塞曼场的增强而增大;而在BCS极限下,等温压缩系数随着塞曼场的增强而减小.

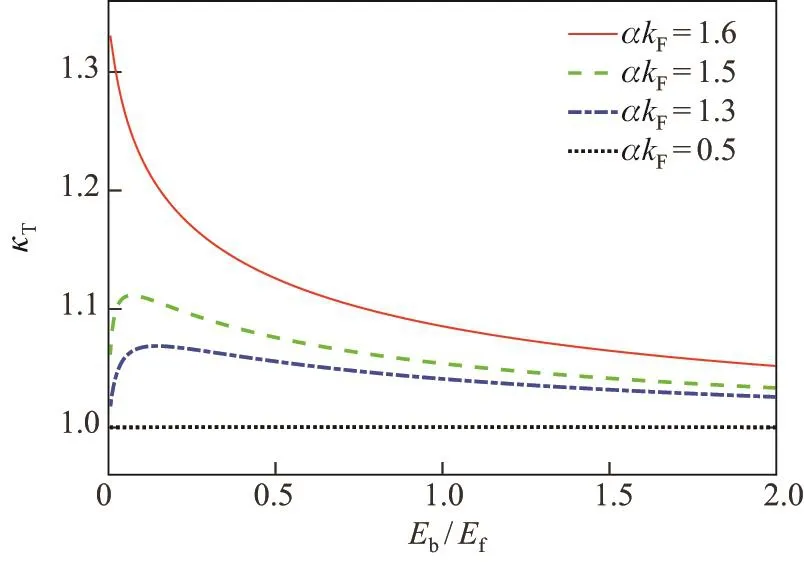
图1 自旋轨道耦合对二维费米气体等温压缩系数的影响(h z=0)Fig.1 Isothermal compressibility as a function of the interatomic interaction strength Eb with the spin-orbit coupling(h z=0)

接下来,讨论在自旋轨道耦合和塞曼场对统计物理中另外一个重要物理量压强的影响.根据压强跟巨热力学势的关系Ω=−PA,通过式(8),可以得到二维费米气体的压强为

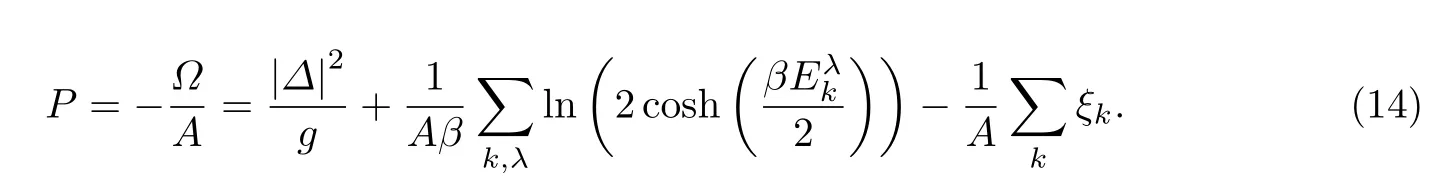
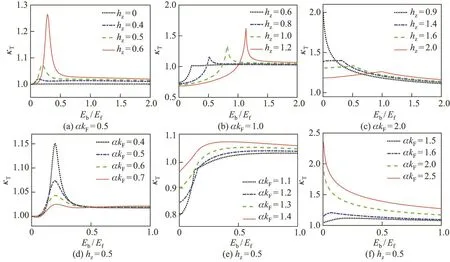
图2 自旋轨道耦合和塞曼场作用下等温压缩系数随原子间相互作用的变化Fig.2 Isothermal compressibility as a function of the interatomic interaction strength with the presence of both spin-orbit coupling and Zeeman field

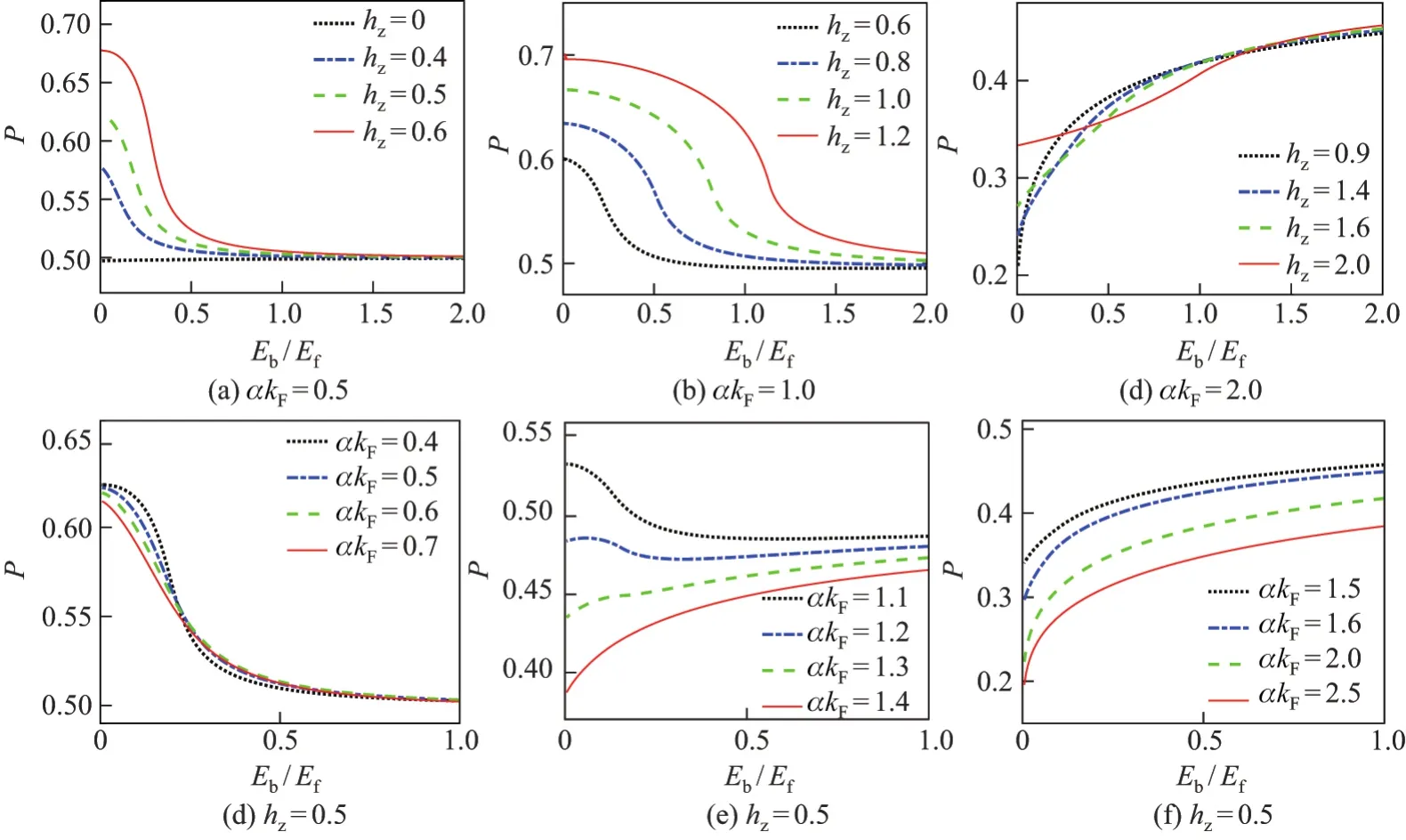
图3 自旋轨道耦合和塞曼场作用下压强随原子间相互作用的变化Fig.3 Pressure as a function of the interatomic interaction strength with the presence of spin-orbit coupling and Zeeman field

由上式可知,系统的压强与二维费米气体的面积成反比,并依赖于序参数∆和化学势µ.仍然考虑平均场近似,在零温极限条件下通过求解能隙方程和粒子数方程得到系统的序参数∆和化学势µ,代入等式(13),可以数值计算系统的压强.在自旋轨道耦合和外加塞曼场共同作用下,压强随原子间相互作用强度的变化如图3所示.可以发现:对于二维费米气体,当存在自旋轨道耦合和外加塞曼场时,在相互作用很强的BEC极限下,系统的压强基本不随相互作用强度的改变而改变.这与三维系统中在BEC极限下,压强与散射长度成正比有明显不同[30].与在BEC极限下的情况明显不同的是,由于自旋轨道和塞曼场的影响,在BCS极限下系统的压强敏感地依赖于系统的相互作用.同时,可以发现增大自旋轨道耦合可以减小压强,如图3(d),(e)和(f)所示.固定自旋轨道耦合强度和原子间相互作用,可以发现在BCS极限下压强随外加塞曼场强度的增加而增大,如图3(a)和(b)所示.对于强自旋轨道耦合的系统,在BEC-BCS渡越区域,还可以观察到压强随塞曼场增大而减小,这是不同于BCS极限的反常行为,如图3(c)所示.

3 热力学熵

众所周知,随着温度的增加,系统会在某一临界温度(超流转变温度TC)时发生从超流相到正常相的转变[18],这一相变现象可以通过超流序参数的变化来刻画.当序参数不为0时,系统处于超流相;当序参数为0时,系统处于正常相.图4给出了在自旋轨道耦合和塞曼场作用下,系统的超流序参数随温度的变化关系.由图4(a)可以看出,当固定塞曼场强度时,超流转变温度随着自旋轨道耦合强度的增大而增大.另外一个重要的发现是,在超流相可以观察到超流序参数随自旋轨道耦合强度变化的非单调行为,即当温度非常小时,在有塞曼场存在的情况下,随着自旋轨道耦合强度从0逐渐增大,超流序参数先减小后增大(见图4(a)).这表明较弱的自旋轨道耦不足以克服塞曼场对超流的抑制作用,整体表现为抑制.当自旋轨道耦合足够大时,自旋轨道耦合的作用占主导,会促进了系统的超流形成.当固定自旋轨道耦合强度时,可以发现超流转变温度随着塞曼场的增大而减小(见图4(b)),这再次表明塞曼场和自旋轨道耦合对超流转变温度的影响正好相反.

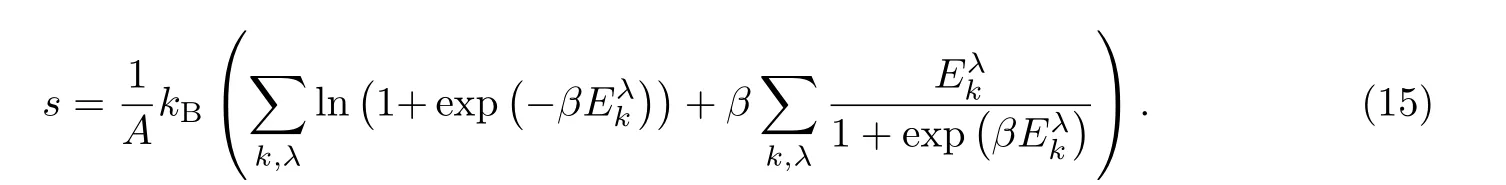
当给定系统的化学势、超流序参数和相互作用等参量时,可以计算系统的热力学熵.接下来主要研究在固定相互作用Eb=1.0的情况下,熵随温度和自旋轨道耦合强度以及塞曼场强度的变化规律.从图4可以看出:在超流转变温度处,熵的一阶导数不连续;在超流相,熵随温度的变化是非线性的,而在正常相,熵随温度的变化是线性的.因此,熵也可以用来表征从正常相到超流相的相变.同时,可以观察到热力学熵在自旋轨道耦合作用下表现出的一些有趣的行为.当自旋轨道耦合较弱时,在某一自旋轨道耦合强度范围内(αkF<0.5)正常相的熵并不随自旋轨道耦合强度的变化而变化(见图4(c));但在相变点附近,由于自旋轨道增强而引起转变温度升高,系统进入超流相,系统突然变得更有序,因而熵随自旋轨道耦合增大而减小.当系统完全处于超流相时,热力学熵随自旋轨道耦合强度的增大而减小,表现出跟正常相完全相反的变化规律(见图4(c)).另外,我们发现当存在自旋轨道耦合时,热力学熵随塞曼场的改变在正常相和超流相也表现出完全相反的变化规律.在正常相,熵随塞曼场的增强而减小;在超流相,熵随塞曼场的增强而增大.这与自旋轨道耦合对熵的影响恰好相反,如图4(d)所示.

4 结束语

本工作应用平均场理论研究了连续系统中自旋轨道耦合和塞曼场共同作用下二维费米气体的热力学性质,并基于平均场理论,通过求解能隙方程和粒子数方程,计算了系统的等温压缩系数、压强、超流序参数和热力学熵.我们发现这些热力学量在自旋轨道耦合和塞曼场作用下,表现出一系列不同于三维系统的新性质:①热力学参量在BEC极限和BCS极限下、在超流相和正常相区域所表现出的对自旋轨道耦合和塞曼场完全不同的依赖关系;②在合适的参数区域各个热力学量随自旋轨道耦合和塞曼场强度的非单调变化行为.所有这些发现为深入理解自旋轨道耦合系统的热力学性质提供了理论依据.需要强调的是,本工作所讨论的热力学量随自旋轨道耦合和塞曼场的变化规律仅限于平均场理论,只适用于温度较低的情况.当温度较高时,尤其对于二维系统由于涨落等因素的影响,本工作所使用的平均理论将不能很好地描述系统真实的热力学性质,需要借助蒙特卡洛数值模拟计算等方法在超越平均场水平上进行研究.

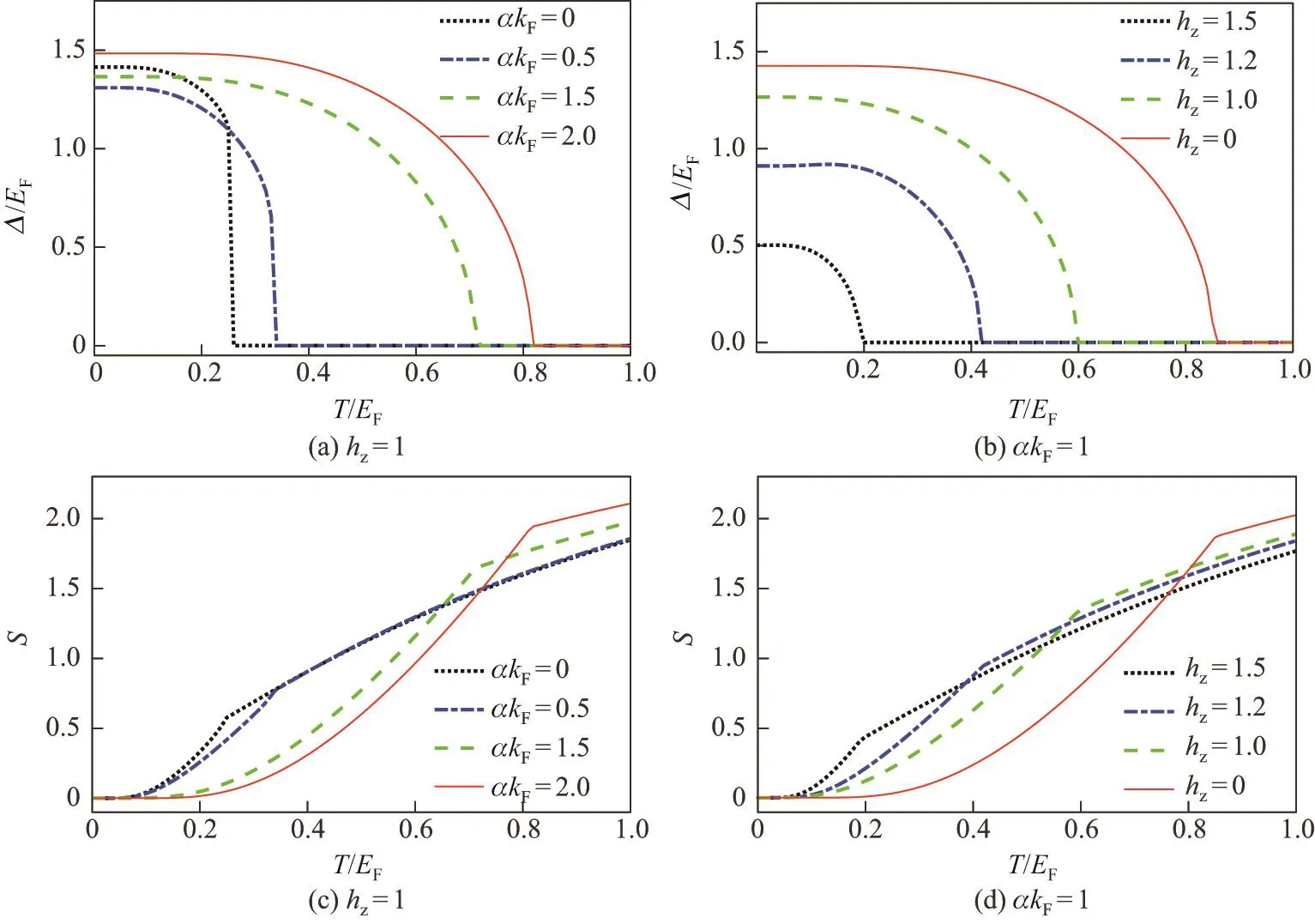
图4 自旋轨道耦合和塞曼场共同作用下序参和熵随温度的变化规律Fig.4 Order parameter and entropy as a function of temperature in the presence of spin-orbit coupling and Zeeman field