一种改进的动力学约束人工势场法

韩知玖, 吴文江,李孝伟, 张 丹,李春欣

(1.上海大学上海市应用数学和力学研究所,上海200072;2.中国舰船研究设计中心,武汉430064;3.上海大学机电工程与自动化学院,上海200444;4.上海大学计算机工程与科学学院,上海200444)

随着无人战斗机在现代战争中扮演越来越重要的角色,路径规划技术受到了国内外学者越来越广泛的关注.路径规划要在地形、威胁、任务执行的时间和协同等约束条件下,实现在任务空间的最优路径,保证无人机(unmanned aerial vehicle,UAV)顺利到达目标[1].

常用搜索最短路径的方法是A*(A-Star)算法和稀疏A*算法,二者均基于栅格化的规划空间模型,通过启发式信息估算下一步前进的最优节点位置,寻找最优路线[2].但是,这类方法过于依赖环境信息,并行性差,计算量大.基于栅格模型,还有各类智能优化算法:Nikolos等[3-4]采用结合了差分进化的遗传算法规划无人机路径,求解速度较快且可以获得多个可行解;Foo等[5]通过粒子群算法求解多无人机的协同三维路径规划问题,效率比遗传算法更高;Roberge等[6]对比分析了遗传算法与粒子群算法,并将二者的优点结合后应用到多无人机的协同路径规划中,获得了一定的可行解.另外,蚁群算法[7]、人工免疫算法[8]和神经网络[9]等智能优化算法,由于具有良好的并行能力,广泛应用于求解路径规划这类计算量较大的问题.

概率图法是将要规划的空间根据约束条件简化成路网图后进行图搜索的一种路径规划方法.常用的概率图算法中,应用于无人机路径规划较多的是Voronoi图法[10],该方法将规划平面的障碍物作为特征元素按照最邻近原则划分后,由连接两邻点直线的垂直平分线组成的连续多边形的网格图.Voronoi图具有计算量小、构造时间快和路径较安全等优点[11],但是由于难以在三维空间中选取特征元素,几乎无法应用于三维的路径规划.

除了上述基于栅格化模型和路网图模型的规划方法之外,1986年Khatib[12]提出了一种比较独特的路径规划方法——人工势场法.人工势场法既不是将规划空间划分为栅格,也不是将规划空间简化成路网图,而是将整个规划空间视为一种虚拟的势场,将无人机在战场环境中的运动抽象为虚拟势场中的运动,即假设目标点对无人机产生“引力”,障碍物对无人机产生“斥力”,最后通过合力引导无人机向势能下降最快的方向前进.采用人工势场法规划的路径比其他基于栅格模型和路网图模型计算的路径更加平滑,计算速度更快,更加适合无人机的路径规划.但是,这种方法有一个致命缺陷,即容易陷入引力和斥力相等的局部极值点,使得算法停滞,无法顺利求解出路径[13].

本工作针对传统的人工势场(artificial potential field,APF)路径规划算法存在局部极小值问题,通过引入虚拟力进行改进,使该算法在考虑控制对象动力运动约束条件下能够快速跳出局部极值.

1 传统人工势场法

1.1 算法模型

人工势场法的实质是对无人机所在区域人为地定义势场,该势场为地图中的障碍物斥力场和目标点引力场的叠加[12].假设无人机的位置为q=(x,y,z),则目标点与无人机的引力场函数为

式中,ξ为引力势场增益系数,qg为目标点的位置.

因此,由式(1)可知引力为

定义第i个障碍物对无人机的斥力势场为

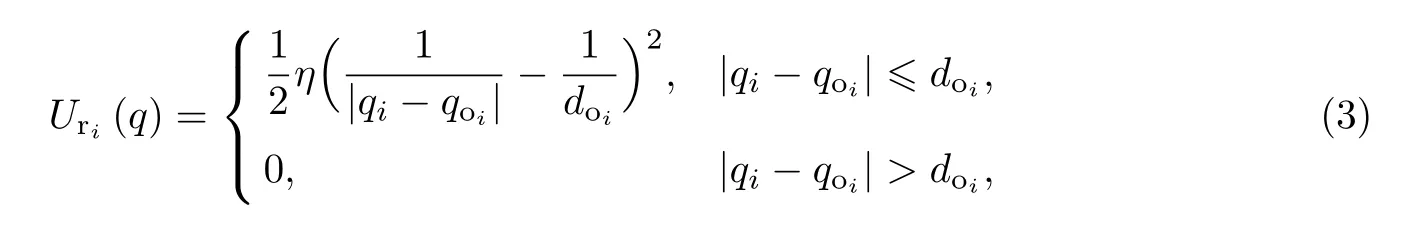
式中,η为斥力势场增益系数,qoi表示第i个障碍物的位置,doi表示第i个障碍物的影响半径.

n个障碍物形成的总的斥力势场为

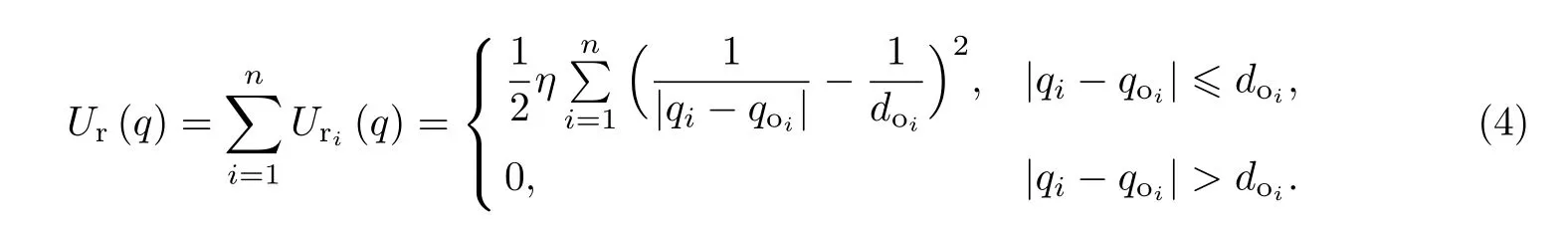
因此,无人机受到的总斥力可为

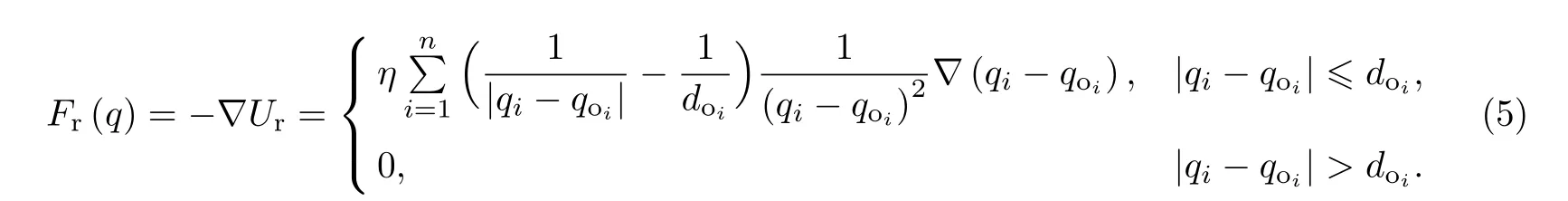
总势场为引力势场和斥力势场的叠加,即有

因此,无人机受到的作用力为

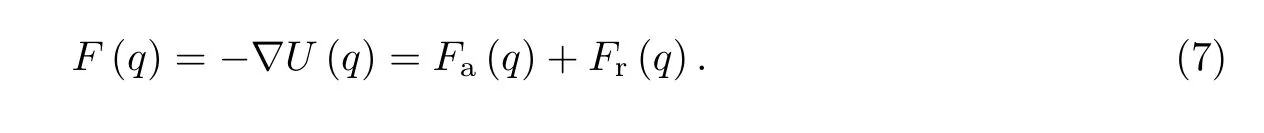
由式(7)可以推断无人机的下一步运动轨迹.

1.2 局部极值问题

采用人工势场法规划的路径较为平滑安全,但在某些特殊点处,引力和斥力刚好大小相等、方向相反,此时无人机容易陷入局部震荡的状况[14].如图1所示,当障碍物在无人机和目标点之间时,人工势场中会形成一个合力为0或接近0的局部极小值点,无人机将在此停止不动或者在附近来回震荡,无法避开障碍物.此时算法停滞,路径规划失败.

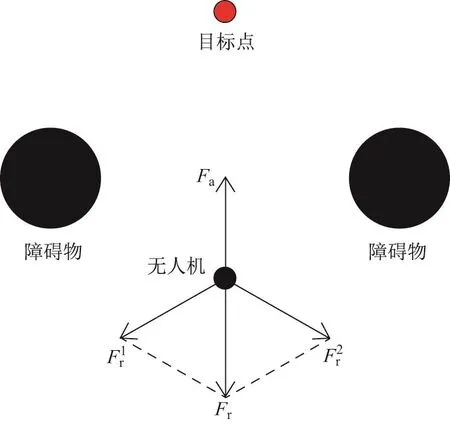
图1 局部极小值点受力示意图Fig.1 Diagram of resultant force at local minima point

考虑到局部极值导致算法停滞的根本原因是受力平衡,本工作提出了一种改进的人工势场法,即当算法陷入停滞时,在人工势场中引入一个作用在无人机上的虚拟力Fs,其方向与斥力垂直,并偏向目标一侧,如图2所示.

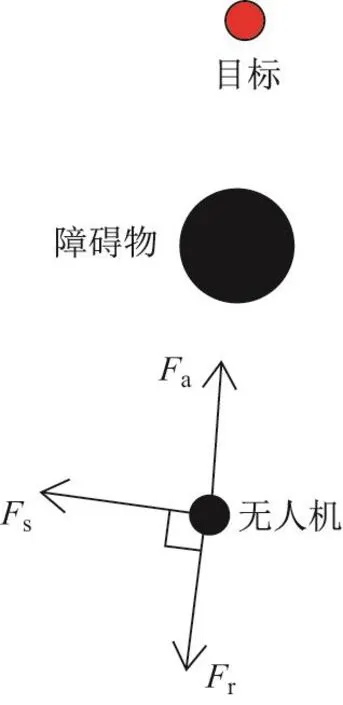
图2 作用在无人机上的虚拟力Fig.2 Swerving force on UAV

虚拟力的大小为

式中,f为虚拟力的增益系数.为了使无人机能够顺利地从凹陷的障碍物中退出来,增益系数需要大于1,因此在本工作中取为2.

虚拟力的方向可以表示为

式中,Fr(q)是所有在影响范围内的障碍物的总斥力.当引力与斥力在同一条直线上时,即Fs(q)Fa(q)=0时,在垂直于斥力的两个方向中随机选择一个作为虚拟力的方向.

为了验证改进的人工势场法可以解决局部极值问题,并能够求解出两点之间的可行路径,本工作在2.2 GHz四核处理器、8 GB内存、操作系统为Windows10的电脑上通过Matlab R2013a模拟仿真了多种地形情况.人工势场法中的基本参数如表1所示,其中Do为引力阈值,l为无人机步长.

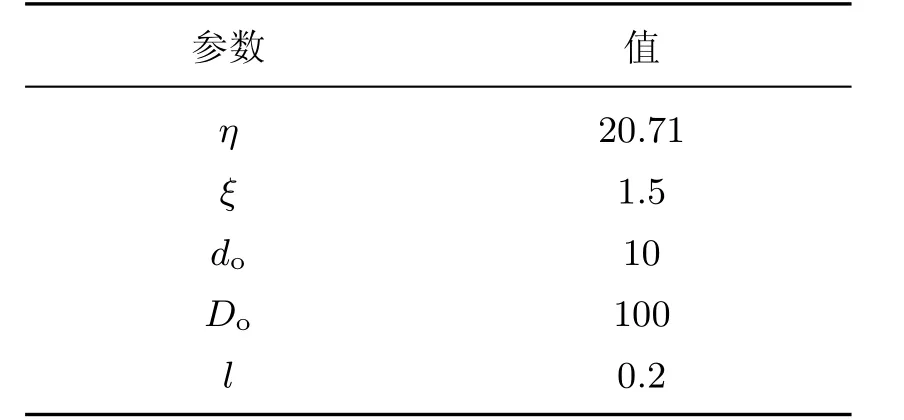
表1 人工势场法的参数设置Table 1 Parameter values of APF algorithm

本工作中路径的起点设为(10,50),终点设为(90,50),通过障碍圆模拟地形中的障碍,其圆心分别为(70,50),(50,35),(50,65),障碍圆半径为5,如图3(a)所示.从图3(a)中可以看出,在由障碍圆组成的地形约束中,传统的人工势场法陷入局部极值困境,无法得到可行路径,而改进后的人工势场法能够成功跳出局部极值,并成功求解得到从障碍物之间穿过的较短路径.

将多个障碍圆叠在一起用来模拟更加复杂的地形.传统人工势场法和改进人工势场法的仿真结果如图3(b)和(c)所示.可以看出:传统的人工势场法在两种情况下均遇到了局部极值问题,没有能够求解出路径;而改进的人工势场法均成功解决了局部极值问题,顺利完成了两种地形下的路径规划.

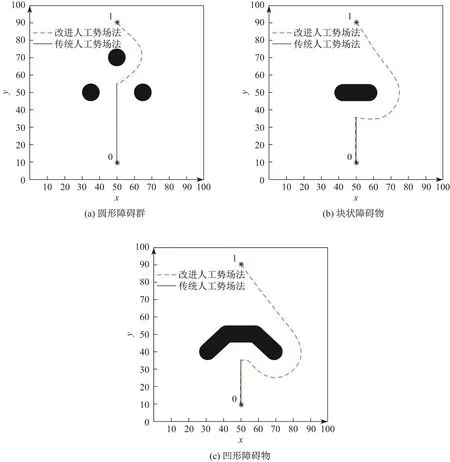
图3 传统人工势场法与改进人工势场法的路径规划Fig.3 Path planning using traditional artificial potential field method and improved artificial potential field method

通过以上算例可以验证:在人工势场中引进虚拟力的方法能够顺利找到两点之间的路径,使无人机成功逃离局部极小值点,绕开障碍物,抵达目标点;在面对复杂的战场情况时,改进的人工势场算法也有较好的表现.

2 动力约束条件分析

考虑到路径规划的结果将用于引导无人机的实际飞行,而实际上固定翼无人战斗机的运动方式,与小型的旋翼无人机或者无人艇、无人驾驶车辆等不同,具有特殊性.因此,本工作针对无人机动力学性能进行了简单的分析.

在实际飞行过程中,随着燃料的不断消耗,无人机的质量并非保持不变.另外,无人机的结构也存在弹性形变.当战场的尺度较大时,整个战场的重力加速度也可能存在变化,甚至地球的自转对无人机的飞行也会有一定影响.对于路径规划问题,将这些因素全部考虑并建立精确的无人机动力学模型是没有必要的,因此,本工作忽略一些次要条件,将无人机近似为质量不变的刚体模型,并且不考虑重力加速度的变化,同时假设无人机在转弯时做协调转弯运动,即转弯过程中无人机偏航角θ持续改变而侧滑角(无人机速度矢量和纵向对称平面的夹角)始终保持为0.

无人机协调转弯时的受力分析如图4所示.由图4(a)可知,无人机竖直方向上的力只有升力的竖直分力和重力.因此,假设滚转角为φ,若保持无人机的高度不变,则有

如图4(b)所示,无人机的向心力由升力的水平分量提供,即

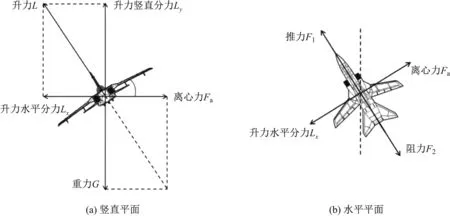
图4 无人机协调转弯时的受力分析Fig.4 Coordinated turning force of UAV

转弯过程中无人机的过载可以表示为

转弯半径可表示为

3 改进动力约束人工势场法

改进的人工势场法虽然能成功地求解两点之间的路径,但是路径在障碍物附近存在比较尖锐的拐角,实际飞行过程中无人机无法按照该路径飞行,因此需要对人工势场法进行优化.

根据无人机转弯时的受力分析可以看出,无人机由于其性能的限制,飞行时转弯半径不能无限小,因此与之相对应的路径也需要限制曲线的曲率半径.图5为相邻路径点的角度差.若限制路径的最小曲率半径(即无人机的最小转弯半径)为rmin,则相邻的3个路径点之间的最大角度差为

当∆θi>∆θmax时,令∆θi=∆θmax,以此来限制路径的曲率半径,使其更加符合无人机的力学性能.

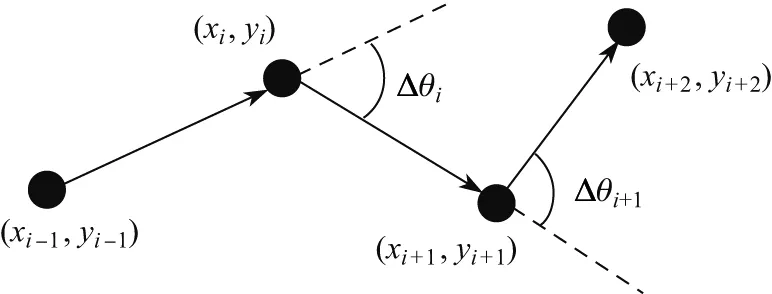
图5 相邻路径点的角度差Fig.5 Angle difference between adjacent path points

为了能够通过仿真算例看出此限制方法的具体效果,假设无人机的最小转弯半径为5(与障碍物半径一致),即角度差限制为0.04.将优化后的路径与图3中未优化的路径进行对比,结果如图6所示.从图6中可以看出,增加了角度差限制的路径在弯曲时比没有增加限制的路径更加圆滑,更加符合无人机的实际性能.虽然优化后的路径距离障碍物更近,牺牲了一定的安全性,但此时尚在安全范围之内,并且人工势场法的优点之一就是可以通过调节障碍物的斥力影响范围来随意调节路径点与障碍物之间的最小距离.

为了进一步验证此方法的可行性,通过障碍圆模拟更加复杂和接近实际的地形,并通过增加角度差限制后的人工势场法求解路径.由于设置的障碍物中,两个障碍物之间的最小距离约为12,为了使路径能顺利地从障碍物之间穿过,障碍物的影响半径do调至6.仿真结果如图7所示.由图7可以看出,在通过障碍圆模拟的复杂地形下,增加了角度差限制的改进人工势场法仍然具有较好的效果,能够顺利求解出两点之间的较短路径,并且同时兼顾了圆滑和安全性.这表明此种改进人工势场法完全可以用于固定翼无人战斗机的路径规划.

4 结束语

本工作对传统人工势场法的不足进行了分析,并重点研究了局部极小值的问题,通过在人工势场中引进虚拟力的方法,使算法能够成功求解出各种复杂障碍下的最优路径.另外,对无人机的动力学性能进行分析,在求解过程中添加角度差限制,通过调节斥力影响半径,使路径能够兼顾距离的长短、曲线的平滑和安全性.仿真实验验证了改进的动力约束人工势场法的有效性,可用于固定翼无人战斗机的路径规划.

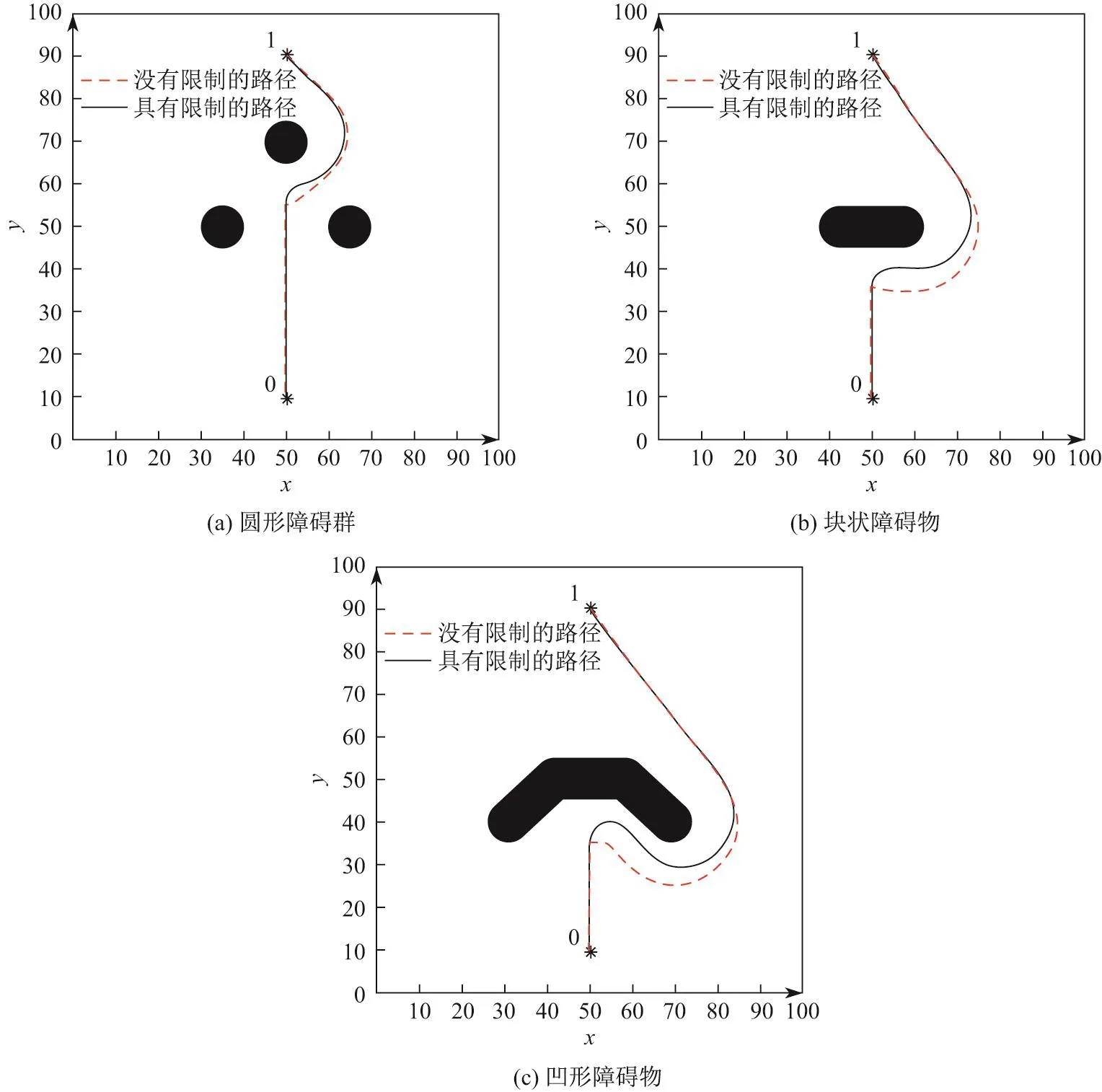
图6 具有限制和没有限制的人工势场法路径规划对比Fig.6 Simulations of path planning using APF method with and without constraint

图7 真实地形下具有限制的人工势场法路径规划仿真Fig.7 Simulation of path planning using constrained APF method under real terrain