碳纤维立体织机平行打纬机构设计与优化

2020-01-08杨建成弭俊波路阳阳许宝勐

天津工业大学学报 2019年6期

杨建成，弭俊波，路阳阳，许宝勐，李笑

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津 300387）

碳纤维立体织物包含碳纤维多层织物及碳纤维中空织物，随着社会的进步及科技的不断发展，碳纤维立体织物在航空航天、船舶、新型汽车、建筑等方面的应用越来越广泛[1-2]。碳纤维立体织机是碳纤维立体织物织造的专用设备，而打纬运动是织机五大运动之一，打纬是织物形成的关键环节，由钢筘将纬纱打入织口。传统打纬机构常采用连杆式或共轭凸轮式[3-5]，钢筘安装在摆臂筘座脚上，钢筘与摆臂同步绕摆臂摆动中心做轨迹为圆弧的运动。共轭凸轮打纬机构适用于高速织机，有学者对传统共轭凸轮打纬机构进行了柔性动力学分析，为高速打纬机构的设计及优化奠定了基础[6]，袁汝旺等[7]考虑经纱受力一致性要求对碳纤维多层织机轴向六连杆机构进行了运动学分析与尺度综合优化设计。但传统打纬机构无论连杆式还是共轭凸轮式都不适于碳纤维立体织物的织造，因该织物自身结构特点使得织物厚度可能远大于普通织物，若碳纤维立体织机钢筘仍做摆动运动，打纬时碳纤维立体织物不同层纬纱受力将不均匀，无法保证使每层纬纱顺利进入织口，这就大大降低了碳纤维立体织物的品质。为实现平行打纬，国内外学者给出了不同解决方案，比如：Badawi[8]提出利用气缸的直线运动来实现钢筘的水平打纬，优化传统四杆机构的结构尺寸，确定最佳的打纬力[9]和机构效率[10-12]，毛莹等[13]给出了打纬机构刚体动力学平衡优化解决方法，但由于气缸的驱动力不易控制，冲击较大且动态响应较慢，不利于碳纤维织物的生产；国内有学者提出用四连杆结合曲柄滑块的组合机构实现平行打纬[14]，这种方案实现了平行打纬，且通过优化各杆件之间的尺寸关系可以得出比较适宜的打纬运动规律，但这种方案存在打纬力不足等问题；平行打纬机构还有增力机构、正弦机构和导杆机构串联的六杆机构等[15]，虽然解决了平行打纬的问题，但存在机构振动大、速度慢等缺点。也有学者对凸轮机构的廓线进行了优化设计[16-18]，但对于共轭凸轮四连杆组合打纬机构的研究较少。本文针对上述打纬机构在碳纤维立体织物织造中的不足，提出共轭凸轮四连杆组合式打纬机构，并对其进行运动学分析和优化，以提高碳纤维立体积物的产品质量。

1 工作原理

基于以上问题，现在提出一种共轭凸轮结合四连杆的组合打纬机构，筘座安装于连杆之上，共轭凸轮驱动四连杆，通过优化四连杆之间的几何关系，可以实现钢筘的水平打纬运动。图1 所示为共轭凸轮结合四连杆的组合打纬机构。

由图1 可知，该套机构由共轭凸轮、滚子、推杆、摆臂、连杆、钢筘及摇杆组成。电机通过减速器将驱动力传递给共轭凸轮，共轭凸轮绕回转轴O3做匀速转动，推程时主凸轮1 对滚子2 施加正压力，从而带动推杆3 与摆臂绕回转轴O1做顺时针摆动，此时连杆带动钢筘向前死心摆动；钢筘抵达前死心打纬结束后副凸轮1′对滚子2′施加正压力，从而驱动推杆3′与摆臂绕回转轴O1做逆时针摆动，钢筘与连杆一同向后死心位置摆动。之后滚子位于共轭凸轮休止圆部分，此时钢筘静止。根据引纬时间的长短，滚子位于共轭凸轮休止圆部分时可以控制电机减速或停转，来实现打纬与引纬的协调工作。通过对摆臂、连杆与摇杆的几何优化设计，可以实现钢筘在打纬前死心位置时处于竖直状态并做水平运动，即钢筘对每层纬纱的打纬力均匀。

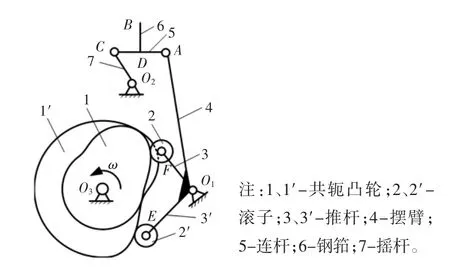
图1 共轭凸轮四连杆打纬机构Fig.1 Four-link weft beating-up mechanism of conjugate cam

2 组合打纬机构运动学设计

2.1 共轭凸轮廓线设计

建立xOy 直角坐标系，利用反转法求解共轭凸轮理论廓线，如图2 所示。

图2 共轭凸轮轮廓线反转法求解Fig.2 Outline inverse solution of conjugate cam

图2 中，直角坐标系以共轭凸轮基圆圆心为原点，摆杆转动中心与共轭凸轮基圆圆心中心距为a，摆杆长l，主摆杆位置初始角为ψ0，副摆杆位置初始角为ψ1，当共轭凸轮逆时针转过φ 后，摆动从动件相对于共轭凸轮顺时针转过φ 角，此时主副摆杆相对初始位置摆过ψ 角。

设主摆杆滚子回转中心坐标为（x1，y1），副摆杆滚子回转中心坐标为（x2，y2），则根据几何关系可得主凸轮理论廓线方程为：

副凸轮理论廓线方程为：

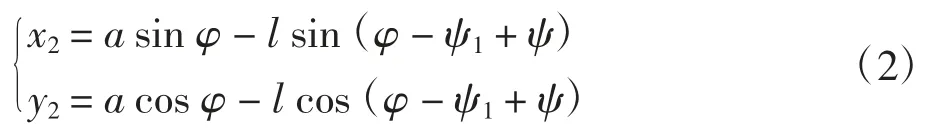
图 2 中点 G（xG，yG）是半径为 r 的滚子与主凸轮实际廓线的切点，则有滚子外圆方程：

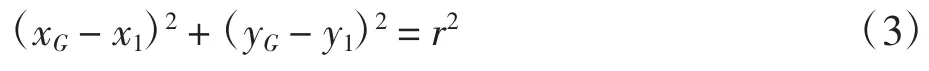
式（2）为关于φ 的函数，求偏导得：

联立式（2）、式（3）可得主凸轮实际廓线方程：

2.2 四连杆机构运动学分析

图3 为四连杆机构图。

图3 四连杆机构Fig.3 Mechanism of four-link

图3 建立直角坐标系，主副凸轮滚子推杆与摆臂l1固接，摆臂l1与连杆l2构成二级杆组，摆臂绕回转中心O1往复摆动，其与x 轴位置角为θ1，连杆l2在平面空间运动中与x 轴夹角为θ2。B 点为钢筘打纬受力点，运动中钢筘与连杆可看作同一构件，运动学分析时可将钢筘与连杆比作同一刚体。

向量 A、B、C 分别为点 A、B、C 的矢径，根据 RRR型二级杆组法[14]可知摆臂端点A 位移方程：

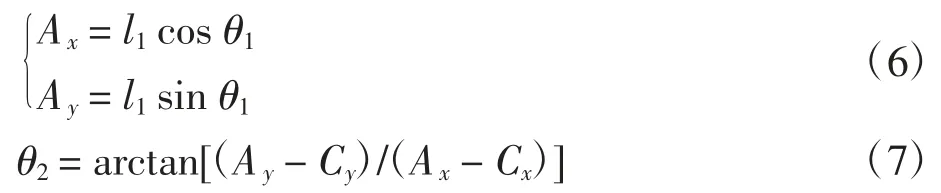
A 点与O1点为摆臂两端点，根据同一刚体上两点矢径关系可得：

式中：O1为摆臂端点O1的矢径。

式（8）减去式（9）可得：

整理得摆臂与连杆角速度：

将式（8）在直角坐标系两轴上分解得摆臂端点A速度分量：

对式（8）及式（9）分别关于时间求导得：

式（14）减式（15）得：

解得摆臂与连杆角加速度为：

式中：W=d2Cx/dt2-d2O1x/dt2+（dθ1/dt）2（Ax-O1x）-（dθ2/dt）2（Ax- Cx）；Q = d2Cy/dt2- d2O1y/dt2+（dθ1/dt）2（Ay-O1y）-（dθ2/dt）2（Ay-Cy）

将式（14）在直角坐标系两轴上分解得摆臂端点A加速度分量为：

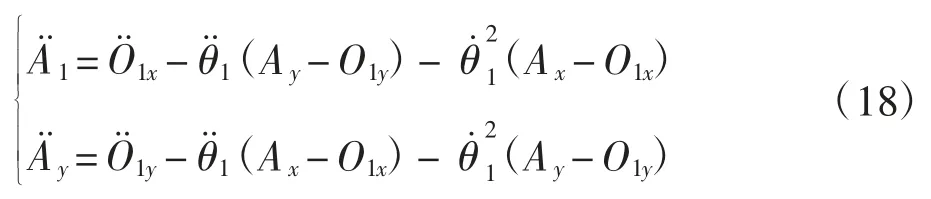
图3 中钢筘BD 与连杆AC 可看作同一刚体，根据刚体上任一点的运动分析[19]可知：

式中：A、B 分别为点 A 及点 B 的矢径，将式（19）对时间求导得：

将式（19）—式（21）分别在直角坐标系两轴上分解可得钢筘打纬阻力受力点B 位移、速度及加速度：

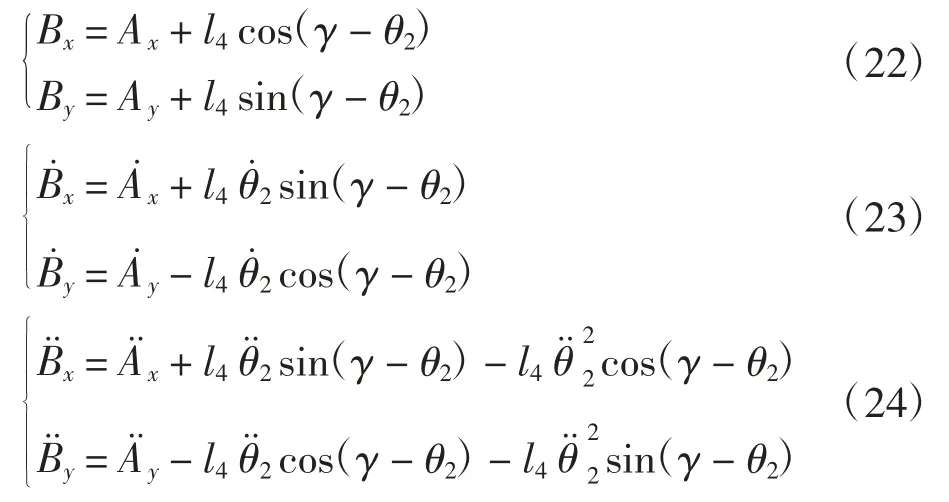
3 机构尺度优化

表1 示出组合打纬机构设计参数。

表1 组合打纬机构设计参数Tab.1 Design parameters of combined weft beating-up mechanism

根据表1 设计参数求得共轭凸轮轮廓线，在Adams 中进行运动仿真分析，给定共轭凸轮一定转速得出钢筘打纬受力点B 运动加速度及位移曲线，如图4 所示。

图4 钢筘水平位移及加速度Fig.4 Horizontal displacement and acceleration of reed

钢筘在前死心位置加速度负向最大，实现惯性打纬[20]。钢筘加速度由零开始到零结束且连续无突变，冲击小。

图5 为摆臂长与θ2关系。

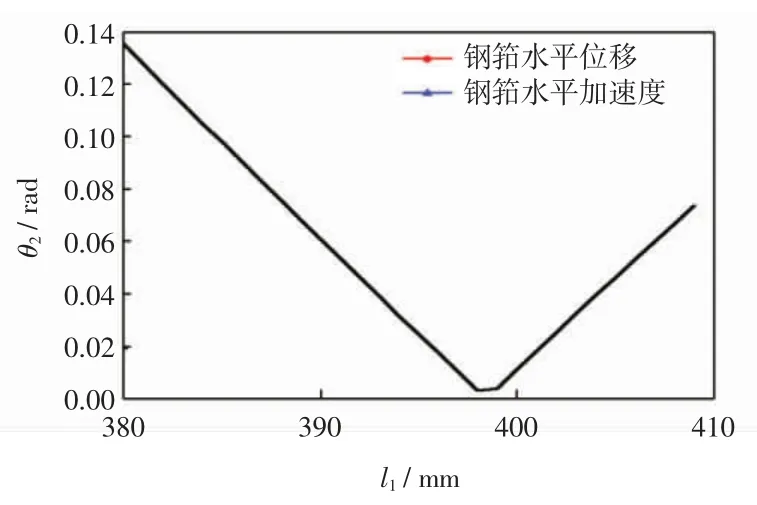
图5 摆臂长与θ2 关系Fig.5 Relationship between swinging arm and θ2

优化摆臂长可提高钢筘平行打纬性能，图5 中摆臂长取398 mm 时，打纬时刻钢筘运动方向与水平方向夹角θ2近似为0，即钢筘实现平行打纬。

钢筘满足平行打纬要求情况下，在其到达前死心位置时筘面与水平面垂直，如图3，筘面与水平轴相垂直时，摆臂l1也基本与水平轴线垂直，因此钢筘打纬动程与摆臂初始位置角θ1有关，摆臂初始位置角越小，则摆臂与水平轴相垂直所需的角位移越大，钢筘动程也越大。因碳纤维复合材料纱线摩擦易起毛特性，应在满足打纬工艺要求前提下尽量降低钢筘打纬动程，以减少钢筘对碳纤维复合材料纱线的摩擦，因此摆臂l1初始位置角θ1不宜过小，实际优化设计中其值取67.68°时满足小动程打纬，且满足引纬对钢筘与织口初始距离的要求。

钢筘是否实现平行打纬与四连杆杆长及铰支点分布有关，图3 坐标系下铰支点O2横纵坐标比例为19 ∶15 为宜。

图6 和图7 分别为优化连杆尺寸后钢筘位移和钢筘速度图。