基于虚拟元件的负载型四足步行平台静步态行走控制

2020-01-08谭永营晁智强金毅王飞

兵工学报 2019年12期

谭永营，晁智强，金毅，王飞

(1.陆军装甲兵学院车辆工程系，北京 100072；2.66336部队，河北保定 074000)

0 引言

负载型四足步行平台仅需地面一系列离散支撑点即可实现稳定行走，特殊的行走方式使其对复杂地形的适应能力强、对地面破坏作用小，在军用物资或装备运输、野外资源勘探等领域发挥着重要作用[1-3]。随着步行平台技术的发展，复杂环境中步行平台的行走控制成为研究热点。静步态是步行平台复杂环境中运用的主要步态之一[4-6]。在负载型四足步行平台静步态行走过程中，由于其机身质量较大、质心位置较高，常见的逆向运动学或动力学控制方法实时性差，易导致频繁的着地冲击，使机体不能较好地跟踪理想轨迹，满足其适应复杂地形的需求。因此，负载型四足步行平台静步态柔顺行走控制，对于保证其在复杂环境中的行走稳定性进而完成相应的任务具有重要作用。

Kolter等[7-8]和Kalakrishnanm等[9]在LittleDog整机动力学建模基础上，规划了LittleDog机体轨迹及足端摆动轨迹，运用阻抗控制方法对其静步态行走进行控制。但LittleDog动力学建模较复杂，控制效果的好坏取决于某些参数设置的准确性。Winker等借鉴了LittleDog静步态行走控制方法，将此种方法应用于液压四足步行平台(HyQ)静步态行走，实现了HyQ静步态行走控制，但建模准确性对平台静步态行走性能的影响极大，复杂的动力学计算也增加了控制器负担[10-11]。Wang等针对小型轮足式平台，选取机体高度、俯仰角、横滚角为主要控制自由度，运用虚拟悬挂模型及足端阻抗控制方式，实现了小型轮足式平台静步态行走[12]。LittleDog及HyQ中使用的静步态行走控制方法计算量较大，且需要对地形特征较为准确地建模，机身质量较大的负载型步行平台，建模过程中的误差将导致足端产生较大冲击，严重影响步行平台稳定性。对于选取主要控制自由度的方法，较大的机身质量将会放大任一自由度的问题，使平台无法保持稳定性。

虚拟元件控制方法计算过程简单、鲁棒性较好，已应用在仿人步行平台、四足步行平台对角步态和六足步行平台三角步态行走控制中[13-15]。本文为实现负载型四足步行平台静步态行走柔顺性，将虚拟元件引入平台行走控制中。在步行平台整体动力学建模基础上，将机体及摆动腿的运动控制需求转变为一系列虚拟力作用，运用二次规划方法实现平台虚拟力分配，并得到支撑腿及摆动腿的关节力矩。步行平台行走过程中能够感受地形的变化，进而实时调整各驱动关节力矩，实现复杂地形中的柔顺行走。

1 四足步行平台模型及其运动学分析

负载型四足步行平台模型如图1中所示，包括躯干和4条腿。每条腿均有3个自由度，从上到下依次为胯侧摆关节段、大腿和小腿，对应的关节分别为胯侧摆关节、胯纵摆关节和膝关节，且均为主动关节。为方便对步行平台机体及各腿段位姿的分析，在其机体质心处建立机体坐标系{Obxbybzb}，在各腿胯侧摆关节处建立各腿基坐标系{Oi0xi0yi0zi0}，i(i=1，2,3,4)为腿的编号，并选择大地上任一点建立绝对坐标系{Oxyz}，如图1所示。

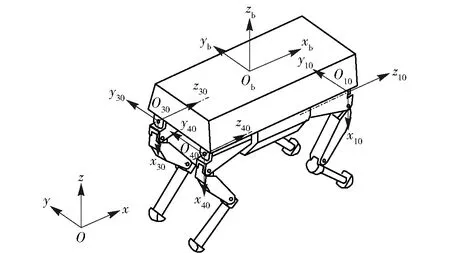
图1 步行平台模型及各坐标系Fig.1 Quadruped walking vehicle model and coordinates

各腿基坐标系x轴竖直向下，z轴与xb轴方向相同(见图1)。步行平台相关参数如表1所示。

表1 步行平台相关参数Tab.1 Relative parameters of quadruped walking vehicle

由于各腿结构相同且安装位置对称，仅对右前腿进行运动学分析，其余各腿运动学分析参考右前腿进行。运用Denavit-Hartenberg(D-H)方法对右前腿进行运动学分析，在各驱动关节及足端建立如图2所示坐标系，其中{O11x11y11z11}为胯侧摆关节坐标系，{O12x12y12z12}为胯纵摆关节坐标系，{O13x13y13z13}为膝关节坐标系，{O14x14y14z14}为足端坐标系。由旋转变换矩阵连乘可得1腿足端在其基坐标系中的坐标为

(1)

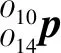
图2 D-H方法腿部坐标系Fig.2 Leg coordinates used in D-H calculating method

将(1)式对时间求导，可得步行平台足端点速度与关节角速度之间的关系[16]为

(2)

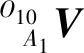
2 基于虚拟力优化分配的四足步行平台机体运动控制

虚拟元件控制方法是一种动力学近似的控制方法，其应用过程中忽略了各部分的加速度，不考虑惯性力的作用[17-19]。四足步行平台静步态行走过程中行走速度不高、加速度较小，且在步态规划时三足支撑阶段设计为匀速运动，四足支撑阶段存在较小的加速度，因此不考虑惯性力的方法是合理的。

2.1 四足步行平台整体动力学分析

假设四足步行平台的质量集中于机体的形心。四足步行平台静步态行走过程中，其所受合外力主要包括外界环境直接作用于步行平台机体的力、地面给足端的作用力、平台自身及负载质量的重力、空气阻力等。为方便对四足步行平台整体的动力学分析，根据平台静步态行走特点，可做出如下假设：

1)四足步行平台静步态行走过程中速度不高，可忽略空气对步行平台的阻力作用。

2)由于步行平台足端与地面接触面积较小，可将其看作点接触，只考虑足端与地面之间力的作用，而忽略力矩的作用。

3)假设外界环境对机体无直接干扰力。

4)步行平台静步态行走时，每次摆腿过程只有一条腿摆动，且腿的质量相对机体质量较小。因此不考虑腿的质量，且忽略摆腿对机体运动的影响。

四足步行平台静步态行走时的受力如图3和图4所示。图3中：Fx、Fy、Fz分别为沿xb轴、yb轴、zb轴的合外力；Tx、Ty、Tz分别为绕xb轴、yb轴、zb轴的合外力矩；fix、fiy、fiz分别为支撑腿足端沿xb轴、yb轴、zb轴方向的力，i=1，2，3，4；g为重力加速度。

图3 四足支撑受力Fig.3 Forces at four-leg supporting phase

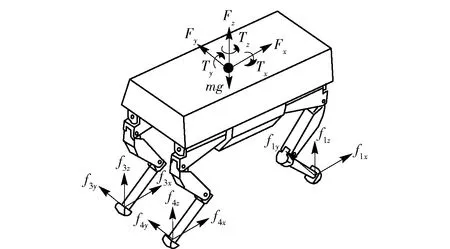
图4 三足支撑受力Fig.4 Forces at three-leg supporting phase

四足步行平台静步态行走过程中，需要控制支撑腿足端与地面之间的作用力，以保证其行走稳定性。因此，由图3和图4及相应的假设条件，可得步行平台受力方程为

(3)

式中：xi、yi、zi分别为i腿足端在xb轴、yb轴、zb轴方向的位置坐标；φy为机体俯仰角；n为支撑腿的数量。

2.2 四足步行平台机体虚拟元件的添加

在应用虚拟元件进行步行平台行走控制时，通常是在步行平台机体与参考坐标系或机体与步行平台某一部分之间添加虚拟元件，以实现平台期望的运动[20]。由四足步行平台绝对稳定裕度定义可知，其行走过程稳定性由机体质心在支撑平面的投影与足底支撑多边形的相对位置关系决定[4]。为保证步行平台行走过程中的稳定性，机体位置控制非常重要，而机体位置控制可通过控制作用于机体上的虚拟力实现。

为实现步行平台各自由度的运动可控，将机体控制任务分解到平台6个自由度上。在每个自由度的实际位置与期望位置间添加1维虚拟弹簧- 阻尼元件，以实现步行平台整体的期望运动，如图5所示。

图5 步行平台各自由度虚拟元件Fig.5 Vehicle’s virtual components for every degree of freedom

作用于质心上的合力及合力矩是由各自由度弹簧阻尼元件特性决定的。根据各自由度添加的一维虚拟弹簧- 阻尼元件模型，可得平台控制方程如下：

(4)

(5)

(6)

(7)

(8)

(9)

2.3 基于序列二次规划的虚拟力优化分配

在得到步行平台机体虚拟力后，将虚拟力分配到支撑腿足端，以实现步行平台行走控制。四足步行平台静步态行走占空系数大于等于0.75，在行走过程中存在三足支撑阶段和四足支撑阶段，两个阶段的虚拟力分配过程类似。参考文献[20-21]中的虚拟元件控制方法应用过程，针对多足步行平台虚拟力分配中的静不定问题，可通过添加约束矩阵或应用优化方法得到支撑腿足端的作用力。令四足步行平台机体所受合外力等于平台各自由度期望力，结合平台受力方程可得

(10)

四足步行平台静步态行走过程中足端与地面之间须保证稳定接触，防止因支撑腿打滑导致的稳定性问题。因此，足端力需满足如下摩擦圆锥约束条件：

(11)

式中：μi为足端所处地面的静摩擦系数。

在许多步行平台静步态行走研究中，为方便对支撑相的求解，往往假设足端与地面之间铰接，而实际上地面在竖直方向上只能产生支撑力、无法产生向下的拉力。因此

fiz≥0.

(12)

结合(8)式～(10)式可以发现，方程中共有3n(n=3或4)个未知量，但只有6个约束方程，其解有无限个。文献[22]利用序列二次规划方法对四足步行平台在陡坡间歇静步态行走过程中的足端力进行求解，实现了平台在高坡度地面的行走。下面参考文献[22]中的方法，并结合负载型四足步行平台协调静步态行走特点，对其足端力进行求解。

对(8)式进行整理，可得

Af=b，

(13)

式中：A为支撑矩阵；f为足端力列阵；b为期望合外力及力矩列阵。

(13)式中各矩阵的元素如下：

为使足端力满足上述约束条件，且足端力的绝对值能够尽量小，构建如下二次规划方程：

(14)

式中：fd为足端力期望值；S为虚拟力约束矩阵；α为权重系数；W为足端力惩罚矩阵；C为摩擦约束矩阵；D为足端力方向变换矩阵；fmin为足端力允许的最小值；fmax为足端力允许的最大值。

fmin与fmax根据步行平台行走过程中对足端力的期望值进行施加。α的值需恰当选择，防止两个约束条件相互干涉，出现稳定性问题，在此α取0.01.为简化足端力计算过程，以便使用序列二次规划方法进行求解，对足底摩擦圆锥进行线性化，采用棱锥代替摩擦圆锥。因此，(9)式变换为

(15)

(14)式中的约束矩阵C、D、fmin、fmax的计算公式分别如下：

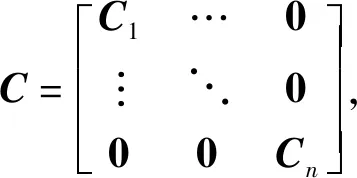
式中：θir为第i条腿足端所处地面倾角；fizmin为第i条腿足端垂向力的最小值，在此取200 N；fizmax为第i条腿足端垂向力的最大值，在此取∞.根据以上各式求解相应的二次规划，便可得到满足约束条件的足端力值。

2.4 四足步行平台支撑腿驱动关节力矩的求取

由虚拟力优化分配得到支撑腿足端的作用力后，由步行平台足端力与关节力矩之间的雅克比矩阵，可得各驱动关节力矩[17]如下：

(16)

在支撑腿足端力求解过程中考虑了足端打滑的条件，但求解过程中必须得到各足端所处地形的法线方向。虽然地形信息可以由步行平台搭载的地形感知系统得到，但也存在较大误差。因此，在各支撑腿足端实际位置与期望位置之间添加虚拟的低刚度弹簧元件，在保持机体稳定性的基础上，对各支撑腿垂直方向的足端力进行调整，以补偿地形感知过程中的误差。各支撑腿足端误差修正力可由(17)式求得：

(17)

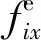
在得到水平方向的误差修正力后，利用试凑法对竖直方向的补偿力进行计算，以平台四足支撑为例：

Aefe=be，

(18)

式中：Ae为仅考虑垂直力的足端支撑矩阵；fe为支撑腿足端修正力列阵；be为期望的修正力列阵。(18)式中的矩阵元素如下：

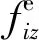
(19)

(20)

3 四足步行平台摆动腿运动控制

四足步行平台静步态行走过程中通过摆腿实现对障碍的跨越，仍以1腿为例对四足步行平台的摆腿进行说明。在1腿基坐标系的原点处建立如图6所示的坐标系{O10x1by1bz1b}，坐标系各轴平行于机体坐标系。将摆动腿的运动控制分解到沿坐标轴3个方向，在每个方向足端实际位置与理想位置之间添加虚拟的变刚度弹性阻尼元件，实现对摆动腿的控制。

图6 摆动腿虚拟元件控制Fig.6 Virtual model control of swing leg

为保证轨迹跟踪的准确性，在摆动段虚拟刚度较大而在落地段刚度减小，以实现足端的平稳着地。相应的控制方程如下：

(21)

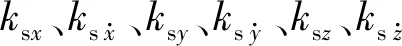
由摆动腿足端沿各坐标轴方向所受的力，结合摆动腿的雅克比矩阵，可得摆动腿各关节的力矩如下：

(22)

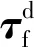
4 四足步行平台静步态行走状态机设计

四足步行平台静步态行走过程中，为满足迈腿过程中的稳定性要求，机体通常在前后方向和左右方向调整位置[23-25]。四足步行平台一个完整的步态周期如图7所示。由图7可见，步行平台静步态行走占空系数为5/6，每个步态周期存在4个三足支撑相(迈腿相)及2个四足支撑相(重心调整相)。理想情况下，迈3(4)腿及迈2(1)腿连续完成，中间不存在重心位置调整。图7所示为理想情况下四足步行平台静步态行走一个完整的步态周期。按照逆时针顺序将步行平台的腿编号为1、2、3、4，如图7(a)中所示。

图7 步行平台静步态行走示意图Fig.7 Locomotion strategy of static gait

四足步行平台复杂地形行走过程中，不可避免地要调整姿态，以充分利用足端活动空间、适应复杂地形。因此，在步行平台每次摆动腿着地时刻，判断地形变化是否超过设定的阈值。当地形变化超过设定阈值时，步行平台进入姿态调整相。假设φy0为步行平台初始姿态角，φys为感知到的地形坡度，φyc为设定的参考值。则当|φy0-φys|≤φyc时φyd=φy0，此时不调整姿态；当|φy0-φys|>φyc时φyd=φys，此时进行姿态调整。φys的计算公式如(23)式所示：

(23)

地形感知是在坐标系{Obxbwybwzbw}中进行的，如图8所示。

图8 步行平台地形感知Fig.8 Terrain sensing of walking vehicle

假设姿态调整时间为tc，为保证姿态角变化连续，采用5次曲线对其姿态变化过程进行规划如下：

(24)

由于负载型四足步行平台的机身质量较大，其姿态调整在四足支撑阶段完成，依靠各支撑腿与地面之间的相互作用力实现姿态的调整，而后进入正常的静步态行走周期。各相位的切换基于机体的姿态调整时间、摆动腿的摆腿时间、触地状态，最终得到其状态机如图9所示。

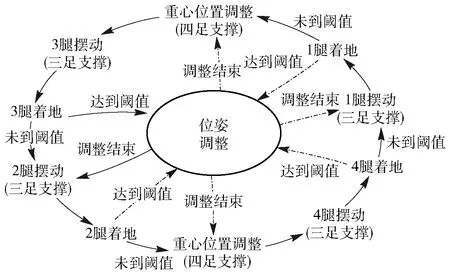
图9 状态机原理图Fig.9 Schematic diagram of state machine

5 四足步行平台静步态行走仿真实验

在ADAMS/View软件中建立四足步行平台的虚拟样机模型，在MATLAB/Simulink软件中编写相应的控制程序，实现步行平台静步态行走。在仿真过程中，MATLAB/Simulink软件计算得到的驱动关节力矩直接施加于步行平台的各驱动关节。为验证控制算法的有效性，分别对步行平台平地及复杂地形行走进行联合仿真。仿真过程中，步行平台的控制参数设置如表2所示。

四足步行平台平地行走过程中，迈腿时间Tsw及机体运动时间Tbm均为0.5 s.步行平台行走过程中机体轨迹跟踪误差、姿态角变化及1腿竖直方向的足端力变化如图10所示。

由图10(a)可见，步行平台前进方向及侧向的轨迹跟踪误差在0附近波动，且变化范围为-0.003～0.003 m，轨迹跟踪误差较小。着地冲击对轨迹跟踪几乎无影响。由图10(b)、图10(c)、图10(d)可见，步行平台平地行走过程中机体横滚角、俯仰角、偏航角均稳定在目标值0附近，且均在-0.001 5～0.001 5 rad范围内变化，步行平台机体稳定性较好。由图10(e)可见，平台摆动腿着地时刻仍然存在着地冲击力，冲击力的幅值约为900 N.与传统方法相比，足端着地力已大为减小，步行平台行走平稳。平地行走仿真结果表明，虚拟元件的控制方法较好地实现了负载型四足步行平台平地的静步态行走。

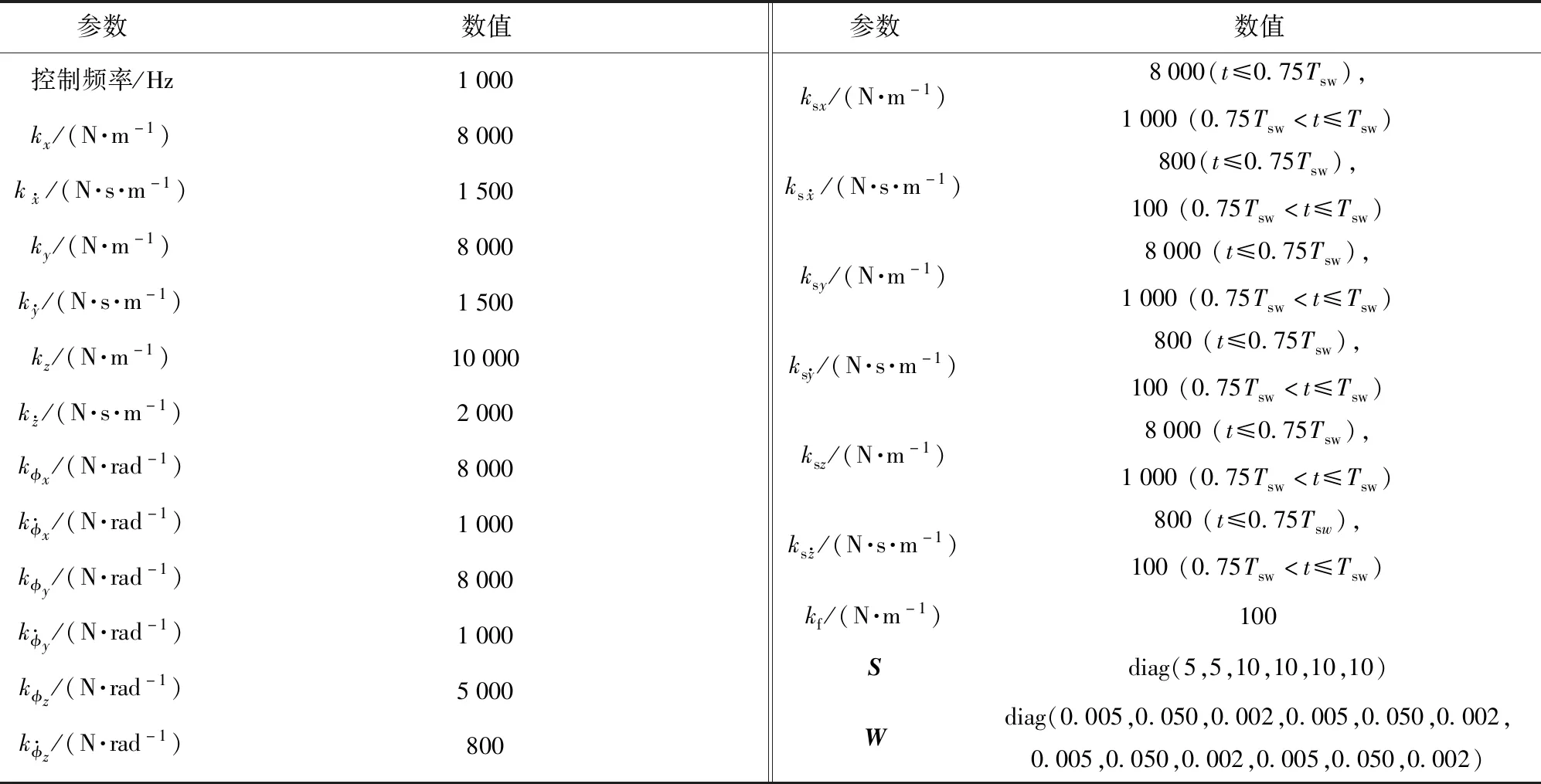
表2 仿真参数设置Tab.2 Simulation parameters setting

图10 步行平台平地行走参数变化Fig.10 Walking parameter change of vehicle on flat ground

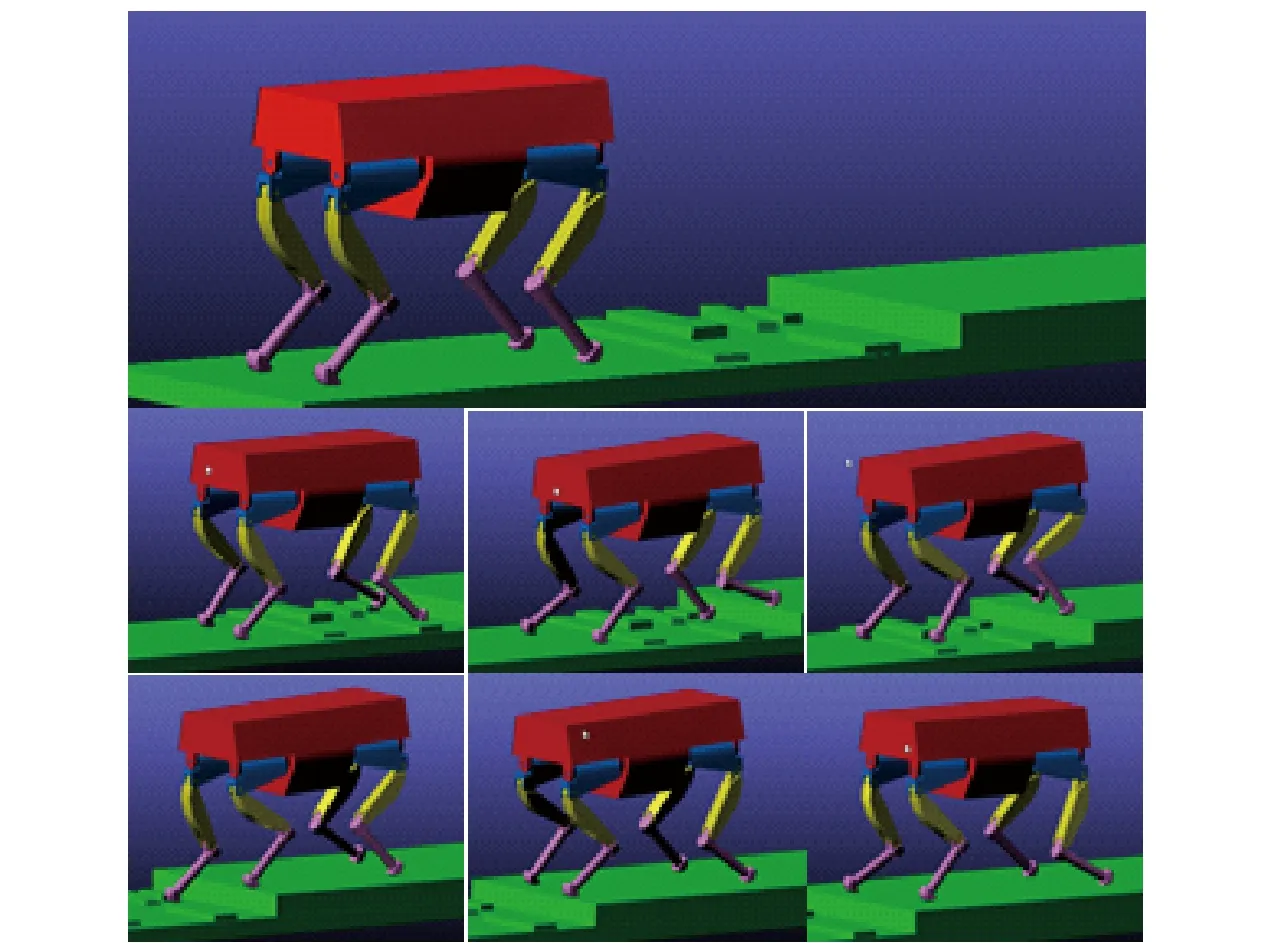
图11 仿真中构建的复杂地形及平台行走过程截图Fig.11 Rough terrain constructed in simulation and snapshots of vehicle while walking on rough terrain

为验证控制算法的鲁棒性，设计如图11所示的复杂地形，台阶高度为10 cm，其余障碍的高度在2～8 cm之间。步行平台行走过程中迈腿时间Tsw及机体运动时间Tbm均为1 s，且步行平台对复杂地形的信息未知。步行平台行走过程中机体姿态角及1腿竖直方向足端力的变化如图12所示。

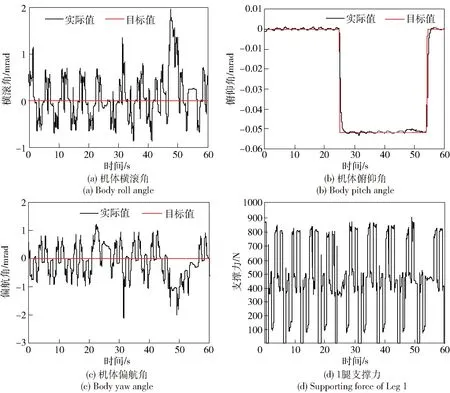
图12 步行平台复杂地形行走相关参数变化Fig.12 Walking parameter change of vehicle on rough terrain

由图12(a)、图12(c)可见，步行平台行走过程中机体横滚角、偏航角仍稳定在0附近，但由于障碍的影响变化范围有所增大，特别是在48 s左右，后腿与台阶之间的干涉导致机体横滚角、偏航角出现一定偏差，但各参数的变化均在可接受的范围内。在图12(b)中，静步态行走过程中步行平台根据地形特点计算得到俯仰角目标值，机体俯仰角实时跟随其目标值，以适应地形的变化。由图12中(d)可见，虽然行走过程中存在障碍，但足端冲击力仍然较小，步行平台平稳通过复杂地形。由步行平台复杂地形行走过程虚拟样机仿真可得，虚拟元件的控制方法实现了步行平台对复杂地形的适应性。