第Ⅱ重量级吊耳结构强度计算分析
2020-01-08谢子文林海彬朱照阳
付 凡 ,谢子文 ,林海彬 ,朱照阳
(1.空军装备部驻南昌地区军事代表室,江西 南昌,330024;2.航空工业洪都,江西 南昌,330024)
0 引言
机载悬挂结构一般采用滑块或吊耳连接,滑块结构一般用于小直径、轻质量机载悬挂物,而吊耳结构一般用于大直径、重质量机载悬挂物。随着飞机战术性能要求的不断提升,机载悬挂物向质量更重、体积更大、发射初速度更快的方向发展,机载悬挂物与吊挂装置连接部位、吊挂装置本身以及吊挂装置与飞机的连接部位的强度问题也凸显出来[1]。用于大直径、重质量机载悬挂物的吊耳结构是机载悬挂物上的关键部件,作为机载悬挂物与载机的连接接口,吊耳结构承受机载悬挂物在挂飞过程中各种工况下的极限载荷,对机载悬挂物与载机的安全性起至关重要的作用。
本文参考了GJB 1C-2006《机载悬挂物和悬挂装置结合部位的通用设计准则》[2]中规定的第Ⅱ重量级吊耳结构,建立三维数模和有限元模型,并在规定的载荷下对吊耳结构进行了强度校核,为机载吊耳结构的设计和生产提供了一定的理论依据。
1 吊耳结构模型
1.1 吊耳结构几何模型
GJB 1C中规定的第Ⅱ重量级吊耳结构二维数模如图1所示。
根据图1所示的吊耳二维数模,通过CATIA建立了吊耳结构的三维数模,如图2(a)所示。
1.2 吊耳结构有限元模型
GJB 1C中规定第Ⅱ重量级吊耳须承受180000N垂直方向的拉伸载荷,在垂直方向拉伸载荷作用下,吊耳结构的受力主要由最小截面A-A承受,理论上截取A-A截面以上部分模型建立有限元模型计算即可。为保证吊耳模型的完整性,对吊耳结构划分三部分网格,结构较为复杂的中间区域采用四面体网格过渡,其余部分以六面体网格为主建立了吊耳整体结构的有限元模型,如图 2(b)所示,共 13404个单元,10434个节点。
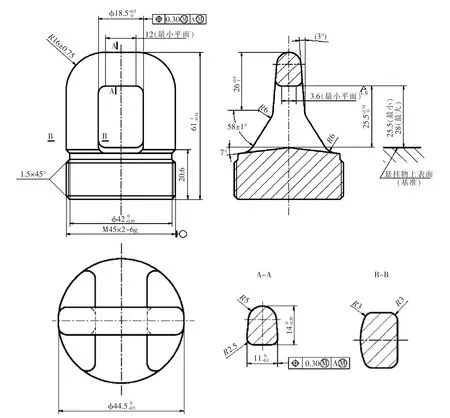
图1 第Ⅱ重量级悬挂物的355.6mm间距吊耳

图2 第Ⅱ重量级悬挂物的355.6mm间距吊耳
1.3 网格过渡性验证
由于吊耳结构有限元存在四面体与六面体网格的过渡,需验证四面体过渡网格对整体结构计算结果的影响。下面建立一简单算例验证四面体网格与六面体网格共节点后,模型传递力的特性。

图3 悬臂梁网格过渡模型
建立悬臂梁模型如图3所示,分别划分三种网格模型:全部为六面体网格的模型、中间有一段四面体网格的过渡模型、中间有两段四面体网格的过渡模型。梁的尺寸为20mm×20mm×200mm,梁材料弹性模量E=210000MPa,泊松比μ=0.3。模型一端固定,另一端分别施加法向垂直载荷和轴向拉伸载荷,从而计算不同模型变形与理论变形的误差影响。
首先对悬臂梁模型施加250N的垂直载荷,在垂直载荷作用下,悬臂梁的弯曲位移与应力结果如图4所示。
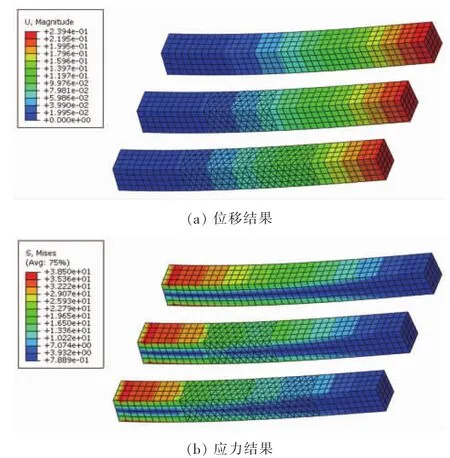
图4 垂直载荷作用下模型的位移和应力结果
垂直载荷作用下,悬臂梁位移的理论解为f=PL3/3EL=250×2003/(3×210000×(204/12))=0.238095mm
因此,弯曲位移有限元结果与理论解的对比如表1所示。

表1 弯曲位移有限元结果与理论解的对比
可以看出各模型位移结果相差不大,二段四面体模型与理论解的误差最大,为5.67%。
垂直载荷作用下,悬臂梁应力的理论解为

弯曲应力有限元结果与理论解的对比如表2所示。
可以看出,各模型应力结果一致,其与理论解的误差为2.67%,从而四面体网格对弯曲应力的影响很小。
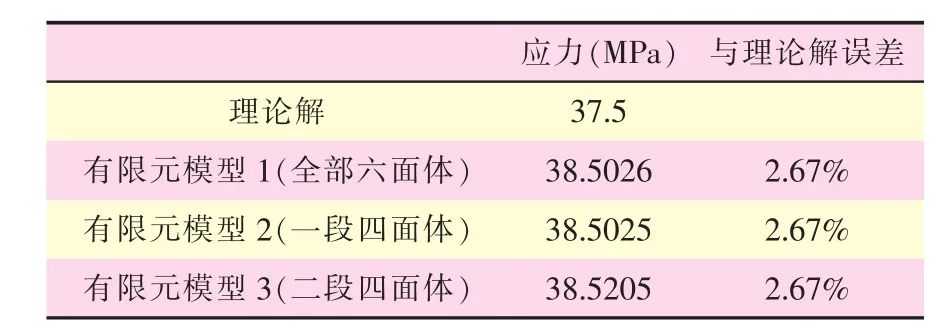
表2 弯曲应力有限元结果与理论解的对比
随后对悬臂梁模型施加25kN的轴向拉伸载荷,在拉伸载荷作用下,悬臂梁的拉伸位移和应力结果如图5所示。

图5 轴向拉伸载荷作用下位移结果与应力结果

因此,悬臂梁模型拉伸位移有限元结果与理论解的对比如表3所示。
悬臂梁轴向拉伸载荷作用下位移的理论解为
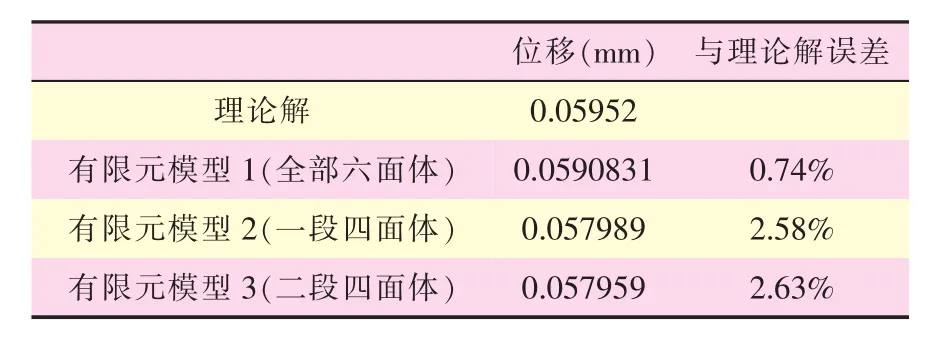
表3 悬臂梁模型拉伸位移有限元结果与理论解的对比
轴向拉伸载荷作用下各模型的位移结果与理论解相差很小,最大只有2.63%。
轴向载荷作用下,悬臂梁应力的理论解为
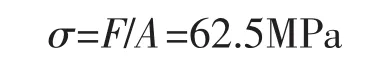
拉伸应力有限元结果与理论解的对比如表4所示。
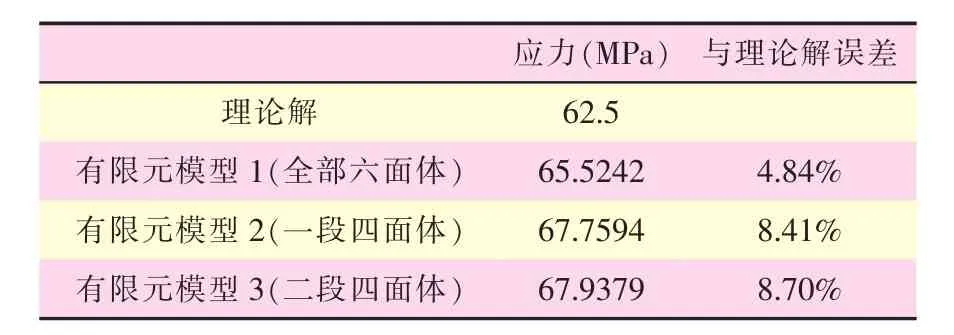
表4 悬臂梁模型拉伸应力有限元结果与理论解的对比
轴向拉伸载荷作用下各模型的应力结果与理论解的最大误差为8.70%。
从上面的悬臂梁算例可以看出,在弯矩载荷作用下,模型中四面体过渡网格对位移与应力结果影响都很小(最大为2.67%)。在轴向载荷作用下,四面体过渡网格对位移结果影响很小(最大2.63%),对应力结果稍有影响(最大8.70%),但仍在可接受范围内,从而可以认为,在模型中局部采用四面体网格过渡不影响整体模型受力的计算结果。
2 吊耳计算结果
GJB 1C中规定,第Ⅱ重量级吊耳须承受180000N垂直方向的拉伸载荷,但并没有规定吊耳采用哪种材料类型。因此在校核吊耳结构强度时需给定材料,30CrMnSiA[3]钢具有较高的强度、良好的韧性与淬透性,广泛应用于军工及民用工业,常用来制造承受巨大冲击及循环载荷的中等截面的重要零件,如飞机起落架、机翼主梁等,故指定吊耳结构材料采用30CrMnSiA钢,其弹性模量E=210GPa,泊松比μ=0.3,屈服强度为835MPa,强度极限为1080MPa。
2.1 考虑材料线弹性情况下的计算结果
首先将材料视为完全线弹性的情况,将吊耳底端固定,拉伸载荷施加在吊耳内侧,如图6所示。
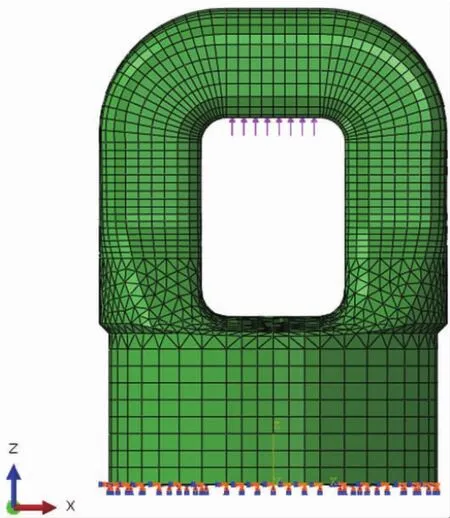
图6 吊耳加载和约束模型示意图
其计算结果如图7所示。
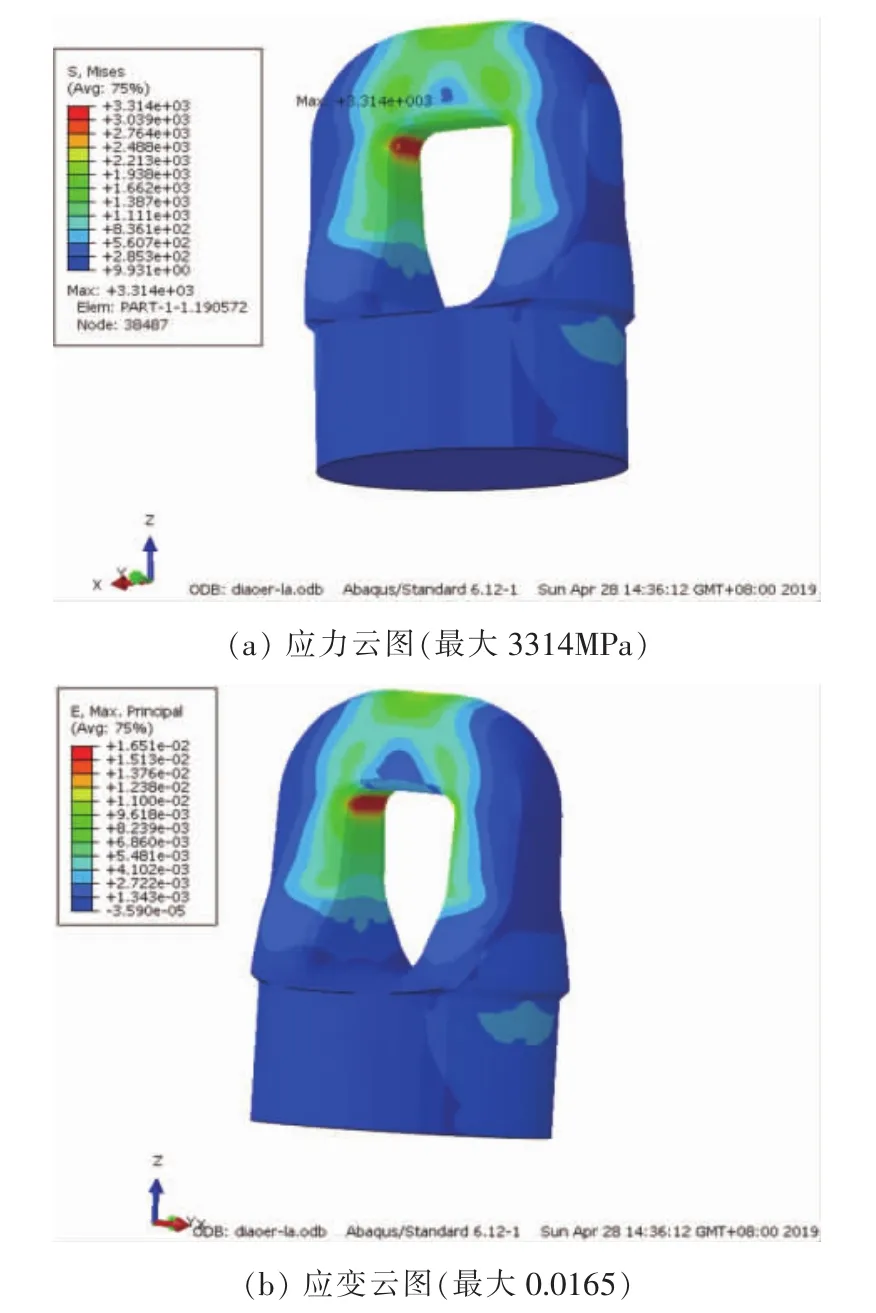
图7 吊耳应力云图(最大3314MPa)
从图7可以看出,材料完全线弹性情况下,吊耳的受力集中在耳孔内侧两端附近,最大应力为3314MPa,已经大大超出了材料的强度极限,不满足材料的使用要求,因此需考虑材料的塑性变形情况。
2.2 考虑材料塑性情况下的计算结果
考虑材料的塑性变形,其中30CrMnSiA的塑性变形参数如表5所示,采用同样的加载和约束方式,计算吊耳在180000N拉伸载荷作用下的变形情况。
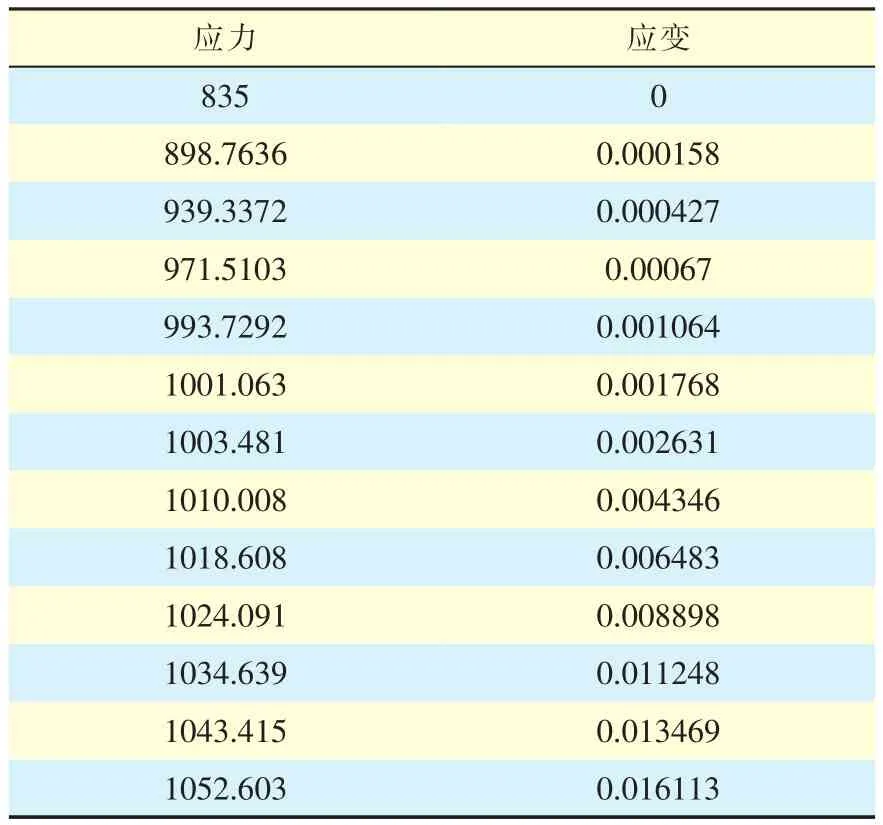
表5 30CrMnSiA的塑性变形参数
由于材料塑性的原因,在计算过程中,模型变形太大,应变甚至超过了1,结构位移也超过了10mm,这部分的计算结果在实际工程中并不会出现,已经没有参考意义。所以应舍弃这部分的计算结果,考虑到实际工程中结构的应变大多不超过0.02,故选取吊耳模型应变为0.02时的计算结果,此时应力、位移结果分别如图 8(a)、图 8(b)所示。

图8 应变为0.02时的应力云图和位移云图
从图中可以看出,此时吊耳结构的应力值最大为1129MPa,已经远超过了30CrMnSiA的屈服强度835MPa,略微超出极限强度1080MPa,从这个角度看,吊耳结构并不满足GJB 1C中规定的180000N的使用载荷。因此在使用吊耳结构时,需选用更高强度的钢材料替代30CrMnSiA钢。但更多的还是从工程实际出发,通过静力试验验证吊耳结构的强度。由于有限元计算结果显示模型局部应力过大,这可能是由于材料、加载方式等限制导致的,有必要利用工程算法计算吊耳结构的强度。
3 工程算法校核
吊耳承受拉伸载荷时,主要由其最小抗拉截面所承受,如图2(a)中的A-A截面所示,这与螺栓光杆承受拉力时的作用机理类似。飞机设计手册[4]中规定了材料为30CrMnSiA的螺栓破坏拉力,如表6所示。

表6 螺栓的破坏拉力(kN)
参考螺栓的破坏拉力,计算螺栓光杆承受破坏拉力时的应力值,如表7所示。
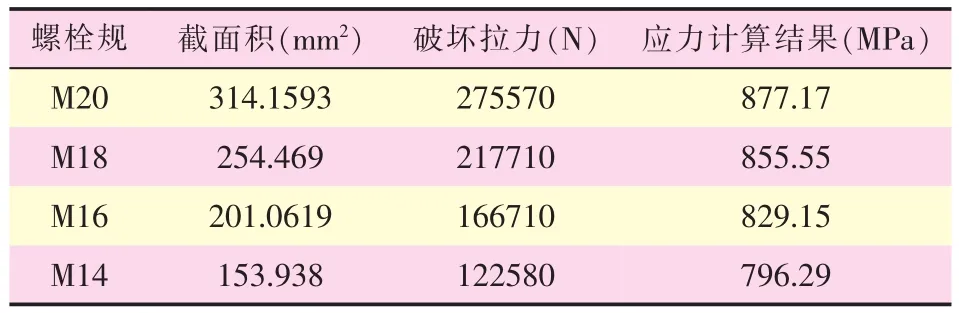
表7 30CrMnSiA螺栓光杆应力计算
此时若不考虑螺纹的影响,螺栓光杆在破坏拉力作用下的应力水平均低于材料的极限强度,而吊耳结构的最小抗拉截面的截面积为291mm2,介于M18与M20螺栓光杆截面积之间,故其理论破坏拉力载荷介于217710N与275570N之间,满足GJB 1C中规定的180000N的拉力载荷。
4 结论
本文针对GJB 1C-2006《机载悬挂物和悬挂装置结合部位的通用设计准则》中规定的第II重量级悬挂物的355.6mm间距吊耳结构,选取材料为30CrMnSiA,在规定的180000N拉力载荷作用下,建立四面体网格过渡模型进行强度计算,得到以下结论:
1)通过与理论解对比,四面体网格过渡模型对计算结果误差最大为8.7%,从而认为在模型中局部采用四面体网格过渡模型不影响整体模型受力的计算结果。
2)有限元计算结果显示,弹性情况下吊耳结构应力最大为3314MPa;塑性情况下,在应变为0.02时,结构最大应力为1129MPa,均超出材料强度极限,不满足材料使用要求。
3)在有限元结果不满足的情况下,进一步采用工程算法对吊耳结构进行校核,其理论破坏载荷介于217710N与275570N之间,符合GJB 1C中的要求。
