聚焦高考对概率统计大题考查的新视角

■安徽省宿州应用技术学校 张 刚

统计与概率知识在近几年高考全国Ⅰ卷考查中占有很重要的位置，由于它联系现实生活，注重数学应用，能很好地考查考生的数学核心素养。因此，概率与统计大题无疑是近几年高考数学考查的重点、热点内容，并且常考常新，每年都有精彩试题出现。下面以全国各地概率与统计部分模拟试题为例，聚焦概率与统计大题呈现的新视角，来帮助同学们更好地复习这部分内容。

视角1——古典概型与随机变量结缘

例1(2019年惠州高三第一次调研理20)甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司底薪70元，每单抽成2元；乙公司无底薪，40 单以内(含40 单)的部分每单抽成4元，超出40单的部分每单抽成6元。假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其100 天的送餐单数，得到表1 和表2所示的频数表：

表1 甲公司送餐员送餐单数频数表

表2 乙公司送餐员送餐单数频数表

(1)现从甲公司记录的这100 天中随机抽取2 天，求这2 天送餐单数都大于40 的概率。

(2)若将频率视为概率，回答以下问题：

①记乙公司送餐员日工资为X(单位：元)，求X 的分布列和数学期望；

②小明拟到甲、乙两家公司中的一家应聘送餐员，如果仅从日工资的角度考虑，请利用所学的统计学知识为他作出选择，并说明理由。

解析：(1)记“从甲公司抽取的2 天送餐单数都大于40”为事件M，则P(M)

(2)①设乙公司送餐员送餐单数为a。

当a=38时，X=38×4=152；

当a=39时，X=39×4=156；

当a=40时，X=40×4=160；

当a=41时，X=40×4+1×6=166；

当a=42时，X=40×4+2×6=172。

所以X 的所有可能取值为152，156，160，166，172。

所以X 的分布列如表3所示：

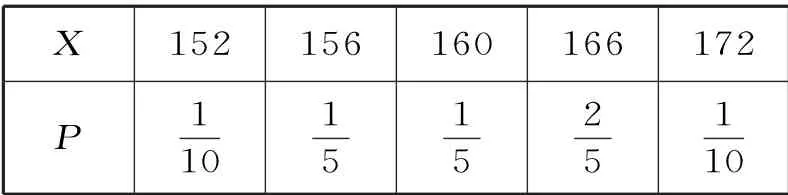
表3

②依题意，甲公司送餐员日平均送餐单数为38×0.2+39×0.4+40×0.2+41×0.1+42×0.1=39.5。

所以甲公司送餐员日平均工资为70+2×39.5=149(元)。

由①得乙公司送餐员日平均工资为162元。

因为149＜162，所以推荐小明去乙公司应聘。

点评：本题主要考查古典概型和随机变量的分布列，利用组合数法准确列举事件的种数，求出概率。根据离散型随机变量的分布列特征，求出数学期望，进行决策，从而解决实际生活问题，体现出高考对统计与概率这部分知识的综合应用的基础考查，一般这类题难度不大。

视角2——二项分布与茎叶图牵手

例2(2019年安徽高三上联考理20)前不久安徽省社科院发布了2017年度“安徽城市居民幸福排行榜”，铜陵市成为本年度安徽“最幸福城市”。随后师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度。现从调查人群中随机抽取16名，如图1 所示的茎叶图(以小数点前面的一位数字为茎，小数点后的一位数字为叶)记录了他们的幸福度分数。

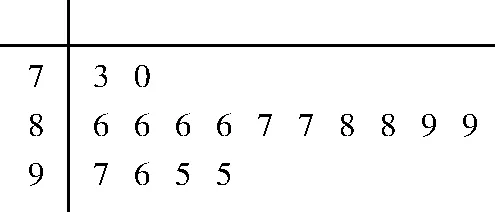
图1

(1)指出这组数据的众数和中位数；

(2)若幸福度不低于9.5分，则称该人的幸福度为“极幸福”，求从这16人中随机选取3 人，至多有1 人的幸福度是“极幸福”的概率；

(3)以这16人的样本数据估计整个社区的总体数据，若从该社区(人数很多)任选3人，记ξ 表示选到幸福度为“极幸福”的人数，求ξ 的分布列及数学期望。

解析：(1)由茎叶图知8.6出现的次数最多，所以众数为8.6；将茎叶图中的所有数据从小到大排列，得中位数为8.75。

(2)设事件Ai(i=0，1，2，3)表示所选3人中有i 人的幸福度是“极幸福”，至多有1人的幸福度是“极幸福”记为事件A，结合茎叶图得P(A)=P(A0)+P(A1)

(3)方法一：ξ 的所有可能取值为0，1，2，3，由样本估计总体知，任选1人，其幸福度为“极幸福”的概率为，则P(ξ=0)=

所以ξ 的分布列如表4所示：

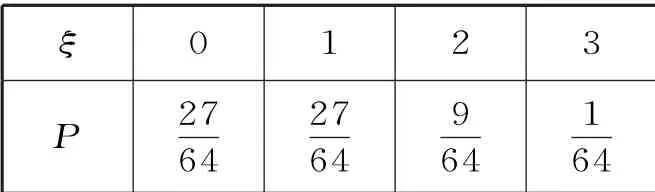
表4

方法二：ξ 的所有可能取值为0，1，2，3，由样本估计总体知，任选1 人，其幸福度为“极幸福”的概率为

所以ξ 的分布列如表5所示：

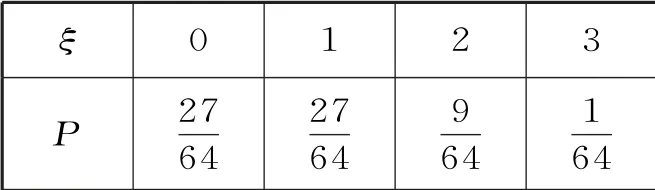
表5

点评：若有n 个相互独立的事件，每个事件在一次实验中发生的概率均为P，设在一次实验中这n 个相互独立事件发生的个数为随机变量ξ，则ξ服从二项分布，即ξ～B(n，p)。

视角3——正态分布与概率统计交汇

例3(2019年安徽五校联盟高三上第二次质检理20)在某市高中某学科竞赛中，某一个区4 000名考生中的参赛成绩统计图如图2所示。

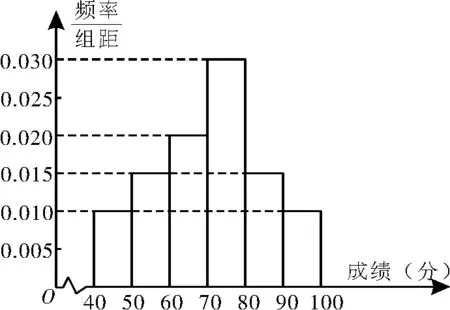
图2

(2)由直方图可认为考生竞赛成绩z 服从正态分布，N(μ，σ2)，其中μ，σ2分别取考生的平均成绩和考生成绩的方差s2，那么该区4 000 名考生的成绩超过84.81 分(含84.81分)的人数估计有多少?

(3)如果用该区参赛考生成绩的情况来估计全市的参赛考生的成绩情况，现从全市参赛考生中随机抽取4 名，记成绩不超过84.81分的考生人数为ξ，求P(ξ≤3)。(精确到0.001)

附：①s2=204.75，≈14.31；②0.841 34≈0.501；③z～N(μ，σ2)，则P(μ-σ＜z＜μ+σ)≈0.682 7，P(μ-2σ＜z＜μ+2σ)≈0.954 5。

解析：(1)由题意可得表6。

表6

(2)依题意z 服从正态分布N(μ，σ2)，其中μ==70.5，σ2=D(ξ)=204.75，σ=14.31，所以z服从正态分布N (μ，σ2)=N(70.5，14.312)。

而P(μ-σ＜z＜μ+σ)=P(56.19＜z＜84.81)≈0.682 7，所以P(z≥84.81)≈≈0.158 7。

又0.158 7×4 000=634.8≈635，所以竞赛成绩超过84.81分的人数估计为635。

(3)全市竞赛考生的成绩不超过84.81分的概率P ≈1-0.158 7=0.841 3。

因为ξ～B(4，0.841 3)，所以P(ξ≤3)=1-P(ξ=4)=1-×0.841 34≈1-0.501=0.499。

点评：平均值要用每组区间中点值乘以该组的频率，然后求和得到。关于人数估计，可以利用正态分布曲线的对称性求解，本题易知成绩不超过84.81分的考生人数ξ 服从二项分布，进而可以求解。

视角4——独立性检验与2×2 列联表交叉

例4(2019年洛阳高三第二次统考理20)某共享单车经营企业欲向甲市投放单车，为制定适宜的经营策略，该企业首先在已投放单车的乙市进行单车使用情况调查。调查过程分随机问卷、整理分析及开座谈会三个阶段，在随机问卷阶段，A，B 两个调查小组分赴全市不同区域发放问卷并及时收回；在整理分析阶段，两个调查小组从所获取的有效问卷中，针对15至45岁的人群，按比例随机抽取了300份，进行数据统计，具体情况如表7所示：

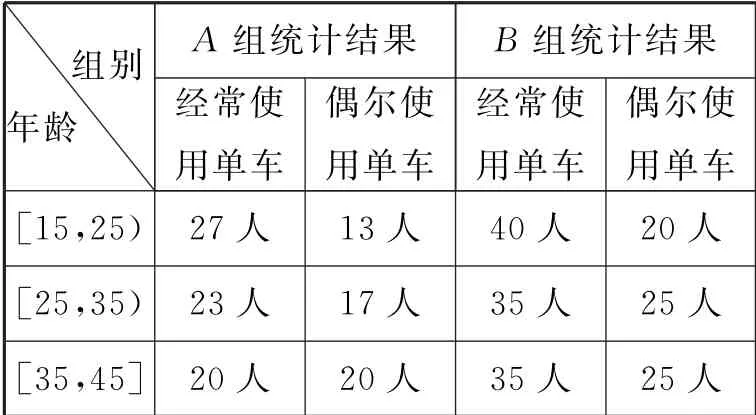
表7

(1)先用分层抽样的方法从上述300 人中按“年龄是否达到35 岁”抽出一个容量为60人的样本，再用分层抽样的方法将“年龄达到35岁”的被抽个体分配到“经常使用单车”和“偶尔使用单车”中去。

①求这60人中“年龄达到35 岁且偶尔使用单车”的人数。

②为听取对发展共享单车的建议，调查小组专门组织所抽取的“年龄达到35岁且偶尔使用单车”的人员召开座谈会。会后共有3份礼品赠送给其中3人，每人1份(其余人员仅赠送骑行优惠券)。已知参加座谈会的人员中有且只有4人来自A 组，求A 组这4人中得到礼品的人数X 的分布列和数学期望。

(2)从统计数据可直观得出“经常使用共享单车与年龄达到m 岁有关”的结论。在用独立性检验的方法说明该结论成立时，为使犯错误的概率尽可能小，年龄m 应取25 还是35? 请通过比较K2的观测值的大小加以说明。

解析：(1)①从300人中抽取60人，其中“年龄达到35 岁”的人数为再将这20人用分层抽样法按“是否经常使用单车”进行名额划分，其中“年龄达到35岁且偶尔使用单车”的人数为

②A 组这4人中得到礼品的人数X 的所有可能取值为0，1，2，3，相应概率为P(X=0)

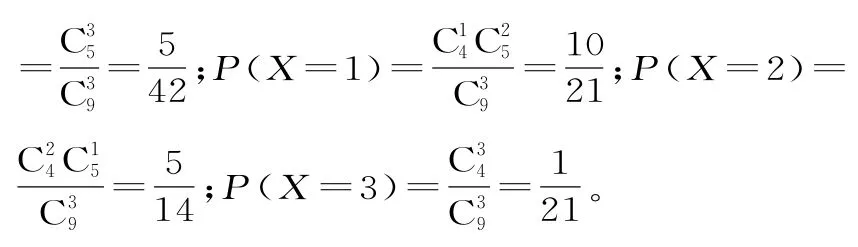
故X 的分布列为表8：

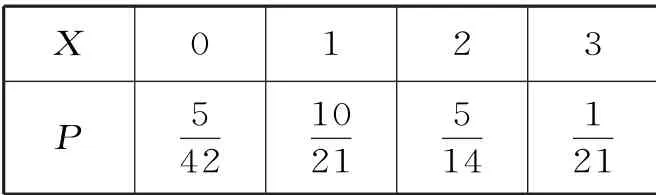
表8

(2)按“年龄是否达到35岁”对数据进行整理，得到如表9所示的列联表：

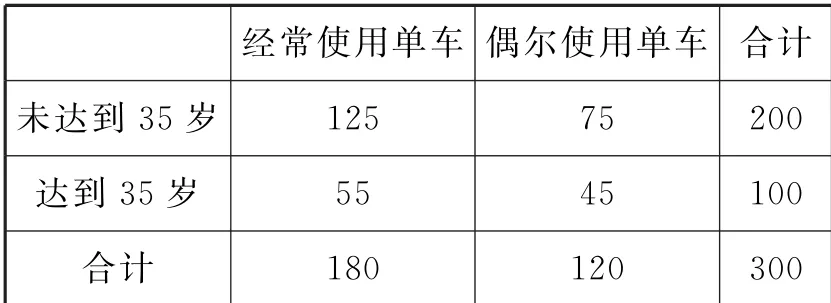
表9

当m=35(岁)时，可求得K2的观测值：

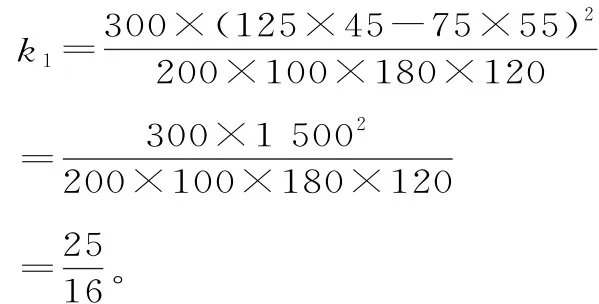
按“年龄是否达到25 岁”对数据进行整理，得到如表10所示的列联表：

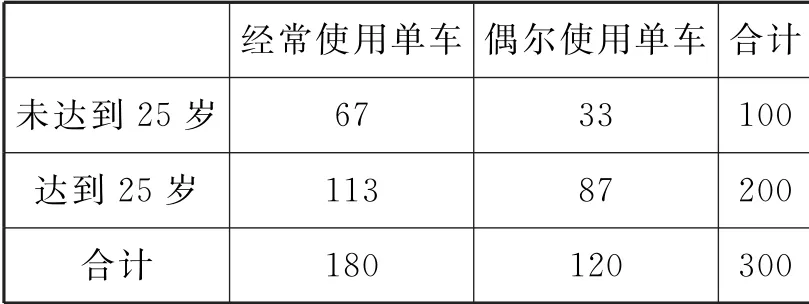
表10

当m=25(岁)时，可求得K2的观测值：

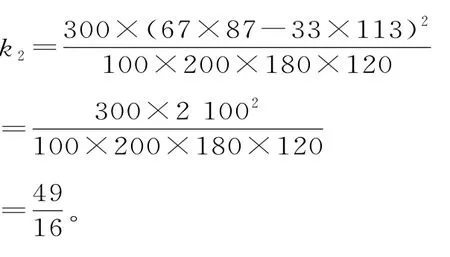
所以k2＞k1。

欲使犯错误的概率尽可能小，年龄应取m=25。

点评：本题主要考查独立性检验与2×2列联表的计算公式的运用。正确读懂“年龄是否达到35岁”与“年龄是否达到25岁”，从而建立2×2列联表计算观测值k1，k2是关键，比较大小即可得出m 的值。其中使用公式解题时的运算能力是准确求解的关键，近年来的高考题，统计内容通常都与概率知识结合在一起考查，体现出高考在知识交汇处命题的原则。

通过对以上高考模拟试题中出现的概率与统计大题的赏析，我们发现，高考中的这类概率与统计大题具有一定的灵活性、应用性、交汇性，特别是今年全国Ⅰ卷甚至出现在压轴题的位置。因此，同学们要引起足够的重视，加强语言文字的阅读能力，提高概率统计知识与其他知识的融合能力。只要我们立足基础，掌握基本方法，跟踪把握高考命题规律，就能做到心中有数，触类旁通。