鉴古知今,追本溯源
———探索简易逻辑母源题
2020-01-06江苏省宿豫中学
■江苏省宿豫中学 孙 艳
正确的思想一定是来自于正确的逻辑,能够清晰高效地思考,能与人顺畅地沟通,逻辑学的功劳不可磨灭。逻辑之艺术非天外来客,它是人们生活中行动与思考的核心所在。数学就是逻辑的代名词,而中学时代的简易逻辑是逻辑最初的模样。在高考的舞台上,简易逻辑也有一席之地,虽然考试难度并不大,但是给予一定的关注是非常有必要的。
简易逻辑的高考命题每年都有新变化,但若认真研究就会发现还是有规律可循。正所谓万变不离其宗,可以说高考考题都是可以找见它的母源题的。若是掌握这些母源题,无论高考考题如何变化,都可以以不变应万变,在高考中创造出辉煌的成绩。
【母源题一】(人教A 版选修1-1第11页例3)下列各题中,哪些p 是q 的充要条件?
(1)p:b=0;q:函数f(x)=ax2+bx+c是偶函数。
(2)p:x>0,y>0;q:xy>0。
(3)p:a>b;q:a+c>b+c。
【创新应用1】已知命题p:“关于x 的方程x2-4x+a=0有实根”,若¬p 为真命题的充分不必要条件为a>3m+1,则实数m的取值范围是( )。
A.(1,+∞) B.[1,+∞)
C.(-∞,1) D.(-∞,1]
解析:对于命题p:方程x2-4x+a=0有实根,得Δ=16-4a≥0,则a≤4,所以¬p成立时a>4。又a>3m+1是¬p 为真命题的充分不必要条件,所以3m+1>4,m >1,即实数m 的取值范围是(1,+∞)。
【创新应用2】设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0。若¬p是¬q 的必要不充分条件,则实数a 的取值范围是____。
解析:设A={x|(4x-3)2≤1},B=¬p 是¬q 的必要不充分条件,可知p 是q的充分不必要条件,则A 是B 的真子集,所以即故实数a 的取值范围是
评注:该类试题在考查题型上,通常以选择题或填空题的形式出现,难度较小,往往与命题(特别是含有逻辑联结词的复合命题)真假的判断、充分条件与必要条件的判断,以及全称命题、特称命题等联系紧密。
充分、必要条件的三种判断方法:
(1)定义法。直接判断“若p,则q”、“若q,则p”的真假。例如“p⇒q”为真,则p 是q的充分条件。
(2)等价法。利用p⇒q 与¬q⇒¬p,q⇔p 与¬p⇒¬q,p⇔q 与¬q⇔¬p 的等价关系,对于条件或结论是否定式的命题,一般运用等价法。
(3)集合法。若A ⊆B,则A 是B 的充分条件或B 是A 的必要条件;若B⊆A,则A是B 的必要条件;若A=B,则A 是B 的充要条件;若A 是B 的真子集,则A 是B 的充分不必要条件;若B 是A 的真子集,则A 是B 的必要不充分条件。
【母源题二】(人教A 版选修1-1第23页例2(节选))判断下列特称命题的真假:
解析:因为命题“∃x0∈R,-2x+m≤0”是假命题,所以∀x∈R,x2-2x+m>0为真命题,根据一元二次不等式解的讨论,可知Δ=4-4m <0,解得m >1,故答案为(1,+∞)。
评注:解决与简易逻辑问题有关的参数问题,需要明确逻辑联接词的含义,以及全称量词、特称量词包含的数学理论。
【母源题三】(人教A 版选修1-1第17页例4)写出下列命题的否定,并判断它们的真假:
(1)p:y=sin x 是周期函数;
(2)p:3<2;
(3)p:空集是集合A 的子集。
【创新应用4】(2019 年高考全国Ⅲ卷文11题)记不等式组表示的平面区域为D。命题p:∃(x,y)∈D,2x+y≥9;命题q:∀(x,y)∈D,2x+y≤12。下面给出了四个命题:①p∨q;②¬p∨q;③p∧¬q;④¬p∧¬q。在这四个命题中,所有真命题的编号是( )。
A.①③ B.①②
C.②③ D.③④
解析:根据题中的不等式组,可作出可行域,如图1 中阴影部分所示。记直线l1:y=-2x+9,l2:y=-2x+12,由图可知,∃(x,y)∈D,2x+y≥9,∃(x,y)∈D,2x+y>12,所以p 为真命题,q 为 假 命 题,则¬p 为假命题,¬q 为真命题,从而p∨q 为真命题,¬p∨q为假命题,p∧¬q 为真命题,¬p∧¬q 为假命题,则所有真命题的编号是①③。故选A。
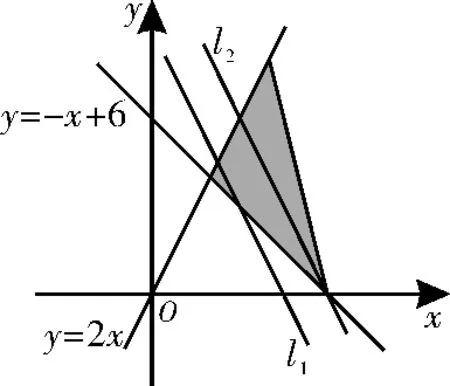
图1
评注:本题将线性规划、不等式与命题判断综合到一起,解题关键在于充分利用数形结合法进行判断命题真假。进而通过命题p、命题q 的真假,确定命题p∨q,p∧q,¬p的真假。命题p∨q,p∧q,¬p 的真假判断如表1:
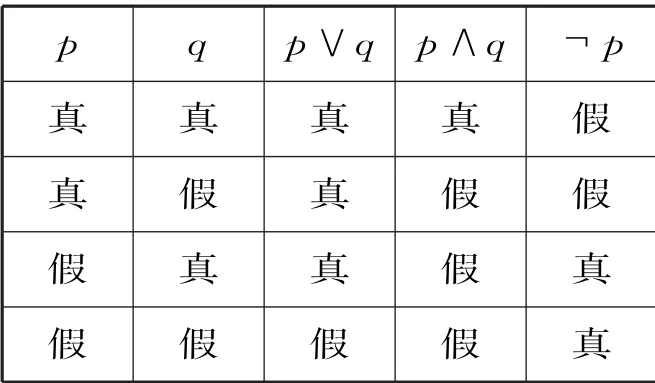
表1
【母源题四】(人教A 版选修1-1第7页探究(节选))以“若x2-3x+2=0,则x=2”为原命题,写出它的逆命题、否命题与逆否命题,并判断这些命题的真假。
【创新应用5】命题:“已知实数a,b,若|a|+|b|=0,则a=b。”则该命题的否命题是____,命题的否定是____。
解析:根据否命题与命题的否定的意义可知,否命题为:“已知实数a,b,若|a|+|b|≠0,则a≠b”;命题的否定为:“已知实数a,b,若|a|+|b|=0,则a≠b”。
评注:命题的否定和否命题是两个容易混淆的概念,前者只否定结论,后者的条件和结论都要进行否定。特别地,在否定条件或结论时,应把“且”改成“或”、“或”改成“且”。
有关简易逻辑的母源题就探寻到这里,文虽至此,但是研究的脚步不会停止。因为有这么一种现象总是让人非常揪心,在高中学生中常看到一些平时非常用功,但是学习成绩不太好的学生。若用心研究这类学生,不难发现他们具有相同的特点,就是大多数都不知道自己的薄弱点,虽然有大量的练习,然而并没有针对自己的薄弱之处练习,大量的精力花在不需要的地方。这就如同老师在网络上下载了大量电子版本的资料,却因为精品不多,导致题目是越来越多,反而成为一种负担,这样既苦了自己,也苦了学生。
为了化解上述难题,对学生而言,需要明确目标,进行有针对性的练习,才能提高复习质量。这就需要有人帮助学生找到他们知识体系中的不足,引导他们将精力投入到学习薄弱的环节,所以探索出数学“母源题”,并利用“母源题”搞好数学复习工作。这样可以避免无的放矢、机械训练、重复操练,从而跳出“题海”。
