射流泵装置性能预测方法
2020-01-03邹晨海李红向清江汤攀陈超
邹晨海, 李红, 向清江, 汤攀, 陈超
(江苏大学国家水泵及系统工程技术研究中心, 江苏 镇江 212013)
由于中西部地区地表及地下水位不断下降,许多灌排地区水位距地面8 m以上.由于离心泵结构原理所限,普通离心泵的吸上高度在5 m以下,不能满足该地区的提水灌溉要求[1].常用的提水装备例如潜水电泵、长轴深井泵等,都由电动机驱动,在中西部很多无电网或缺电地区无法使用.而射流泵装置由离心泵和射流泵组成,吸上高度可达10 m,有的可达20 m以上,并且可用汽、柴油机驱动[2-3].
在射流泵装置开发过程中,若搭建试验台直接测量射流泵装置在实际吸上高度时的性能,则成本高、耗时久.目前缺乏专门针对超高吸程水泵的性能检测试验台,装置出厂前也无法进行实际吸程的高吸程试验,影响了装置的设计效率和可靠性.因此,建立较准确的射流泵装置性能预测公式,可以极大地减少装置的试验环节,减少开发周期和成本.陆宏圻等[4]和龙新平等[5]提出了比较具体的射流泵装置的设计方法,并采用数值解法通过装置性能方程预测装置性能.龙新平等[6]根据射流泵装置串并联的特殊形式将射流泵中的离心泵看作同时向高低水池供水,采用图解法通过装置特性曲线与离心泵性能曲线的交点确定工作点处装置性能.然而,这2种预测方法均利用射流泵基本方程作为预测依据,由于基本方程为简化方程,忽略了除面积比以外的所有尺寸参数,因而对最后整个装置的预测精度产生较大影响,且作图法中未考虑出水口部件(阀门、喷头等)局部阻力损失的影响.此外,已有研究结果未根据试验数据对预测结果进行修正,对装置性能的预测结果仍存在较大的误差.
为了建立较准确的射流泵装置性能预测方法,文中采用射流泵性能试验结果作为初始条件,通过不同吸上高度时得到的预测结果与实际吸上高度性能试验结果的误差分析,选用误差较小的预测方法进行修正.引入射流泵扬程Hc的修正值与预测值之比(修正系数α),采用Plackett-Burman试验设计[7]筛选出对Hc影响最大的参数,选择拟合优度最高的拟合公式作为修正系数α的计算公式并进行试验验证,建立射流泵装置性能预测方法.
1 射流泵装置性能预测方法
1.1 射流泵装置结构及水力参数
射流泵装置由射流泵、离心泵及管路系统组成,如图1所示.

图1 射流泵装置吸程试验台示意图
Fig.1 Schematic of test rig for jet pump installation with suction height
射流泵装置的工作原理:工作液体经过离心泵加压后,由进水管经过射流泵喷嘴进入射流泵,通过射流介质的卷吸效应和紊动扩散作用,在射流泵喉管入口处形成负压,被吸液体在大气压力作用下被抽吸进入喉管与工作液体混合进行能量交换,被吸液体得到动能与工作液体一起通过回水管回到离心泵,使吸上高度达到10 m以上.
射流泵由喷嘴、吸入室、喉管和扩散管4部分组成,如图2所示,图中D,d分别为喉管截面直径、喷嘴出口截面直径.射流泵依靠一定压力的工作流体通过喷嘴高速喷出带走被输送流体.

图2 射流泵结构示意图
射流泵的主要参数包括面积比m、流量比q和压力比h等,用下列量纲一的量表示.
1) 射流泵面积比为
(1)
式中:F2为喉管截面积,m2;F1为喷嘴出口截面积,m2.
由于喉管和喷嘴出口都为圆形截面,故面积比也可表示为喉管截面直径D的平方与喷嘴出口截面直径d的平方之比.
2) 射流泵流量比为
(2)
式中:Qs为被吸液流量,m3/h;Q0为工作液流量,m3/h.
3) 射流泵压力比(扬程比)为
(3)
式中:Δpc为射流泵出口压力,Pa;Δp0为射流泵进口压力,Pa;Hc为射流泵扬程,m;Hs为射流泵吸程,m;H1为工作液扬程,m.
射流泵扬程Hc是直接反映射流泵装置吸上能力的重要性能参数.
射流泵装置的性能预测方法主要有数值解法和特性曲线图解法.确定射流泵与离心泵的性能曲线方程为2种预测方法的前提,一般采用射流泵基本方程得到射流泵性能曲线.为了减小预测误差,采用性能试验得到射流泵和离心泵的性能曲线并作为初始条件.
1.2 数值解法
数值解法是将射流泵装置看成整体,代入射流泵装置性能方程,通过计算装置性能系数S预测各工况点性能参数.具体步骤如下.
1) 推导离心泵流量.将射流泵装置看作整体,引入装置性能系数S,射流泵装置的性能方程为
Hp=SQ2,
(4)
式中:Hp为离心泵扬程;Q为离心泵流量,即装置流量.
射流泵装置总扬程即为离心泵扬程,装置性能也可表达为
Hp=AQ2+BQ+C,
(5)
式中:A,B,C为离心泵性能方程常数.
联立装置性能方程(1)和(2),约去H后可解得:
(6)
2) 确定射流泵装置性能系数S.根据射流泵装置各个断面的能量关系,可以求得装置性能系数S表达式为
(7)
式中:K2=(μ1f1)2/2gα2;μ1为射流泵喷嘴流量系数;f1为喷嘴出口断面面积,m2;Sb,Sc分别为进、出水管阻力系数.
3) 计算射流泵扬程.根据压力比h定义式,求得射流泵扬程为
Hc=(ΔHp-ΔHs+ΔH-hb)h,
(8)
式中:H为吸上高度,m;hb为进水管阻力损失水头,m.
将离心泵流量Q代入式(5)求得离心泵扬程Hp.
根据以上计算步骤,得到射流泵装置在吸上高度为4.5和9.0 m时各工况点的预测结果,如表1所示.
表1 不同吸上高度时各工况点的数值解法预测结果
Tab.1 Heads predicted by analytic method at different suction heights

H/mqhHc/mQ/(m3·h-1)Hp/m4.50.10.2515.1617.1556.080.30.2012.0617.8555.960.50.169.5818.2355.890.70.158.9919.0655.730.90.137.8020.1455.509.00.10.2516.4712.9656.580.30.2013.3213.8556.500.50.1610.5618.1155.910.70.159.9111.8756.660.90.138.4219.9555.54
1.3 特性曲线图解法
如图3所示(图中R1为压力管路特性曲线,R2为出水管路特性曲线,R3为装置特性曲线,R′2为加入阀门局部阻力损失后的出水管路特性曲线,R′3为加入阀门局部阻力损失后的装置特性曲线),特性曲线图解法是将射流泵装置中的离心泵看成同时向2个高低不同的水池供水,分别做出高、低池供水管路的装置特性曲线,叠加两管路并联运行时的装置特性曲线,与离心泵基本特性曲线的交点即为离心泵运行的工作点.
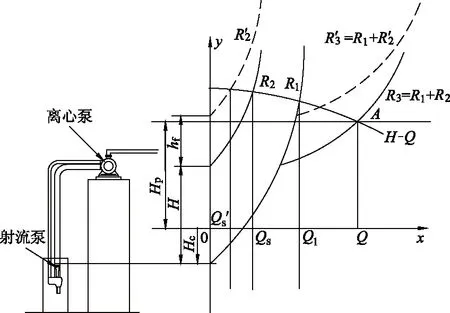
图3 图解法示意
图解法的具体步骤如下:
1) 根据给定的吸上高度及管路材料等,确定进出水管阻力系数.初定射流泵扬程Hc,以Hc所在点水平线作x轴,过Hc点作y轴.
2) 根据不同出口阀开度下出水管的管路特性曲线R′2,做出压力管路特性曲线R1;将R1,R′2横向叠加得两管路并联运行时的装置特性曲线R3.
3) 做曲线R3和曲线H-Q的交点A,得出相应Hc点的工作点参数Q及Hp值;将Qs,Q1等参数代入射流泵的基本方程,反求出射流泵扬程计算值,记为H′c值.
4) 若∣(Hc-H′c)/Hc∣>0.05,则将H′c代替Hc重复步骤1)—4),直至Hc与H′c误差在5%以内;若∣(Hc-H′c)/Hc∣≤0.05,确定点A为联合工作点.
根据计算步骤,得到射流泵装置在吸上高度为4.5和9.0 m时的计算结果,见表2.
表2 不同吸上高度时各工况点的图解法预测结果
Tab.2 Heads predicted by graphic method at different suction heights
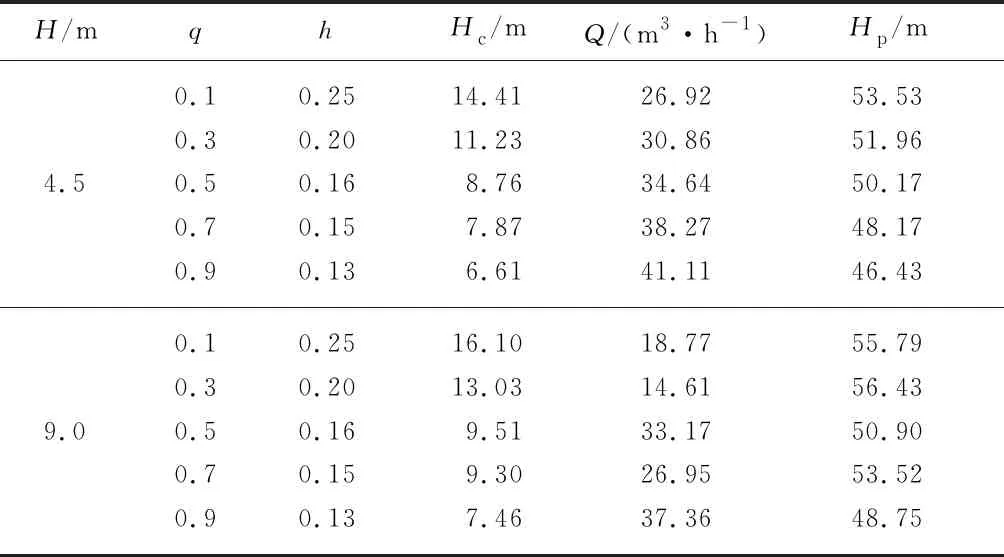
H/mqhHc/mQ/(m3·h-1)Hp/m4.50.10.2514.4126.9253.530.30.2011.2330.8651.960.50.168.7634.6450.170.70.157.8738.2748.170.90.136.6141.1146.439.00.10.2516.1018.7755.790.30.2013.0314.6156.430.50.169.5133.1750.900.70.159.3026.9553.520.90.137.4637.3648.75
2 预测方法精度分析
2.1 试验结果
为了分析预测结果的精度,通过试验比较预测工况点的性能试验结果与预测结果.试验在江苏大学泵检测中心中层及高层平台上进行,2个平台与地下一层平台垂直距离分别为5.0和9.5 m,与水池水面距离分别为4.5和9.0 m.试验台如图1所示.
试验仪器采用电磁流量计,测量误差为±0.5%,压力表精度为0.4级;电动机与离心泵间设扭矩仪,精度为0.5%.回水管出口浸入水池液面,对射流泵吸入口附近水面的影响可忽略不计.通过调节出口阀开度及离心泵转速,得到各工况点性能参数,见表3.
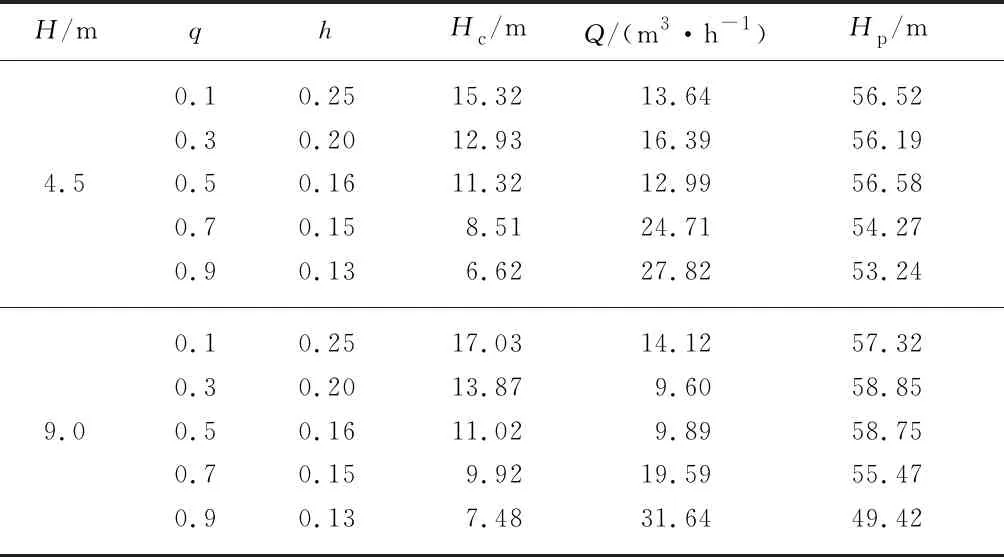
表3 不同吸上高度时各工况点的试验结果
2.2 比较分析
图4为预测法预测结果比较,采用2种方法对不同流量比时射流泵扬程Hc的预测结果与试验结果进行比较,并作误差线,评价2种预测方法的精度.

图4 预测法预测结果比较
Fig.4Hc-qcurves compared between measurements and predictions by two methods
图4a为吸上高度4.5 m的试验结果与2种预测结果,从图中发现,在小流量比工况时,数值解法的预测值接近试验值,而在大流量比工况时,图解法的预测精度要优于数值解法;而在流量比在0.5附近时,相比试验值,2种估计方法预测值均偏低.图4b为吸上高度9.0 m的试验结果与2种预测结果,从图中发现,各条曲线整体略微上移,总体趋势与4.5 m时近似.
总体而言,数值解法整体误差较小,能更好地反映射流泵扬程随流量比q变化的情况,但与试验值相比仍存在误差且个别工况点误差较大,需进一步修正.
3 数值解法预测方法修正
3.1 因子筛选试验
为了提高数值解法的预测精度,修正射流泵扬程Hc的预测值,引入预测值与试验值的比值α作为修正系数.选取可能影响Hc的因子作为影响修正系数α的参数,包括吸上高度、面积比、喷嘴直径[8-9]、流量比、喉嘴距、喉管长径比、泵转速等[10].由于因子数较多且众因子相对于响应变量的显著影响未确定,选择Plackett-Burman试验设计筛选显著因子.
Plackett-Burman试验设计方法主要通过分析比较各个因子两水平的差异与整体的差异,以确定因子的显著性,虽然不能区分与交互作用的影响,但能确定显著影响的因子,从而达到筛选的目的,避免在后期的优化试验中由于因子数太多或部分因子不显著而浪费试验资源.试验设计方法因子高低水平见表4,表中Dn,Dth,Rth为喷嘴直径、喉嘴距、喉管长径比;A,B,C,D为虚拟因子.
表4 Plackett-Burman设计11因子高低水平表
Tab.4 Two levels of 11 factors in Plackett-Burman experimental design

水平H/mmDn/mmqDth/mmRthn/(r·min-1)ABCD19.04.0210.6206.02 9001111-14.52.5130.3104.82 030-1-1-1-1
采用Design-Expert建立Plackett- Burman设计工作表格,根据表格所设定的工况点进行试验,并计算Hc的预测值与试验值的比值,得到各试验点的修正系数α,见表5效应表.
通过方差分析,得到影响修正系数α的主效应,方差分析表见表6.
表5 Plackett-Burman试验设计及结果表
Tab.5 Plackett-Burman experimental design cases and results

编号H/mmDn/mmqDth/mmRthn/(r·min-1)ABCDα11-1-1-11-111-1110.64521-111-1111-1-1-10.83331-1111-1-1-11-111.3384-11-111-1111-1-10.9215-111-1111-1-1-111.089611-1-1-11-111-111.5667-1-11-111-1111-11.2168-1-1-11-111-11110.6419111-1-1-11-111-11.4961011-1111-1-1-11-11.96211-1111-1-1-11-1111.66112-1-1-1-1-1-1-1-1-1-1-11.263

表6 方差分析表
注:*表示差异具有统计学意义(P<0.05);**表示差异具有统计学意义(P<0.01)
从表6可以发现,7个主要因子中仅有面积比和流量比的P值小于0.05,呈现对结果的显著性.进一步对结果进行分析,得到各因素的t值和帕累托图[11-12],如图5所示,图中tcr为t临界值.(H—L表示虚拟因子,仅作参考,故表中未标出)

图5 影响Hc的修正系数α的Pareto效应图
图5表明各因素中,t值超过tcr的为流量比和面积比,其中流量比对修正系数α的影响作用最大,且为正相关,面积比m的影响作用次之,为负相关.其次,吸上高度、喷嘴直径、喉管长径比等对响应的影响依次减小,且t值均远低于tcr,说明影响不具有统计学意义.
3.2 修正系数α的推导
根据以上分析,将影响修正系数α的主效应确定为面积比m和流量比q.通过t软件1stop进行公式拟合搜索,得到面积比m、流量比q与修正系数α的函数关系.在软件的代码本中定义面积比m和流量比q为变量,修正系数α为应变量.输入20组不同工况下试验数据,采用遗传算法中的均匀交叉法,种群数选择20,变异率0.01,交叉率0.85,搜索结果得到的800组关系式中,前132组的相关系数R都超过0.99,满足拟合精度.因此选择其中系数较少、计算步骤相对简单的第6个公式作为修正系数α的计算式,代入系数后,计算式为
(9)
因此,修正后数值解法预测射流泵扬程的计算式为
(10)
式中:Hc,cv,Hc,pv分别为射流泵扬程的修正值和预测值.
3.3 修正公式试验验证
为了验证修正公式的可靠性及适用性,通过不同流量比和不同高度下试验得到的射流泵扬程,与验证公式的计算结果进行比较.因此,在原4.5及9.0 m的试验台基础上分别将液面高度上升了1 m,分别进行不同流量比下吸上高度为3.5 m及8.0 m时的性能试验.对比修正后的数值解法预测得到射流泵扬程,得到不同工况点预测误差,见表7,表中相对误差er=|Hc,pv-Hc,tv|/Hc,tv,其中Hc,tv为试验值.
表7 修正公式预测值与试验值的对比
Tab.7 Comparison of predicted and experimental heads
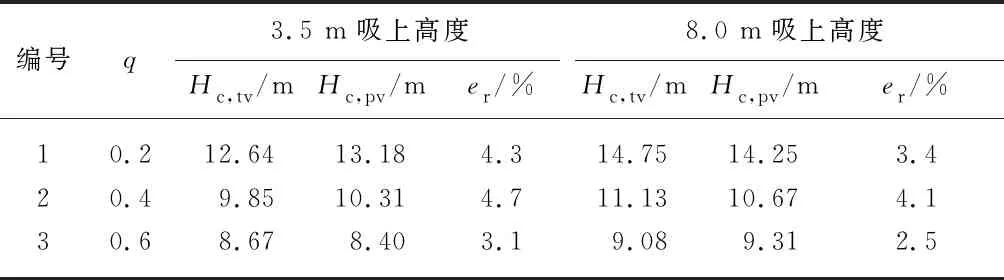
编号q3.5 m吸上高度8.0 m吸上高度Hc,tv/mHc,pv/mer/%Hc,tv/mHc,pv/mer/%10.212.6413.184.314.7514.253.420.49.8510.314.711.1310.674.130.68.678.403.19.089.312.5
通过试验值及预测值的误差计算,发现2种吸上高度各工况点的相对误差都在5%以内,减小了原预测公式在流量比为0.5附近工况点的预测值与试验值存在的较大误差.经修正公式修正后的预测值其预测精度得到了较大的提高.
4 结 论
提出了一种射流泵装置的性能预测方法,得到以下结论:
1) 取射流泵扬程Hc作为关键预测值,通过理论推导的数值解法与利用找特性曲线交点的图解法分别进行预测,结果表明数值解法的预测值整体误差小于图解法的;
2) 为了进一步提高数值解法对射流泵扬程Hc的预测结果,通过Plackett-Burman试验设计筛选出对Hc影响效应显著的面积比m及流量比q作为修正公式的关键参数,利用公式拟合搜索,得到面积比m、流量比q与修正系数α的函数关系;
3) 通过吸上高度3.5和8.0 m的性能试验验证了修正公式的准确性及合理性,试验结果表明各个工况点的相对误差都在5%以内,满足装置性能预测的要求;
4) 修正后的射流泵装置性能预测方法对不同吸上高度及不同工况点的性能预测都有良好的适用性,为射流泵装置的水力设计和不同吸上高度工作时性能预测提供了参考.
研究方法对其他水力机械性能的预测具有借鉴意义.
