4种人工智能模型在江西省参考作物蒸散量计算中的适用性

刘小华，魏炳乾*，吴立峰，杨坡

(1. 西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048； 2. 南昌工程学院鄱阳湖流域水工程安全与资源高效利用国家地方联合工程实验室，江西 南昌 330099)

参考作物蒸散量(ET0)既是计算作物需水量的关键，又是实时灌溉预报和农田水分管理的重要参数.国内外通常以P-M公式作为计算ET0的标准方法[1]，但是对气象数据要求很高，而许多地区很难获取完整的气象数据，故其应用受到限制，于是许多简易方法就得到了广泛应用，例如：基于气温的Hargreaves-Samani(H-S)法[2]，基于辐射的Irmak-Allen(I-A)法[3]、Makkink法[4]和Pristley-Taylor(P-T)法[5]等.李晨等[6]比较了Penman法、Penman van Bavel法和以上4种简易方法在四川省不同气候区的适用性，推荐在东部盆地使用H-S法，其他地区使用P-T法.张倩等[7]评估了Irmak法、H-S以及P-M温度法等8种方法在河南新乡地区的适用性，推荐使用修正后的Imark法.吴立峰等[8]对H-S等多种方法在西北地区的适用性进行了评价，并对参数进行了率定，给出了缺少不同气象资料时的替代方法.

人工神经网络因其独特的并行计算能力、较强的容错能力、自组织和自适应能力等，已经在自然科学等诸多领域得到了广泛应用，并取得了较好的成果.崔远来等[9]利用遗传算法的全局空间寻优功能和BP网络映射能力强的优点，建立了以遗传算法确定最优网络结构的进化神经网络模型用于预测ET0.段春青等[10]基于混沌遗传程序设计建立的ET0预测模型，预测结果较好.徐俊增等[11]考虑ET0时间序列规律性，建立了基于气象预报资料的ET0神经网络预测模型，模型实用性得以提高.顾世祥等[12]针对天气复杂地区建立了具有模糊集运算的逐日ET0预测模型，对提高预测精度有着极佳的效果.许多其他算法例如径向基函数神经网络[13]、广义回归神经网络[14]、列文伯格-马夸尔特法[15]、模糊推理系统[16]等都在预报ET0方面得到了应用.然而，尽管人工智能模型在预报ET0方面已有不少研究结果，但模型的适用范围多为局部地区，模型参数具有地域性特征，并且缺少适宜江西地区的系统解决办法.

文中在前人研究基础之上，以P-M法计算的ET0为标准值，通过对比多层感知器ET0计算模型、多元自适应样条ET0计算模型、广义回归神经网络ET0及支持向量机ET0计算模型在不同气象资料组合下的模拟精度，从中选择适宜江西地区的最优模型，并获得气象资料不全时参考作物蒸散量简化计算法，以期为江西省农业灌溉制度制定和水资源优化配置提供支撑.

1 材料与方法

1.1 试验区概况

江西省位于长江中下游南岸，赣北为鄱阳湖平原，赣中、南部以丘陵为主，东西两侧以山地为主.气候属中亚热带温暖湿润季风气候，多年年均气温为16.3～19.5 ℃，一般自北向南递增.江西省年降雨量为1 341～1 943 mm，河川径流主要靠降雨补给，故季节变化较大，汛期河水暴涨，容易泛滥成灾；又因江西为水稻种植基地，河水泛滥易使水稻产量下降.省内水资源时空分布不均，加大了水资源开发利用的难度，实际有效灌溉面积仅有41.2万hm2，农业灌溉水利用系数为0.45，远低于发达国家的农业灌溉水利用系数0.8.

1.2 数据来源

选取的江西省南昌、吉安、龙南3个站的每日气象资料(包括总辐射量、日照时数、20:00-20:00降雨量、平均气温、最高气温、最低气温、相对湿度和2 m高风速)来源于中国气象科学数据共享服务网地面观测数据中的日值数据集(见“国家气象信息中心”：http://data.cma.cn/).虽然数据集数据已经经过严格的质量控制，但为了比较不同ET0估算法的精度，故对气象资料不全的该日全部数据予以剔除.

1.3 研究方法

1.3.1 多层感知器模型

Rumehar等提出的多层感知器(MLP)模型[17]是一种前馈人工神经网络模型，由一组输入向量反射到一组输出向量.该方法的具体思想：设某层中某一神经元j的输入为netj，其输出为yj，与此层相邻的低层中任一神经元i的输出为yi，则有

(1)

和

yj=[1+e-(netj+hj)/θ0]-1，

(2)

式中：wij为神经元j与神经元i之间的连接权；hj为神经元的阈值；θ0用以调整函数的陡度[18].

1.3.2 多元自适应样条

多元自适应回归样条法(MARS)是一种专门针对高维数据拟合的回归方法，是模拟变量之间的非线性和相互作用的线性模型的扩展，其一般形式为

(3)

模型建模的第1步是迭代过程，模型先生成初始基函数(迭代次数I=0)，即B0(x)=1每次迭代(I>1)，遍历所有的节点，成对地添加新的以减小误差最多的镜像基函数，直到基函数个数达到最大或者模型精度满足

B2I-1(x)=Bi(x)b(xv,t)，

(4)

B2I(x)=Bi(x)b(-xv,t)，

(5)

式中：Bi(x)为在迭代中生成的基函数，称作父基函数；b(xv,t)为相应基函数的决策系数.

第2步是每次循环删除1个误差减小量最小的基函数，得到对应的子模型，直到模型只剩下截距项，引入广义交叉验证GCV准则如式(6)，最终选取GCV值最小的子模型为最优模型进行模拟.

(6)

C(N1)=N1+1+dN1，

(7)

式中：m为输入的变量个数；N1为模型的有效系数个数；d为惩罚因子，一般取2～4.

1.3.3 广义回归神经网络

广义回归神经网络(GRNN)于1991年由SPECHT提出[19]，是径向基网络的一种.它由1个径向网络层和1个线性网络层组成，以样本数据为后验条件，执行Parzen非参数估计，从观测样本中求出自变量和因变量的联合概率密度函数，直接计算因变量对自变量的回归值，依据概率最大原则计算网络输出[20].

文中使用不同输入参数的GRNN模型，可在Matlab中直接调用GRNN函数，其调用格式为net=newgrnn(P,T,SPREAD)，其中P为Q组输入向量组成的R×Q维矩阵；T为Q组目标向量组成的S×Q维矩阵；SPREAD为径向基函数的扩展速度，默认取1[21].

1.3.4 支持向量机

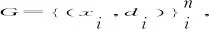
f(x)=wφ(x)+b，

(8)

式中：φ(x)是向量空间x的高维超平面；w和b的值通过结构风险最小化确定.

1.4 统计评价与数据处理

统计评价运用以上各方法计算参考作物蒸发蒸腾量的计算精度，常用均方根误差(RMSE)、决定系数(R2)、纳什效率系数(NSE)等评价指标，其计算式为

(9)

(10)

(11)

若计算精度越高，则RMSE越接近0，R2和NSE越接近于1.

2 结果与分析

2.1 智能模型的日值对比

为了检验4种智能模型在江西省ET0计算中的适用性，将南昌、吉安、龙南3个站点1966—2015年每日最高气温(Tmax)、最低气温(Tmin)、日照时数(n)、相对湿度(RH)和2 m高风速(u2)作为输入参数，分别计算了不同气象要素组合条件下的参考作物蒸散量，并结合P-M公式的计算结果进行验证.3个站点各模型在不同气象要素组合方式下的ET0计算精度评价见表1.

表1 各站的精度评价结果

从表1可知，对于南昌站，MLP模型中MLP1组合的均方根误差RMSE(0.232 mm/d)最小，模型效率系数NSE(0.980)和相关系数R2(0.982)最大；而其他组合的RMSE略有增大，NSE和R2略有减小.RMSE越接近于0，说明模型误差越小；NSE和R2越接近于1，说明模型模拟精度越高，故认为MLP1的模拟精度最好.同理可知其他3种模型中第1组合MARS1，GRNN1，SVM1的模拟精度也为最好.对于吉安和龙南站，与南昌站类似，也是各模型的第1组合MLP1，MARS1，GRNN1，SVM1的误差最小，模拟精度最高.

综上可知，对于3个站点的4种人工智能模型，输入数据完整时组合1的模拟精度最高，适用性强；输入数据为Tmax，Tmin，n，u2的组合2和输入数据为Tmax，Tmin，n，RH的组合4的模拟精度次之；输入数据为Tmax，Tmin，u2，RH的组合3的模拟精度低于输入数据仅有Tmax，Tmin，n的组合5；输入数据仅有n，u2，RH的模型误差较大，其适用性差.

为了比较4种智能模型的差异，基于RMSE最小的顺序对4种模型的6种参数组合进行排序，结果如表2所示，可以看出3个站在6种参数组合下MARS模型的RMSE均最小，排第1位；SVM模型的RMSE均比GRNN和MLP模型的小，排第2位.在不足6种的参数组合下，GRNN模型的RMSE比MLP的小，排第3位，MLP模型排第4位.

针对3个站北部南昌、中部吉安及南部龙南，基于RMSE的平均排序，可知4种模型中MARS模型的RMSE最小，其次是SVM模型，GRNN模型为第3，MLP模型的RMSE最大.6种组合条件下，由4种模型在3个站点的应用，可知MARS模型适应性最好，MLP模型适应性较差.

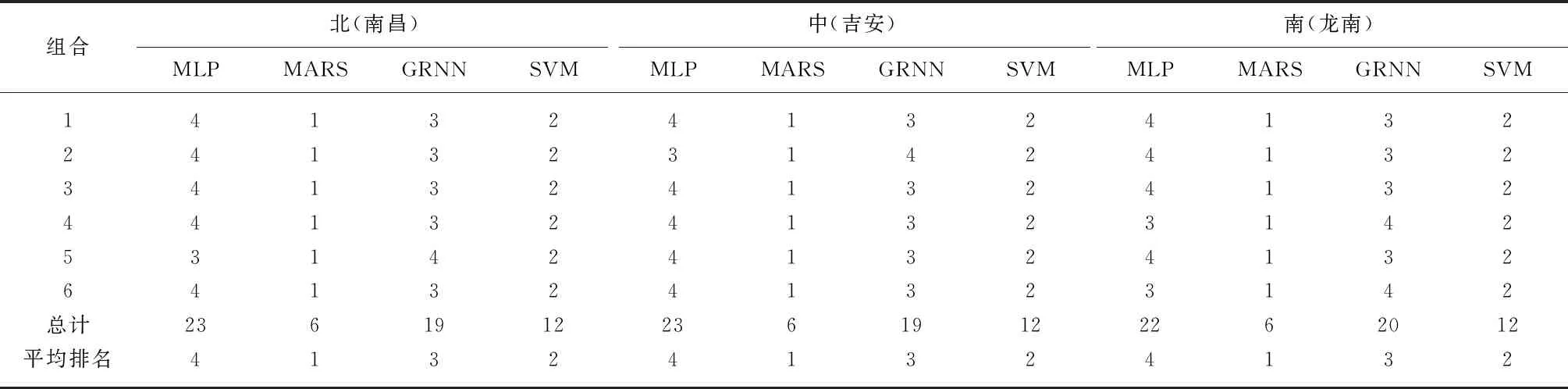
表2 基于RMSE的各站模型排序

2.2 智能模型结果与P-M结果比较

图1为龙南站MLP模型在6个不同组合下的参考作物蒸散量ET0模拟值与P-M法计算结果的对比.

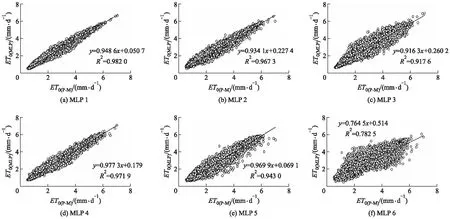
图1 龙南站MLP模型与P-M的ET0对比

从图1可知，组合MLP1的模拟精度最高，可适用于参考作物蒸散量的模拟，而缺少某些气象资料的其余组合模拟精度有所降低；MLP2(Tmax，Tmin，n，u2)，MLP4(Tmax，Tmin，n，RH)的模拟精度稍逊于MLP1，说明RH和u2对模型模拟ET0的影响较小，在缺少RH和u2资料时可选用该模型模拟ET0. MLP5(Tmax，Tmin，n)的精度高于MLP3(Tmax，Tmin，u2，RH)的，说明日照时数对于模拟蒸散量的影响大于风速和湿度的影响.MLP6(n，u2，RH)组合中由于缺少温度数据，精度最差，说明温度对模型的影响最大.龙南站应用其他3个智能模型模拟不同组合下的蒸散量与P-M结果进行对比的结果也与MLP模型相同.

江西省由北向南的日照时数与湿度大致相同，主要区别在于温度，而风速对模型的计算结果影响较小.对于中部的吉安站和北部的南昌站，其结果与龙南站一样，这说明4种智能模型在不同区域含有温度要素组合的计算精度均较高.因此认为在含有温度的气象组合条件下，4种模型均适用于全省任意地区的ET0计算.

2.3 智能模型与经验法比较

由于组合2(MLP2，MARS2，GRNN2，SVM2)与PVB经验法的输入数据相同，组合5(MLP5，MARS5，GRNN5，SVM5)与I-A，Makkink，P-T法的输入数据相同，故将智能模型组合分别与输入相同数据的经验法进行比较，以说明智能模型在计算ET0中的优越性与准确性.

经验法(P-T，I-A，Makkink和PVB法)的计算精度见表3，其中PVB法的精度最差，其RMSE大于表1中4种智能模型组合2(MLP2，MARS2，GRNN2，SVM2)的RMSE，且NSE和R2均小于智能模型；P-T，I-A和Mak法的精度相对较高，但与4种智能模型组合5(MLP5，MARS5，GRNN5，SVM5)相比RMSE仍较大，且R2和NSE均小于智能模型，由此说明4种经验法的模拟精度均低于输入相同数据的智能模型，故建议在该地区使用智能模型法.

表3 经验法计算精度一览

3 结 论

以江西南昌、吉安、龙南3个站点1966—2015年每日最高气温、最低气温、日照时数、相对湿度和2 m高风速作为输入参数，以P-M公式的计算结果为对照，建立了6种不同气象要素组合条件下的4种ET0计算模型，并与经验法进行对比，得出了以下结论：

1) 统计结果表明，在相同输入资料条件下，4种智能模型中MARS法模拟精度最高，其次是SVM，GRNN和MLP法.MARS法计算简便可直接使用，是4种方法中最优的ET0计算方法.

2) 当4种模型的输入数据完整时，模型的模拟效果最好，此时的4种模型均可推荐用于ET0的模拟；当4种模型的输入数据仅有最高温度、最低温度、日照时数、风速或者最高温度、最低温度、日照时数、相对湿度时，模拟精度较高，可作为气象要素缺失条件下的推荐方法；当4种模型的最高、最低气温数据缺少时，模拟效果极差，不推荐使用.各气象要素对4种模型模拟ET0的影响由大到小按要素排序依次为最高和最低气温、日照时数、相对湿度、风速.

3)在3个站点中，4种智能模型的ET0计算精度均优于相同输入数据下的经验法，各经验法的RMSE为0.366～0.845 mm/d，而相同输入数据下的智能模型的RMSE为0.272～0.326 mm/d，经验法模拟精度均低于相同输入数据条件下的4种智能模型，表明了4种智能模型在江西的模拟精度优于经验法.