旋转弹控制耦合的分数阶滑模解耦
2020-01-03戴树涛陈华兵程养民杨宇星
戴树涛,陈华兵,程养民,杨宇星
(西安航天动力技术研究所,陕西 西安 710025)
0 引言
导弹武器或运载火箭采用旋转体制能够提升稳定性,有利于提高导弹克服诸如推力偏心、起控点散布、质量分布不均匀、随机阵风等干扰的能力[1]。为提升旋转导弹的过载能力,因此产生了旋转导弹双通道控制,以解决传统单通道控制的过载能力不足[2]。但是旋转体制同时也会带来俯仰、偏航双通道的交叉耦合[3],这些耦合主要包括陀螺惯性耦合、马格努斯气动耦合以及舵系统控制耦合。耦合会对控制系统的工作造成不利的影响,严重时甚至会导致失稳,因此解耦成为旋转弹控制系统设计的首要问题。在这些耦合因素中,运动学耦合造成的通道间耦合往往较小,且随自旋转速的变化不大,所以双通道解耦的重点就是消除舵系统的控制耦合[4]。闫晓勇等人基于一阶舵系统模型设计了指令超前补偿解耦控制器[5],实现了舵系统的解耦。李永亮通过研究十字型鸭翼旋转弹模型[6],对一阶舵系统模型设计了前置补偿器,实现了鸭式舵系统的解耦。总的来说,这些传统解耦方法的思路都是基于舵系统传递函数矩阵,通过前馈补偿、指令超前补偿等多变量频域方法设计解耦控制器实现对角占优,使得传递函数矩阵的非对角元素为0或者近似为0,从而达到解耦的目的。但以上方法的最大问题在于需要对传递函数矩阵进行复杂且计算量较大的求逆运算,如果传递函数矩阵的阶次较高或者系统模型复杂,求逆操作往往不易实现。而且在求逆计算中,易出现矩阵接近奇异使得求逆运算的结果已不可采用的情况。除此之外,基于频域方法设计的解耦控制器只能实现系统稳态条件下的静态解耦,且一旦舵系统参数发生摄动或者自旋转速产生变化,解耦效果便难以保证。
为解决以上问题,本文基于更为贴合工程实际的二阶舵系统模型,通过推导旋转舵系统的状态空间表示,采用分数阶微积分理论和滑模变结构控制理论来设计舵系统的解耦控制器,以避免对传递函数矩阵求逆。仿真结果表明,滑模解耦能够提升解耦控制系统对参数摄动和转速变化的鲁棒性,采用分数阶微积分理论能够减小滑模控制方法的抖振。
1 舵系统的模型及耦合分析
1.1 舵系统的二阶状态空间模型
为避免自旋造成的不便,旋转弹的建模往往基于准弹体系,而舵系统是在旋转的弹体系下生成舵偏角[7],故先将弹体系下的舵系统输入输出信号投影到准弹体系下。弹体系和准弹体系下舵偏角的关系如图1所示。
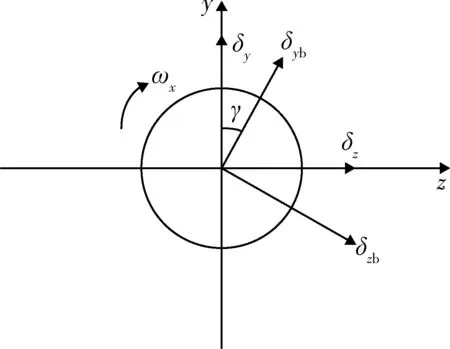
图1 弹体系和准弹体系下舵偏角关系图
图1中δzb和δyb分别为弹体系下俯仰舵偏角和偏航舵偏角,δz和δy分别为准弹体系下俯仰舵偏角和偏航舵偏角。假设滚转角为γ,由准弹体系到弹体系下的舵系统指令变换关系为
(1)
为了分析问题的简化,作以下假设:忽略导弹滚转通道的动态变化过程,并且由于导弹旋转转速的变化较缓慢,可假设导弹滚转速度ωx不变,对式(1)求一阶导数如下:
(2)
对式(2)再求导如下:
(3)
弹体系下舵机的系统模型一般表示为二阶传递函数:
(4)
式中:Ts为舵机的时间常数,μs为舵机的阻尼系数,这2个参数为舵机的重要参数,受舵机硬件水平的限制。则根据式(4)可知弹体系下舵机的输出舵偏角向量δb=(δzb,δyb)T与舵机的输入信号δbc之间的关系如下:
(5)
将式(2),(3)代入到式(5),并根据式(1)将指令投影到准弹体系下,可得
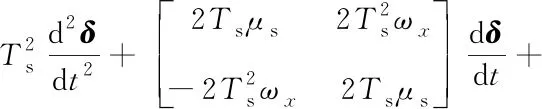
(6)
式中:δ=(δz,δy)T和δc=(δzc,δyc)T分别为准弹体系下的舵机输出信号和输入信号。
为了得到准弹体系下舵机的状态空间模型,选取状态向量x=(x1,x2,x3,x4)T,各分量如下:
(7)
选取输出向量y=(y1,y2)T,各分量为
(8)
可得舵机的状态空间模型为
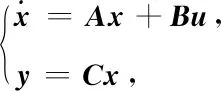
(9)
式中:u为解耦后舵系统的输入信号,若没有解耦控制器,则u=δc;
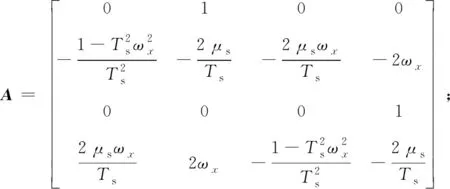
1.2 舵系统的耦合特性分析
为了便于分析舵系统的耦合特性,对式(6)进行拉普拉斯变换,得到准弹体系下舵机传递函数矩阵为
(10)
式中:
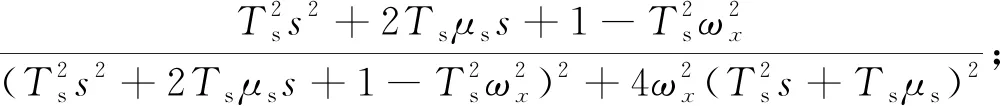
由传递函数矩阵可以发现,当弹体的滚转速度为0时,即弹体不滚转时非对角元素为0,此时不存在耦合。弹体滚转使得舵系统的阶次由二次变为四次,增加了系统的复杂性,且此时舵系统的频带与弹体滚转速度相关。
为分析转速对耦合效应的影响,使用Matlab软件对舵系统模型进行仿真,舵机参数如表1所示。

表1 舵机参数取值
分别给定俯仰舵指令信号为单位阶跃信号和频率为2 Hz,幅值为1的正弦信号,绘制出转速分别为3,5,10 r/s时的偏航舵响应信号曲线如图2,3所示。
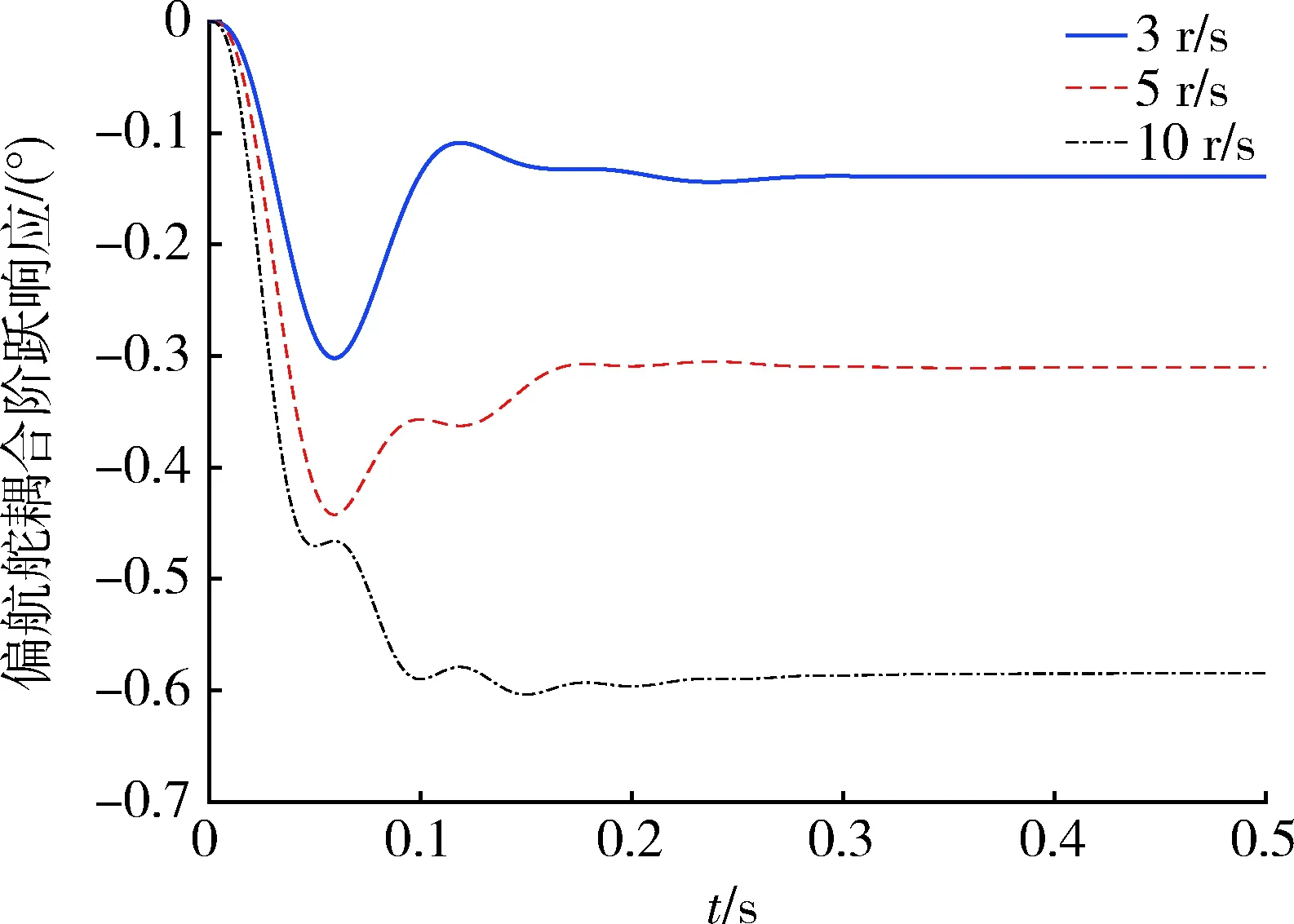
图2 偏航舵耦合阶跃响应
由图2可得出,转速越大,控制耦合越严重。对本舵机参数而言,转速3 r/s时稳态耦合量约为15%,转速5 r/s时稳态耦合量约为32%,转速10 r/s时稳态耦合量约为60%。

图3 偏航舵耦合正弦响应
由图3也能看出转速越大,耦合程度越大,并且舵系统延迟时间也越长。
综合以上分析可以得出,控制耦合的程度与弹体滚转速度呈正相关,且耦合越剧烈,舵系统延时越长。
2 滑模变结构解耦控制器
为改善转速和参数变化下传统解耦方法效果差的问题,采用滑模变结构理论设计解耦控制器,其解耦控制结构图如图4。

图4 解耦回路图
以δc=(δzc,δyc)T为舵指令信号,δ=(δz,δy)T为舵输出信号。令e1,e2为跟踪误差,则e1=δzc-δz,e2=δyc-δy,故解耦控制的目标即使得e1=e2=0。令e=(e1,e2)T,取滑模面函数为

(11)

对式(11)求导,可得
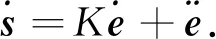
(12)
采用指数趋近律,为减少抖振趋近律中采用饱和函数,饱和函数表达式如下:
(13)
式中:Δ为正数。
设计趋近律如下:
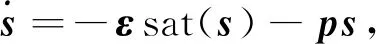
(14)


(15)
由式(9)可推得:

(16)
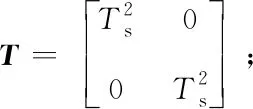
将式(15)与式(16)联立,可得到设计的滑模控制律为
(17)
3 分数阶滑模解耦控制器
滑模控制器虽然具有很多优点,但也存在固有的抖振问题,这不利于工程实际应用。使用分数阶微积分算子代替滑模控制器设计中变化剧烈的整数阶导数项,有利于减小滑模控制的抖振,因此使用分数阶微积分理论对滑模控制器进行优化。
3.1 分数阶算子的近似方法
目前,尽管一些学者对分数阶微积分控制器做了相关研究[8-11],分数阶理论在数学上还是较难直接实现的,无法求得其精确值,主要还是采用有限的整数阶微积分近似逼近。Outstaloup A提出了Outstaloup递归滤波器的有理化近似法[12],该方法率先提供了一种分数阶算子的实现途径,为其他方法的产生奠定了理论基础。因整数阶微分的幅相特性随频率变化,因此在近似逼近时要选定一个频段。假定滤波频带为(ωb,ωh),则可以构造Outstaloup滤波器为
(18)
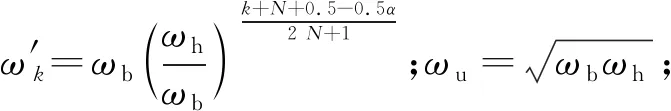
由于该方法的近似效果一般,因此也有其他学者提出了逼近方法,其中东北大学薛定宇教授等人在Outstaloup滤波器的基础上提出了改进的Outstaloup滤波器法[13]。令
(19)
式中:α为分数阶次,0<α<1;b>0;d>0。
对L(s)进行一阶Taylor展开,整理可得
(20)
本文采用改进型Outstaloup滤波器来近似分数阶算子。
3.2 分数阶滑模解耦控制器
取滑模面函数为
s=Ke+Dαe,
(21)
式中:Dα为分数阶微分算子,表示求α次导数,0<α<1。对式(21)求导,得
(22)
按照式(14)设计趋近律,并进行类似于前述的推导过程,可得出控制律为
D1-α(εsat(s)+ps)).
(23)
4 仿真校验
4.1 仿真过程及参数
设导弹自旋转速为3 r/s,舵机参数如表1所示。需要说明的是,表1中舵机参数的选取不能随意设置,因为旋转导弹弹体固有频率fn、自旋频率fx和舵系统带宽fb之间应满足以下关系[14]:
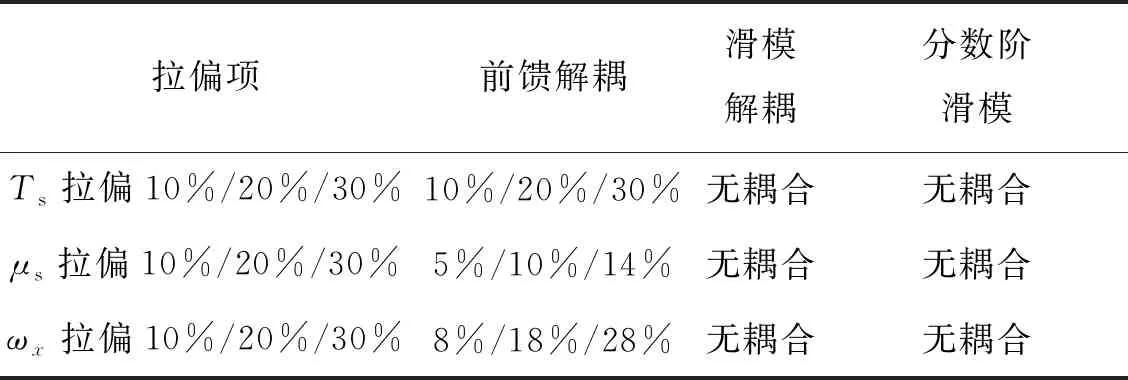
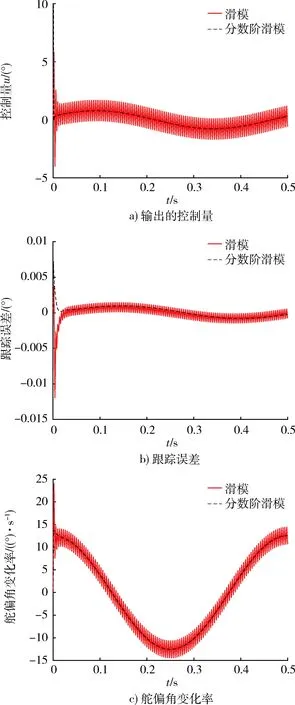
1.8fn (24) 否则会引起系统共振,导致灾难性后果。因fx=3 Hz,取fb=8 Hz,则ωb≈50.880 8 rad。 根据二阶系统带宽计算公式[15]: (25) 取阻尼系数μs=0.5,可推出ωs≈40,故Ts=1/ωs=0.025。 按照式(17)的设计思路搭建模型进行仿真,滑模解耦控制器各参数取值如表2所示。 表2 滑模解耦参数取值 按照式(23)的设计思路搭建模型进行仿真,分数阶滑模解耦控制器各参数取值如表3所示。 表3 分数阶滑模解耦参数取值 将俯仰舵指令信号设为单位阶跃信号,偏航舵指令置0,将前馈解耦方法、滑模解耦方法、分数阶滑模解耦方法3种方法舵输出信号的仿真曲线绘制如图5,并将图5的定量分析结果绘制如表4。 图5 标准参数值下3种解耦方法响应对比 表4 图5结果对比 由图5和表4可知,滑模解耦和分数阶滑模解耦能够消除响应的超调量和稳态误差,响应速度仅为0.03 s,其解耦精度比传统前馈解耦更高。 将俯仰舵指令信号设为单位阶跃信号,偏航舵指令置0。为验证滑模解耦控制器对参数摄动的鲁棒性,分别将舵机的时间常数、阻尼系数和弹体转速拉偏10%,20%和30%,将前述3种方法的偏航舵耦合输出信号的仿真曲线绘制如图6,定量结果如表5。 图6 参数拉偏下3种解耦方法偏航舵耦合对比 由图6和表5可知,前馈解耦方法对参数变化无鲁棒性,滑模解耦能够抑制30%的参数偏差所引起的不利影响。还可发现Ts和ωx的变化对前馈解耦的效果影响较大,而μs的变化对前馈解耦的效果影响较小。 表5 图6参数拉偏下耦合输出量对比 图7 两种滑模方法的结果对比 由图7可知,采用传统滑模方法,稳态控制量抖振幅值为1左右,舵偏角变化率抖振幅值为2左右,这些抖振均不利于舵系统安全稳定工作。采用分数阶滑模解耦能够消除控制量和舵偏角变化率的抖振,以保护舵系统,且能够减小跟踪误差,提高跟踪精度。 本文针对旋转弹箭双通道舵系统的解耦问题,为解决传统频域补偿方法需要求逆和对参数摄动鲁棒性差的问题,设计了滑模解耦控制器,并且为抑制滑模方法的抖振,引入了分数阶微积分理论,设计了分数阶滑模解耦控制器。仿真结果表明,所设计的解耦控制器能够满足舵机系统的解耦要求,且能够解决传统解耦方法存在的问题,具备一定的工程应用价值。

4.2 仿真结果及分析
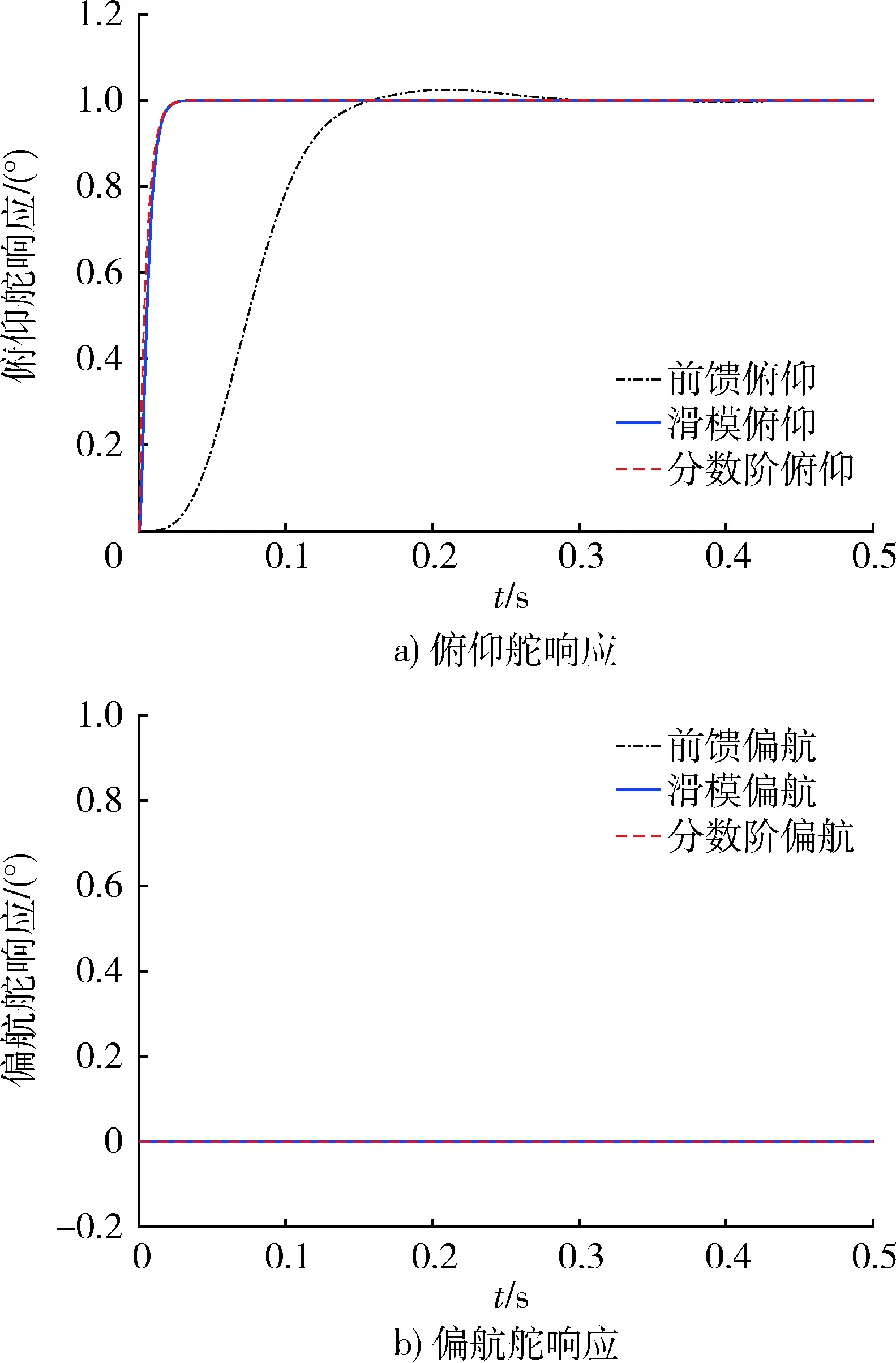
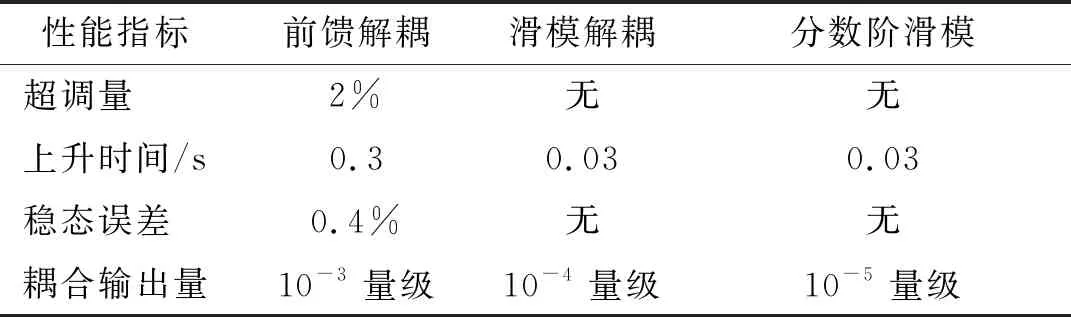

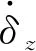
5 结束语
