基于F-GERT网的OODA环交战链路效益评估方法

张明智，夏璐,2

(1.国防大学 联合作战学院，北京 100091；2.中国人民解放军95948部队，甘肃 兰州 732750)

0 引言

体系对抗过程中，交战链路的作战效益决定了体系整体涌现出的作战效果。这种交战链路从体系感知单元发现目标开始，通过不断侦察、监视，确认目标后由决策单元发出打击指令，再由火力单元摧毁目标并反馈打击效果。正是交战链路的反复循环，形成各种网络化对抗场景，产生体系作战效能。美国的John R.Boyd对这种交战链路循环进行了抽象，称之为OODA环，它将作战过程概括为“观察(observe)—判断(orient)—决策(decide)—行动(act)”这4种行动的不断循环，从而得出破击体系的关键在于破坏敌对方体系的OODA环的结论[1-3]。

OODA环的研究目前多集中于对其循环时长、鲁棒性等特征的研究[4-5]，而对于其抽象出来的作战过程链路信息转化效果的分析评估，由于链路连接关系的随机性、评价指标的模糊性，尚未有一种有效的方法进行描述、表示及建模。本文针对OODA环交战链路效益评估问题，借鉴图示评审技术(graphical evaluation and review technique,GERT)网建模技术，尝试运用三角模糊数描述交战链路活动评价参数，在此基础之上，构建可评判交战链路活动参数传递效应的评估模型，并通过案例验证相关模型的应用效果。

1 相关概念

1.1 GERT网络

GERT是一种广义随机网络分析方法，广泛应用于项目计划管理、供应链评价、应急管理等领域[6-8]。GERT网的本质属性为线性系统，因此，可以基于信号流图模型，运用梅森公式和矩母函数对GERT网络各节点之间存在的传递关系进行解析计算[9]。

根据GERT网络理论，对于随机变量参数x及任意实数s，随机变量x的矩母函数

M(x,s)=E(esx)=

(1)

式中：f(x)为当x为连续型随机变量时的概率密度函数；P(x)为当x为离散型随机变量时的概率分布函数。

设一个链路活动(i,j)定义为由节点i向节点j的传递过程，则该链路活动参量x在GERT网络模型中的传递函数Wij(x,s)=PijMij(x,s)，Pij为该链路活动实现的概率，如图1所示。

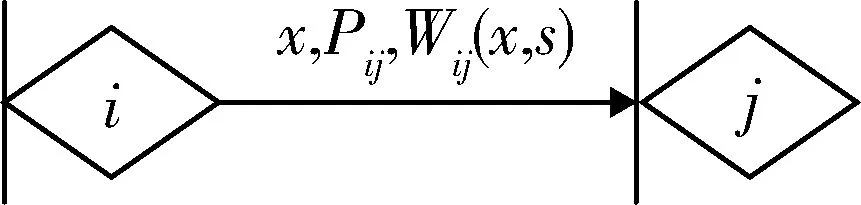
图1 GERT网络链路活动(i,j)

GERT网络中的链路结构一般包括串联、并联和回路3种情况，如图2所示，可证：

对于串联结构，节点i与k之间传递函数：

Wik(x,s)=Wij(x,s)Wjk(x,s)=

PijPjkMij(x,s)Mjk(x,s).

对于并联结构，节点i与j之间传递函数：

对于回路结构，节点i与j之间传递函数：

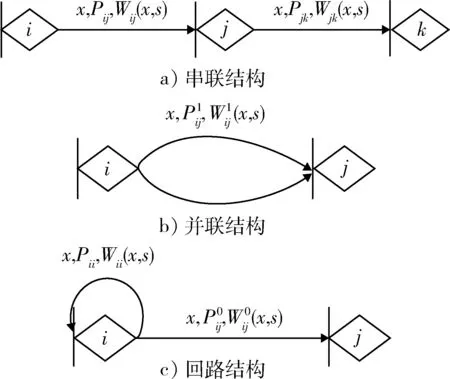
图2 GERT网络串联、并联和回路结构

1.2 三角模糊数

根据上述基本法则，后续可进行三角模糊数复杂运算的推导、计算。

2 基于F-GERT网的OODA环交战链路效益评估模型构建

2.1 OODA环交战链路活动参数模糊评价矩阵

OODA环交战链路活动实现的是从感知到决策再到火力的信息流优势转化过程。对这种信息流转活动进行评价通常包括3项指标参数，即时敏特征α、容量特征β和偏移特征γ。

时敏特征α反映的是OODA环交战链路中某2个节点之间信息状态转移活动对信息流动时间的敏感性，例如搜索探测时长等。

容量特征β反映的是OODA环交战链路中某2个节点之间信息状态转移活动对信息传输通路容量的需求，例如网络通信带宽等。

偏移特征γ反映的是OODA环交战链路中某2个节点之间信息状态转移活动对信息传递精度的需求，例如导航定位精度等。

对于上述3项指标参数的描述可以在结合大量装备试验以及部队演习训练测量数据基础上，结合领域专家的经验知识，通过专家评分法给出其特征参数的优劣，并基于三角模糊数进行表示。因此，对交战链路活动时敏特征α、容量特征β和偏移特征γ等可用三角模糊数评价矩阵表示为

(2)

2.2 OODA环交战链路F-GERT网模型

OODA环从“观察(observe)”到“行动(act)”的交战链路，可以看作是信息流在GERT网中的随机传递过程，某个传递活动相关参量的优劣可以用X来表示，且其可以看作为离散型随机变量。因此，可以根据GERT网络中传递函数、链路活动概率以及矩母函数等模型，结合三角模糊数理论，构建OODA环交战链路F-GERT网模型。

得证。

得证。

证明：由三角模糊数的定义可知xL≤xM≤xU，对于函数f(x)=ekx，当k≥0，f(x)单调递增，当k<0，f(x)单调递减，结合法则3可知

得证。

根据推论3，容易得到，对于任意实数sα，OODA环交战链路时敏特征α的模糊评价参量xα的矩母函数

(3)

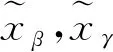
(4)

式中：sα，sβ，sγ为任意实数。

证明：令s，sα，sβ，sγ为任意实数，则

证毕。

(5)

等效矩母函数为

(6)

证明：由GERT网理论可知，链路中起点到终点的等效传递概率为其等效传递函数将任意实数s全部置0时的取值。

所以

证毕。

定理1和定理2即为OODA环交战链路F-GERT网计算的基础原则。

2.3 OODA环交战链路效益评估模型

OODA环交战链路从发现目标传输信息开始到稳定跟踪并运用火力摧毁目标结束的整个过程中信息活动平均传递次数决定了OODA环链路活动的效率，而从OODA环链路活动起点到终点的效益累积评估结果则决定了OODA环时敏特征、容量特征和偏移特征在链路源节点与终节点之间活动传递的参数累积效应。

(7)

式中：

(8)

3 基于F-GERT网的OODA环交战链路效益评估流程

评估基于F-GERT网的OODA环交战链路效益关键在于获取所需评估链路源节点与终节点之间的等效传递函数[15-16]，并综合运用三角模糊数对信息流活动进行评价及计算。具体流程如下：

Step1选取需要分析的OODA环F-GERT网交战链路，遍历其节点(假设节点总数为n)及其连接关系，获取节点之间传递函数关系分析矩阵

1 …n

式中：矩阵元素Wji(i=1,2,…,n;j=1,2,…,n)为节点j到i的传递函数。

Step2获取需要分析的OODA环F-GERT网交战链路源节点与其他非源节点之间的等效传递函数矩阵Q。在An×n中删除源节点对应的行和列后剩余元素构成的矩阵令其为M；在An×n中提取源节点对应列的元素构成矩阵，并在该矩阵中删除源节点对应的行，剩余元素构成的矩阵令其为Y;根据信号流图原理可得Q=(I-M)-1Y，其中I是与M阶数相同的单位矩阵。

Step3通过专家评分法给出需要分析的OODA环F-GERT网交战链路信息流转活动时敏特征α、容量特征β和偏移特征γ的三角模糊数评价值以及相应的权重数值。

4 应用案例分析

设某OODA环交战链路节点分别由卫星、空中预警平台、指控中心、陆上探测搜索平台、陆上火力制导平台、地空导弹、空中探测搜索平台、空中火力控制平台、空射导弹等信息流转载体构成，在 F-GERT 网链路模型中节点序号分别记为1，2，3，4，5，6，7，8，9，如图3所示。各节点之间信息流活动传递函数用Wij表示。

图3 OODA环F-GERT网链路

图3中OODA环信息流转活动各评估指标三角模糊数取值如表1所示，时敏特征α、容量特征β和偏移特征γ的权重分别为：ωα=0.35，ωβ=0.25，ωγ=0.4。

表1 OODA环F-GERT网链路活动评估指标值

(1) 分析陆上火力打击链路效益

根据Step 1和Step 2，可以得到从链路活动起点1到终点6的等效传递函数为

根据式(5)可求得该OODA环陆上火力打击链路等效传递概率为

根据式(7)可求得该OODA环陆上火力打击链路信息活动平均传递次数为

5.602 9.

根据式(8)以及三角模糊数的计算法则可求得OODA环陆上火力打击链路效益综合评估因子为

(2) 分析空中火力打击链路效益

同理，根据Step 1和Step 2可求得从链路活动起点1到终点9的等效传递函数为

根据式(5)可求得该OODA环空中火力打击链路等效传递概率为

根据式(7)可求得该OODA环空中火力打击链路信息活动平均传递次数为

根据式(8)以及三角模糊数的计算法则可求得OODA环空中火力打击链路效益综合评估因子为

5 结束语

OODA环交战链路效益直接决定了体系作战能否实现由感知到决策再到火力的优势转化。在武器装备平台性能相同或代差不大的情况下，提升OODA环交战链路的作战效益将有助于联合作战体系正向涌现出整体合力。本文针对OODA环交战链路效益评估问题，运用GERT网络理论和三角模糊数方法，构建了基于F-GERT网的OODA环交战链路效益评估模型，提出了运用F-GERT网进行OODA环交战链路效益评估的流程。后续可进一步以OODA环交战链路效益综合评估因子最优为目标函数，研究可用于交战链路集优选的模型及方法。