迷宫物语——安藤忠雄的几何叙事路径

张海峰 季翔，2

1 中国矿业大学

2 江苏建筑节能与建造技术协同创新中心

1 抽象与具象的重合

关于如何实现建筑的物质性与人的使用性的调和以及建筑的抽象与具象性的问题，安藤忠雄一直都在思考。他在《抽象与具象的重合——阿尔巴斯和皮拉内西》一文中“将J·阿尔巴斯的纯几何学作品（图1）与G.B皮拉内西的非常复杂的、非日本的、表现立体空间的《幻想的牢狱》的作品进行了对比（图2），以此来思考所追求的理想建筑表现。J·阿尔巴斯运用了严谨的几何学，在看似简洁的作品中，彻底追求了作品的抽象性，从而获得了‘暧昧’所带来的多种自由。对于建筑形态，我也采用了严谨的几何学形态，从中追寻皮勒奈基的幻性迷路空间，构筑了具象化的建筑。对我来说，建筑是表现具象性与抽象性的并存之物。[1]”

在安藤看来，建筑是抽象与具象的重合，此处的抽象指隐藏在皮拉内西监狱混乱背后的几何秩序，而具象就如同监狱表象性的迷幻空间。最终呈现的是这样一个结果：安藤在抽象几何秩序中几何纯化的个性表达以及具象性迷宫般路径的呈现方式，二者重合产生具有代表性的“纯粹空间”，这种空间是安藤思考人的本性的结果，是寻找建筑的物质性与人的使用性之间平衡的结果。所以在某种程度上，安藤忠雄的建筑表象就如同复杂的迷宫空间，这种表象是如画法则下的东方美学，隐藏其后的却是严谨的西方古典几何秩序。与路易斯·康柏拉图式的空间秩序相比，安藤试图将纯化的几何形体纳入复杂的迷幻路径，从而创造出多个矛盾节点，平衡进入建筑的人的复杂属性，他更多的是通过一个缓慢过程使得进入建筑的人逐步升华，这是一个动态的过程。而路易斯·康是通过对空间进行重组，将分离后的形体通过中心式的构成纳入到一个几何秩序当中，倾向于追求一种完美状态，是一个静态的过程。

1 阿尔巴斯的色彩构成

2 皮拉内西的《幻想的牢狱》

西方古典建筑无不充斥着人的理性，而当代社会人的属性是极具复杂性的。汲取了西方古典几何秩序把控手法的安藤忠雄也考虑到了人的理性与复杂性，他的建筑内部充满了理性主义的均质化，建筑外部却如人的属性一样充满复杂性，同时又有自然与之对立，所以安藤创作的建筑就成了一种平衡场所[2]。不同于西方的现代主义建筑大师，安藤因为生在东方，成长于西方，且未接受正统的建筑学教育，最终成为一位极具个性的建筑师。

2 起承转合：地中美术馆

在建筑的产生过程中，安藤通过旋转、重复或变化重复几何体块，建立理性主义均质化的场所空间。在地中美术馆的设计中，安藤将美术馆的建筑体量进行几何纯化，用一个方形和正三角形的庭院建立起与自然的对话空间，通过庭院空间衍生出一种几何秩序，在这种秩序之下不断旋转、重复变化庭院空间物化而来的方形几何体块，从而得出一组埋于地下的几何构架（图3）。方形和三角形的庭院成为整个构架的中心，庭院连接外界，引自然到地下，随着太阳的不断移动也产生丰富的光影变化，建筑就成了一个不断发生变化的、动态的空间[3]。安藤设计建筑天井及庭院的手法在很多作品中都有所体现，其中很大一部分原因是他早年在欧洲之行中受到了罗马万神庙的影响。

3 地中美术馆总平面图

2.1 几何生成

地中美术馆的几何生成逻辑并非是僵硬的几何形体加上规则的重复。我们将建筑形式几何纯化后，在地块的基础上置入a（正方形）、b（正三角形）两个几何形态，然后各自分别升起形成两个庭院空间（图4），通过庭院空间衍生出一种几何秩序，在这种秩序之下依据各自的边缘垂直方向，不断旋转、重复变化庭院空间物化而来的方形几何体块，依次生成矩形c、d、e、f（图5），接着加上附属的入口过道和连廊。不难发现，在地中美术馆的设计过程中安藤并没有用圆形来控制内部空间的尺度与几何形态，但是其几何空间内部却充斥着类似的几何秩序（图6）。同样，对地中美术馆的剖面进行几何分析，可以看出左右两个直径相等的圆决定了庭院的长、宽、高，体现了安藤对几何秩序的精确把握（图7）。

4 地中美术馆置入庭院空间

5 地中美术馆生成附属空间

地中美术馆可以物化成多个大小不一的几何形态（图8），虽然看起来都是简单的几何体，但进入其内部则是几何秩序下的多彩空间。地中美术馆从外部看似乎排列着若干个大小不等的房间，事实上内部的房间从尺寸到形状甚至采光形式都被赋予了几何秩序。在安藤对几何的掌控之下，每个几何体块的组成都存在着一定的几何秩序，或方或圆、或大或小、或咬合或衔接、或垂直或平行，这种把控是诸多因素影响下的结果。

6 地中美术馆几何秩序分析

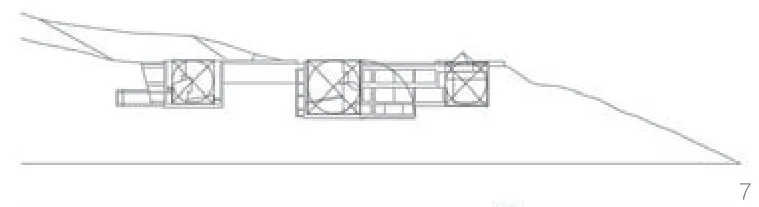
7 地中美术馆剖面几何解析

8 地中美术馆几何物化分析

2.2 路径生成

无论是帕拉帝奥运用砌块体系追求的完美轴对称结构的几何形态，还是柯布西耶将自己考证的多米诺体系完善成为可以构成自由平面、自由立面框架结构的几何形态，都影响着安藤的设计创作，使其一生都沉浸在西方均质化的理性主义当中。除此以外，安藤作为东方血统的建筑师继承了东方特有的一种园林文化——如画法则下的路径[4]。

安藤手下的路径极具特点，是几何秩序下的路径，也是抽象秩序物化后的具象迷宫。下文将重点分析地中美术馆的迷宫路径，阐释安藤忠雄的迷宫故事。首先，观众从入口a点进入一条走道，通过走道抵达地下空间部分，当走到尽头b点时，迎来第一个高潮——方形的庭院空间，这里是安藤建立的第一个与自然对话的场所，高高的围墙阻挡了观众的平行视野，能看到的只有天空，而且是方形的天空（图9）。原本复杂庞大的天空在这里瞬间纯化，经过高宽比一样的方块成为简单的一方天空，这是安藤置入几何秩序的结果。观众在这里开始思索，思索天、思索地、思索人，人类的复杂属性在这里也被瞬间纯化了，这或许就是安藤想要寻找的平衡。

9 地中美术馆方形庭院

继续往下走，沿着庭院四边的台阶上至c点，经过一个室内空间后继续向前，通过一道门瞬间调转方向来到接待大厅d点。安藤擅长运用这种迂回的路径，多是源于日本传统的回游园林、西欧如画法则以及安藤对于皮拉内西《幻想的牢狱》影响的思考。继续往前走，通过一道门洞口抵达e点，接着又进入一段冗长的过道来到终点f点，虽然看似已经来到了三角形庭院，但是观众依然看不到该庭院，直至走到g点掉转方向走出门洞，才能看到整个建筑的高潮——三角形的庭院空间。在这里观众似乎更加接近内心，建筑的物质性与人的使用性仿佛在此刻被三角形的庭院连接起来，我们猜想这应该就是安藤沉浸在西方均质化理性主义当中的结果。

继续向前走，沿着庭院楼梯下到h点，然后到达室内i点，接着又掉转方向回到庭院j点，最终顺理成章来到l点。上述路径完美演绎了如画的迂回法则。结束三角形庭院，从m点进入，便来到了室内的展厅空间。接着沿n点的坡道到达o点，左侧p点是另一展览空间。拐过一道门，往前走过一段黑暗空间，来到美术馆的最终展厅。最后，经过一系列复杂的迷宫路径，在位于r点的咖啡厅结束（图10）。

地中美术馆的路径设计融入了几何秩序（图11），每次路径的迂回转折不仅是方向、流线的掉转，还意味着秩序之间的转化——从一种几何秩序进入另一种几何秩序。整个建筑很好地诠释了安藤的迷宫故事，在其内部空间的体验中，“建筑几何学”所具有的普遍性以及与其相反的迷宫性、身体性的东西相互融合，并很好地在这个设计中体现出来。

10 地中美术馆路径分析

11 地中美术馆几何秩序下的路径分析

3 迷宫乐园：成羽町美术馆

日本回游式园林最早出现在17世纪，其特征是路径的百转迂回，虽然与中国古典园林的造园手法相似，但二者存在根本性的区别，日本对美的追求更倾向于其纯粹性及体验性。安藤作为东方血统的建筑师，对于东方的园林文化是内化于心的，这对于其迷宫性的建筑语言有一定影响。

安藤擅长把自己的作品与城市的喧嚣脱离开。在成羽町美术馆的设计中，他将进入建筑内部的人“封锁”在自己的建筑“迷宫”中，每个进入的人都必须走完这些充满了园林般“迂回”趣味的路线。这种在路径中引入抽象自然的做法作为一种叙事表达，将建筑从简单的几何体块转变成有生命力的盒子。安藤立足于东方与西方的交织点，思考着建筑的内与外、历史与现代、局部与整体、抽象与具象。游人在游览的过程中不难感受到，安藤思考的轨迹充斥着整座建筑（图12）。

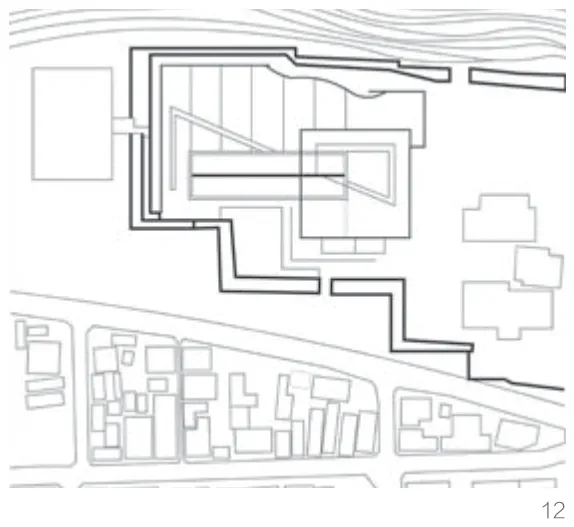
12 成羽町美术馆总平面图

3.1 几何生成

成羽町美术馆的几何生成逻辑首先是由一条直线生成一个矩形和三角形（图13）。矩形生成的功能是一个咖啡厅，也是入口的关键设计点，安藤在此处用一道片墙开始了成羽町的迷宫空间，利用他经常使用的三角形母题生成庭院空间，建立起与自然对立的场所。少量几何形体构成的片墙形式加上丰富的自然环境，使这里成为一处别具魅力的场所。

然后根据已有的矩形和三角形生成附属空间d、e、f，再沿着三角形长边方向生成三角形c（图14）。对于建筑与自然对立的问题，安藤有自己的思考。安藤对用地的解读及其对几何片墙的合理使用，使得加入的人工内容自然而突出，自然与人的关系更加丰富多彩（图15）。

与地中美术馆相似，成羽町美术馆的几何体块最终也可物化成多个不同尺寸的几何图形（图16），每个几何图形或大或小、或平行或垂直，各自有着几何秩序与几何空间，每个空间在相应的秩序下构成自己的一方天地（图17）。

13 成羽町美术馆置入庭院与咖啡厅

14 成羽町美术馆生成附属空间

15 成羽町美术馆片墙分析

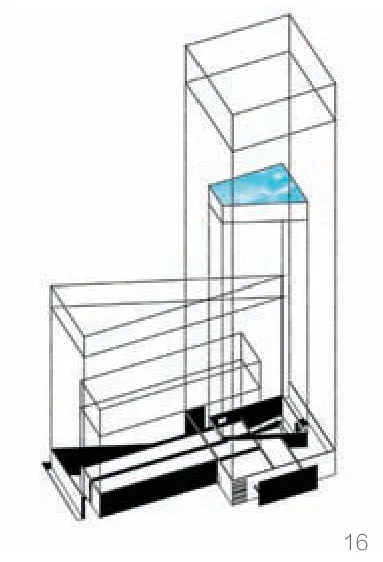
16 成羽町美术馆几何物化分析

17 成羽町美术馆几何秩序分析

同样，成羽町美术馆也有严格的比例关系，其斜向参观坡道与左侧的矩形对角线平行，而且这条对角线可以延伸至恰好通过正方体的一个顶角。主体部分为一个圆形控制下的方形空间，在展览空间与庭院空间（抽象与具象）之间寻求一种平衡，而这种平衡是通过一道斜墙来把控的。在此基础上，用一个大圆控制室外水池的空间尺度与从入口到展厅水平距离的平衡。在秩序之下引入复杂的迷宫路径，建筑的简单性与复杂性在安藤的作品中被完美体现。在这种环境下，人类的复杂属性逐渐被理性主义的均质所调和。

3.2 如画法则下的路径

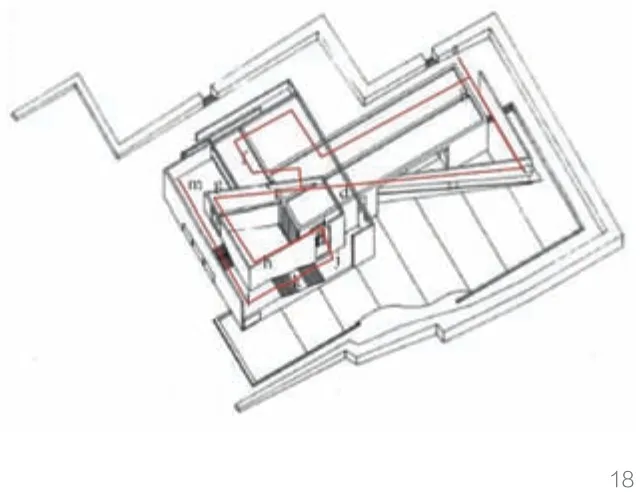
成羽町美术馆将如画法则下的迂回路径演绎得淋漓尽致。首先，参观者从入口a点进入，片墙分隔两边。顺着坡道而上，到达拐角处c点，继续往上行走，到达坡道尽头d点后正式到达二层。跟着安藤设定好的路线前进，通过过渡空间e点，往右可以进入f处的展厅，继续往前则到达美术馆的天井空间h点，穿过i点的门洞，顺着阶梯便可以到达m点的天台（图18）。

线条物化后的美术馆流线呈现Z字形，形象地展示了安藤在路径设计中采用的方向掉转手法。观众在沿Z字形迂回前进的过程中，与大自然和艺术文化有了接触。正如安藤所言，他想让这座美术馆成为文化和历史的交融场所，山峦与建筑之间的水面倒映出景色和建筑物，创造出一种虚拟的意向，观众可以同时看到虚无和真实，在这样的复杂情境下，建筑师其实是用户与建筑深层对话的中介，而实现对话的手段便是建筑师自身个性的表达。

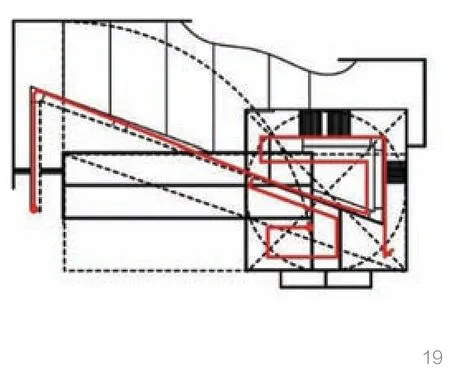
最后，将成羽町美术馆的Z字形的迷宫路径置入抽象化的几何秩序（图19），通过简洁的片墙，安藤建立起人与自然的对话空间，表现为对理性与自然的冲突、理性主义均质化与人复杂属性的调和，使观众在这座建筑中得到升华。

18 成羽町美术馆路径分析

19 成羽町美术馆几何秩序下的路径分析

4 结语

安藤作为东方血统的建筑师，迷宫性的建筑路径成为其个性表达，而帕拉帝奥所追求的轴对称结构的几何形态以及柯布西耶考证的多米诺体系的几何形态，又使得安藤迷宫的背后蕴藏着西方古典的几何秩序。随着路径的不断深入，让处于建筑中的人脱离自身及社会的复杂属性，不断升华，最终成为纯化后的人体几何。这便是安藤建立平衡场所的过程，也就是我们在讲的安藤的迷宫故事。