两阶段特征选择的冷水机组能耗预测方法

（1-华中科技大学中欧清洁与可再生能源学院，湖北武汉 430074；2-华中科技大学能源与动力工程学院，湖北武汉 430074）

0 引言

随着我国城镇化水平持续提高，公共建筑能耗总量呈不断上升趋势，并且在能源消耗总量中所占比例越来越高。据统计，公共建筑能耗已经达到总能耗 1/3以上[1]，其中中央空调能耗约占建筑能耗的50%[2-3]，中央空调系统节能优化对建筑整体节能影响重大[4-6]。冷水机组作为空调系统最主要的能耗设备，如何建立准确可靠的冷水机组能耗模型对冷水机组进行节能运行优化，成为该领域的研究热点之一[7-10]。冷水机组能耗预测模型主要包括机理模型和黑箱模型[9]。机理模型从冷水机组运行机理出发，通过辨识选取能耗模型参数，对机组性能进行研究，但由于冷水机组系统复杂，运行参数种类多且难以确定，难以运用到工程实践。针对冷水机组运行参数繁多这一特点，黑箱模型即基于数据挖掘的能耗预测模型，常采用特征降维算法来减少无关特征和互相关性较高的冗余特征，研究表明，基于特征降维算法的能耗预测模型能够有效地提高预测精度[11]。

目前，在冷水机组能耗预测模型的特征降维中，应用最为广泛和成熟的是主成分分析（Principal Component Analysis，PCA）方法[12-13]。PCA是一种基于特征变换的特征提取方法，原理是寻找使得样本散度最大的方向矢量，但由于PCA不考虑样本类别，提取出的低维特征空间难以解释，且对于回归预测而言不是最优的。ReliefF和最大相关最小冗余（minimal-Redundancy-Maximal-Relevance，mRMR）算法是两种特征选择降维算法。ReliefF算法通过计算各特征的权重，考虑特征与预测目标的相关性，能选出与目标相关性最高的最优特征，但由于其没有考虑到特征之间的相关性，特征间存在冗余，得到的特征子集也不是最优。mRMR算法考虑了特征间的相关性，但其选择的每维特征对预测的贡献均匀，体现不出对预测作用的差异[14]。

本文提出一种结合ReliefF和mRMR特征选择算法的冷水机组能耗预测模型。首先，利用ReliefF算法计算冷水机组各运行参数的特征权重，权重大小指示了其对预测结果的影响大小，选择权重大的特征作为候选特征子集。然后，利用 mRMR算法选择出与预测目标有最大相关性且特征间具有最小冗余性的特征子集，弥补 ReliefF算法不能去除特征间冗余的缺点[15]。

1 特征选择算法

特征选择是一种将原始特征集从高维降到低维的特征缩减方法，降维标准通常可以提高或保持精度，或者能够简化模型复杂性。当有d个特征时，可能的子集数有2d个，当特征维数很大时，不可能通过枚举的方式来获取到最优特征子集，因此，需要找到在合理时间内有效的方法。特征选择基于某种评估标准从原始特征集中选择最优特征子集，这些标准可分为过滤式方法和包装式方法[11]。

过滤式特征选择算法是利用评价函数计算特征变量对于预测目标的重要程度，然后通过设置阈值来移除对预测结果影响较小的特征，最终选择重要程度高的特征构成特征子集。过滤方法要将选择的最优特征传递给学习模型，如分类器、回归模型等。另一方面，包装方法需要将模型集成到特征子集搜索中，通过模型发现或生成并评估不同的特征子集，通过在模型上训练和测试特征子集来评估特征子集的适合度。因此，用于搜索特征集的最佳次优子集的算法实质上是“包裹”在模型周围。本文使用的两种特征选择算法中，ReliefF属于过滤式特征选择算法，而mRMR属于包裹式特征选择算法。

1.1 ReliefF特征选择算法

Relief算法最早由RENDELL[16]提出，最初仅局限于二分类问题的特征选择。Relief算法基于各个特征和类别的相关性为特征分配不同的权重，并将权重小于某个阈值的特征移除。由于Relief算法相对简单，运算效率高，结果令人满意，因此被广泛使用，但其局限性在于它只能处理两种类型的数据。因此，在1994年，KONONEILL[17]扩展了它并得到ReliefF算法，该算法可用于处理目标属性为连续值的回归问题。当处理多类型的问题时，ReliefF算法从训练样本集中随机抽取一个样本R，然后从R的同类样本集中找到R的k个近邻样本，从R的不同类样本集中找出k个近邻样本，最后更新每个特征的权重。

式中，diff(A,R1,R2)为样本R1和R2在特征A上的差；Hj表示同类k最近邻；Mj(C)为目标类别C(class(R))中第j个最近邻样本；m为迭代次数；p(C)为第C类目标的概率。

1.2 mRMR特征选择方法

mRMR特征选择算法是一种基于互信息理论的典型特征降维算法[18]。其主要思想是以互信息量为衡量标准，计算特征与特征、特征与目标的相关性，得到与目标具有最大相关性，且相互之间具有最小冗余性的特征子集。

给定两个随机变量x和y，它们之间的互信息定义[19]为式(2)：

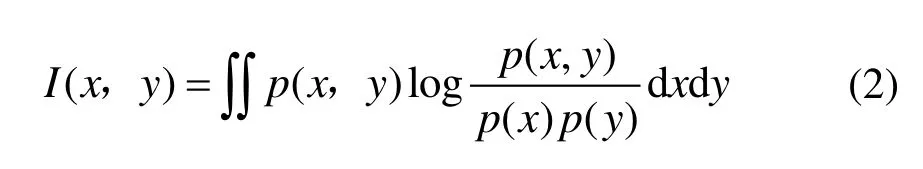
式中，p(x)、p(y)和p(x，y)分别为概率密度函数。特征与特征、特征与目标的互信息的计算定义如式(3)和式(4)所示：

式中，S为特征集合；c为目标类；I(xi,xj)为特征i与特征j之间的互信息；I(xi;c)为特征i和目标类别c之间的互信息。最小化特征子集S中特征的互相关度就是要最小化式(3)，最大化特征子集S中特征与目标的相关度就是要最大化式(4)。将式(3)和式(4)根据差准则进行组合，得到 mRMR的特征选择评估标准为max(D-R)。

依据此评估标准，采用序贯向前查找法依次选择最优特征。首先根据式(4)得到第一个与目标最相关的特征加入到特征空子集Sm中，当有m个特征被加入到Sm中后，根据式(5)在剩余特征集(S-Sm)中选择下一个特征加入到特征子集Sm中。重复以上步骤，直至得到期望数目的特征子集。

我们在清晨抵达TIT创意园。这里原来是诞生于1956年的广州纺织机械厂，如今遍布着酒店、咖啡馆、设计师工作室和生活方式集成店。按下启动按钮，捷豹经典的电子旋转换档控制系统从中控台缓缓升起，低沉雄厚的排气声浪在尚未苏醒的TIT响起。

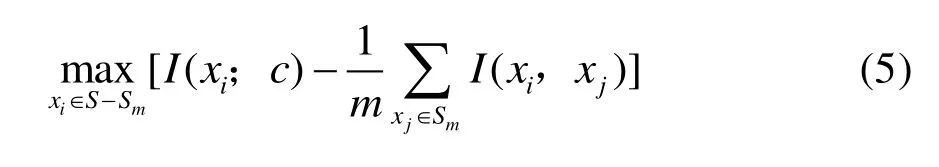
1.3 ReliefF-mRMR算法

ReliefF算法属于一种特征权重算法，省去了对特征子集的训练步骤，算法简单且运行效率高，但其不能去除冗余特征，预测准确度相对较低。mRMR算法利用学习模型对特征子集进行评价，基于互信息的评价标准能够去除冗余，预测准确率相对较高，但无法得到各特征的权重系数，体现不出不同特征对目标预测的差异性，并且 mRMR算法相对复杂，因此导致计算代价大，算法执行时间长。结合ReliefF和mRMR算法进行特征降维，可以得到对预测结果影响权重较大的特征子集，并利用mRMR算法对该特征子集去除冗余，既弥补了前者不能去冗余的缺点，也降低了后者的计算开销。

结合ReliefF和mRMR算法进行特征降维，可分为输入和输出两个步骤。

输入：原始数据集S、迭代次数m、最近邻样本数k和目标维数d。1）对样本S，用ReliefF算法计算出各特征与目标的特征权重，剔除权重较小的特征，得到一个候选特征子集S’；2）根据式(4)计算该子集S’中特征与目标的相关性度量；3）根据式(3)计算该子集中特征与特征之间的相关性度量；4）通过步骤 2的计算结果选择候选子集中与目标最相关的一个特征加入到最终的特征子集Sm中；5）依据 max(D-R)计算选择下一个特征加入到Sm中，直到选出d个特征为止。

输出：由d个特征组成的最优特征子集。

2 实验过程及数据采集

本文以某磁悬浮机组作为实验对象，冷水机组结构原理如图1所示。在压缩机、蒸发器、冷凝器等部位，设置传感器每0.5 min采集一次冷水机组运行数据参数，运行12 d共计34,491个数据，每个数据包含39个特征，部分运行数据特征如表1所示。

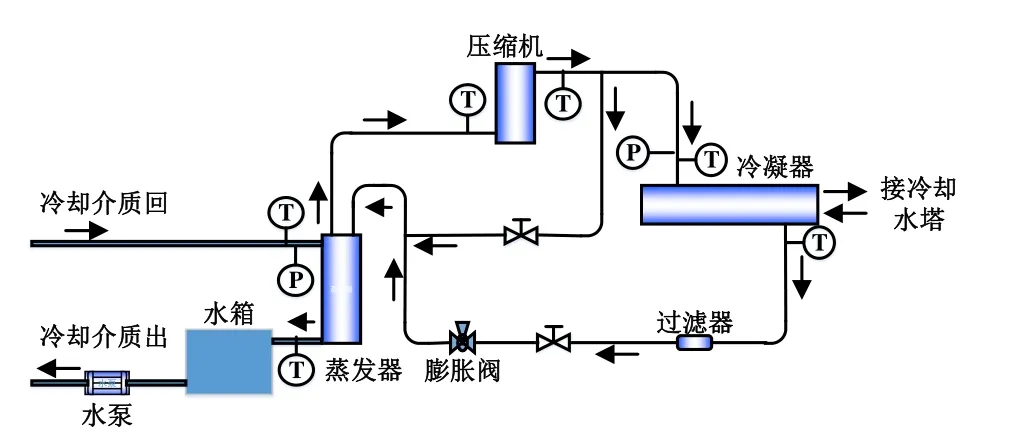
图1 冷水机组结构原理

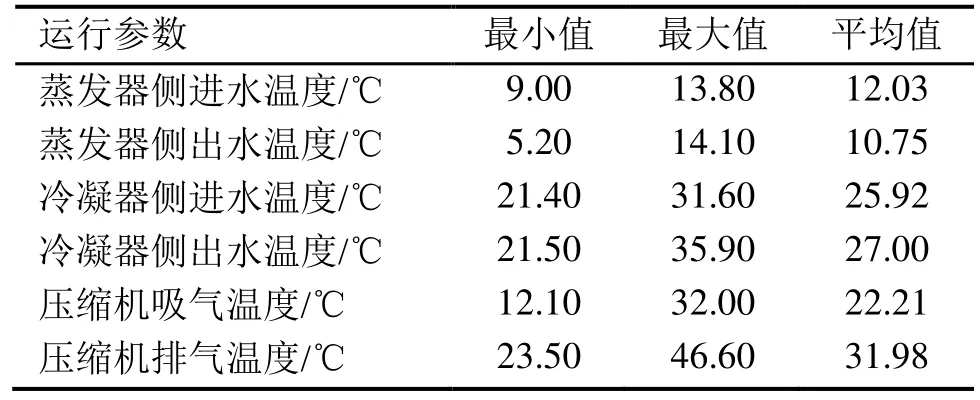
表1 运行参数

3 基于ReliefF-mRMR的能耗预测建模

本文以ReliefF-mRMR特征选择算法为基础，采用支持向量回归模型进行建模验证。具体建模过程包括数据预处理、ReliefF-mRMR特征选择、建立SVR模型和结果分析对比。

3.1 数据预处理

缺失值和异常值在数据收集过程中难以避免，如果直接将它们输入模型而不进行处理，分析结果的准确性将受到严重影响。因此，应首先分析数据，在初步数据探索之后，保证原始数据中没有异常值，才可以执行下一步的归一化过程。

由于输入数据中的不同特征具有不同的量纲和量纲单位，因此数量级差异通常很大，影响建模效果。归一化是一种简化计算的方法，它将有量纲的变量数据映射到[0，1]或[-1，1]区间，并转换为无量纲变量，便于不同单位或量级的变量进行比较和加权[20]。本文采用最小最大标准化方法对原始数据进行归一化，最小最大标准化方法公式如式(6)：

式中，maxF和minF分别为特征F的最大值和最小值；x为F的每一个原始值，x经过线性变换，被映射到值始终在[0，1]区间内的xnorm。

3.2 ReliefF-mRMR特征选择

利用 ReliefF算法处理最小最大标准化后的数据，得到各个特征与能耗数据的相关性权重排序，提取出权重系数较低的特征，得到特征维数为2d的候选特征子集作为mRMR算法的输入。利用mRMR算法去除候选特征子集的冗余，得到特征维数为d的最优特征子集。为了显示出ReliefF-mRMR特征选择算法的优越性和有效性，分别单独使用ReliefF算法和mRMR算法处理得到d维的特征子集，比较3种算法在不同特征维数d下的准确率来反映各算法的性能。将3种方法得到的特征子集划分成70%训练集和30%测试集作为SVR模型的输入，SVR模型参数均设置为默认值。

4 实验结果分析

本文选取R2(R-squared)作为模型评价指标：

图2所示为3种特征选择算法在不同特征维数d下预测精度的对比，表2所示为不同算法在预测精度最高时的特征维数和预测时间。由图2可知，ReliefF-mRMR特征选择算法在特征维数为8时达到最高的预测精度 0.956，而实验测得不使用特征降维算法的全特征预测模型的精度仅为0.867，ReliefF和mRMR单一预测最佳预测精度分别为0.935和0.948，预测精度得到一定的提高。并且对比使用单一特征选择算法，ReliefF-mRMR结合的特征选择算法在特征维数较低时的预测精度明显高于单一特征选择算法，而在维数较高时，3种算法的预测精度逐渐趋于一致。ReliefF-mRMR、ReiliefF和mRMR这3种算法1～18维特征平均预测精度分别为0.816、0.786和0.755，对比其他两种算法，ReliefF-mRMR算法的预测精度分别提高了3.92%和8.11%，均有一定程度的提高。

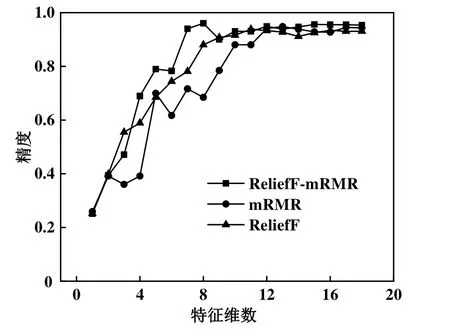
图2 预测精度与特征维数关系

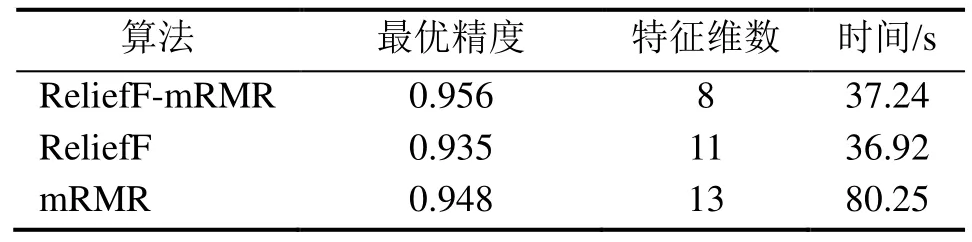
表2 最优精度下的特征维度和时间

从特征选择算法的效率而言，ReliefF-mRMR特征降维算法结合了ReliefF和mRMR两种算法的优势，在达到最优精度0.956下的特征维数仅为8，预测时间为37.24 s。与ReliefF算法相比，其预测时间基本相当，仅降低了0.87%，但维数和精度都得到了优化；与mRMR算法相比，其预测精度较为接近，但特征维数和预测时间大幅度降低。为了更好地显示ReliefF-mRMR算法预测效果，在测试集中随机选取了50个数据绘制了预测结果图，如图3所示。

由图3可知，预测值与真实值的绝对平均误差为81.42 kW，仅为选取数据平均值的2.40%，表明模型可以准确地预测冷水机组的能耗，可满足实际应用的需求。综上所述，RelifF-mRMR特征选择算法能够在较低的特征维数下达到较高的预测精度，并提高预测效率。

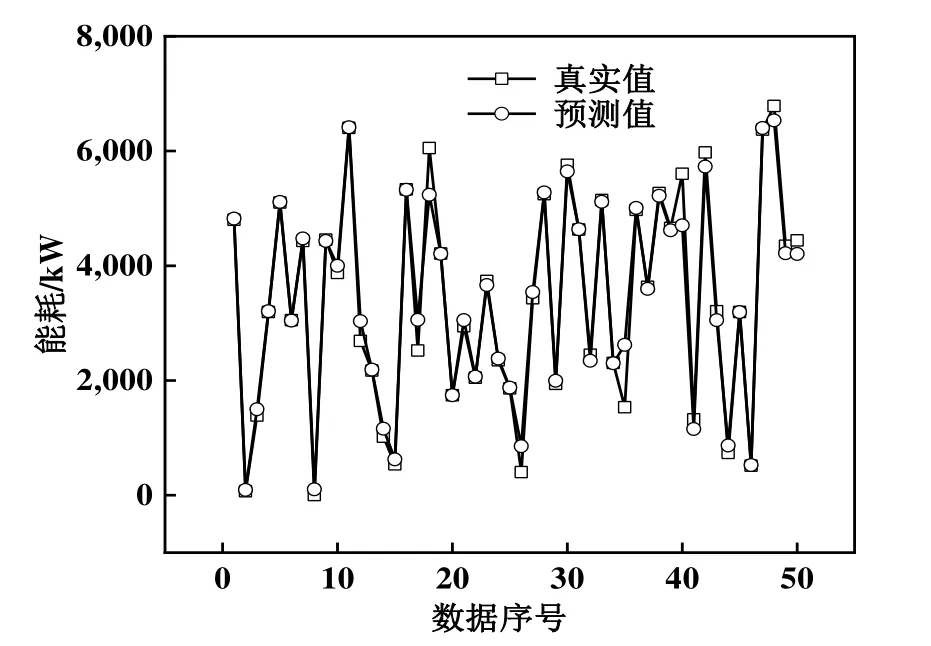
图3 ReliefF-mRMR算法模型预测效果

5 结论

本文将 ReliefF算法和最大相关最小冗余（mRMR）算法相结合，并应用于冷水机组能耗预测，介绍了算法原理以及建模过程，根据实验数据对算法进行了验证和对比，得出如下结论：

1）使用ReliefF-mRMR特征选择算法，建立的预测模型预测精度高达0.956，比单独使用ReliefF和mRMR算法的预测模型的最高精度分别提高了2.22%和0.83%；平均预测精度为0.816，比单独使用ReliefF算法和mRMR算法的预测模型的平均预测精度分别提高了3.92%和8.11%；

2）ReliefF-mRMR特征选择算法在保证精度的同时，能够提升预测效率。在最优精度的情况下，其预测效率与运行效率高的 ReliefF算法相比仅降低了0.87%，对比mRMR算法提高了53.60%；

3）Relief-mRMR算法能在较低的特征维数下保证预测精度和预测效率，能够减少冷水机组中传感器的数量，降低数据采集的成本。