基于遗传算法-误差反传神经网络的变风量空调系统空调箱故障诊断
2020-01-01张善兴何金凝杜志敏何军晋欣桥
张善兴,何金凝,杜志敏,何军,晋欣桥
(上海交通大学制冷与低温工程研究所,上海 200240)
0 引言
空调系统的高效运行,依赖于空调系统中各传感器、控制器和执行器的正常运行,如果没有精准的测量,很难完成设备的开发[1],如果没有高性能的控制,系统很难较快达到稳定状态[2]。当这些测控部件发生故障时,不仅造成空调系统能耗增加、室内热舒适性下降,还可能导致原有的优化控制策略紊乱、设备使用寿命减少、甚至运行事故等严重后果。因而针对空调系统传感器的故障检测和诊断已成为当前暖通空调领域的重要研究热点之一,不少学者对此进行了研究[3-5]。LEE等[6]提出了基于残差和参数辨识的方法,对空调系统风机和水阀故障进行诊断。CHEN等[7]建立了小波分析模型,对空调冷媒水系统中的传感器故障进行了诊断。YU等[8]提出了虚拟校准改进方法,应用于屋顶空调机组的容错和故障诊断。王世强等[9]提出了一种无中心算法,实现传感器故障检测。PADILLA等[10]基于主成分分析对空调箱内传感器故障进行了检测和隔离。误差反传神经网络因其非线性数据建模的特性,常用来对系统输入和输出之间复杂的关系进行建模,对于复杂HVAC系统故障检测和诊断有天然的适配性。LI等[11]基于神经网络预测正常运行参数,诊断复杂供热系统的故障。CASTILLA等[12]基于神经网络和多项式回归模型,提升了HVAC系统的热舒适性。WANG等[13]基于神经网络设计了一种针对变风量系统的故障检测方法,通过历史数据训练其中的神经网络后,可用于检测户外空气、进风、回风速率传感器的故障。
虽然BP神经网络有着较好的泛化能力,但其收敛精度一直是制约其发展的瓶颈之一[14]。通过梯度下降法作为学习法则,易使神经网络收敛于局部极值点,造成其精度下降。本文针对BP神经网络收敛精度低等缺陷,提出了基于GA-BP神经网络的变风量(Variable Air Volume,VAV)空调系统空调箱故障诊断模型,通过遗传算法优化BP神经网络的初始连接权值和阈值,避免神经网络收敛于局部极值点,提高了BP神经网络的训练精度,达到提高模型故障诊断准确率的目的。
1 研究对象
1.1 基于“硬件在环”的空调系统仿真控制实验台
故障检测策略的验证所需数据多数基于纯仿真平台,但由于纯仿真平台是由系统抽象出的数学模型,参数设定与实际系统不相符。混合仿真平台通过引入一定的实物设备,提高了仿真的精度[15-18]。因而经过混合仿真平台验证的故障诊断策略更具有实用价值。本文利用VAV空调系统混合仿真平台的运行数据来验证故障检测和诊断策略的有效性。
图1所示为空调系统混合仿真平台结构原理。该平台利用真实的PID控制器代替虚拟的控制器模型,不仅有助于提高系统仿真的精度,还有助于引进实物控制器在信号传输中所受到的干扰,缩小了与实际的建筑空调系统之间的差距。本文在该“硬件在环”实验平台上,通过仿真模型中的故障发生器,获取VAV空气处理单元的正常工况数据和相应的故障工况数据。
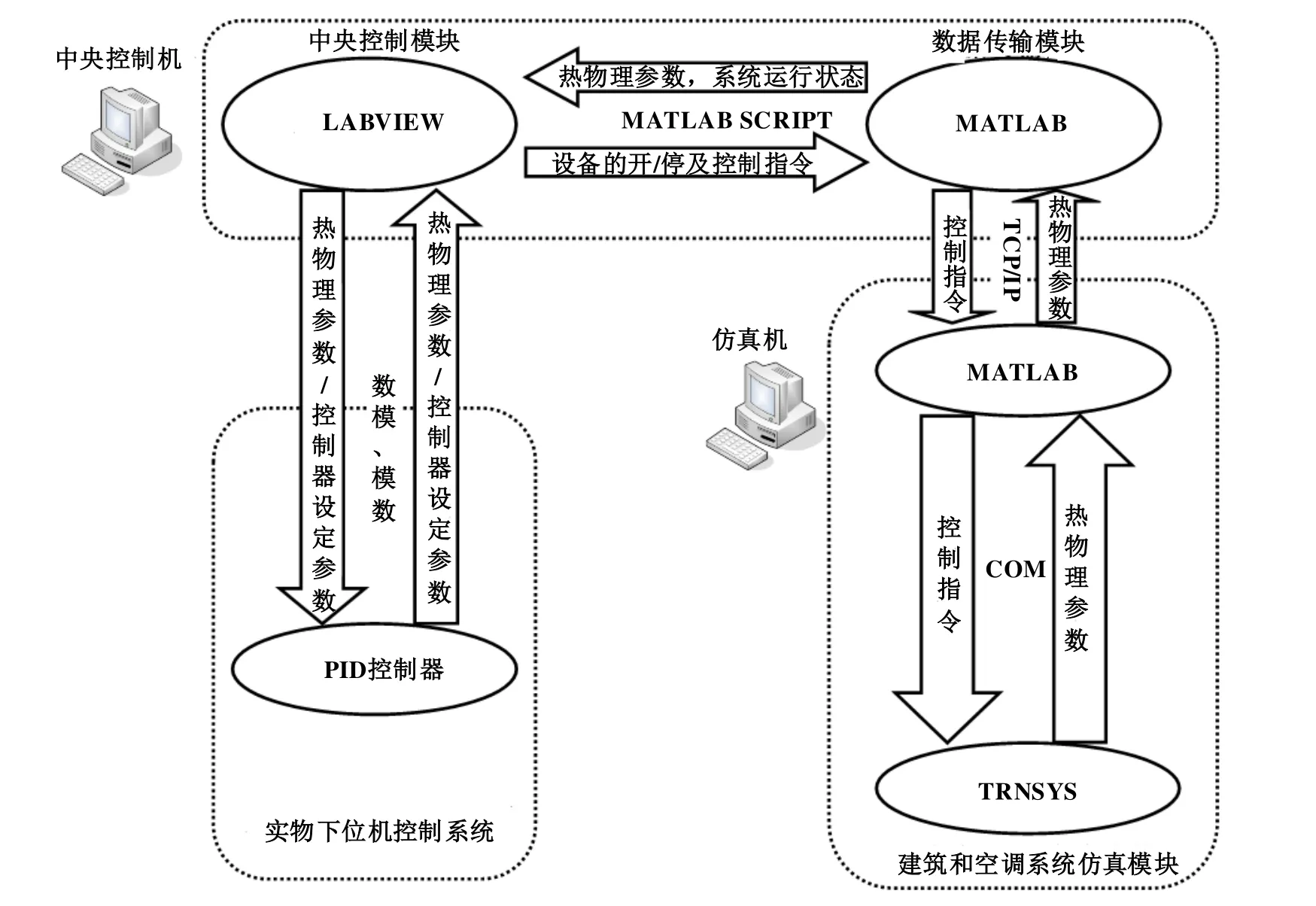
图1 空调系统混合仿真平台结构原理
1.2 研究系统
图2所示为VAV空调系统中风侧系统的结构[19]。通过接收送风温度传感器的温度值来控制空调箱中冷冻水水阀开度的大小,使送风温度达到温度设定值;VAV送风机则由一个送风静压控制器控制,通过改变送风机叶片的角度来维持送风静压稳定在设定值;回风风机叶片角度的调节则通过室内的正压控制器来调节;在VAV的末端通过流量控制器和温度控制器来改变VAV风阀的开度,使室内温度保持在设定值;以及利用新风温度控制器改变新风阀门、循环风风门以及排风风门的开度,达到调节新风风量的目的。
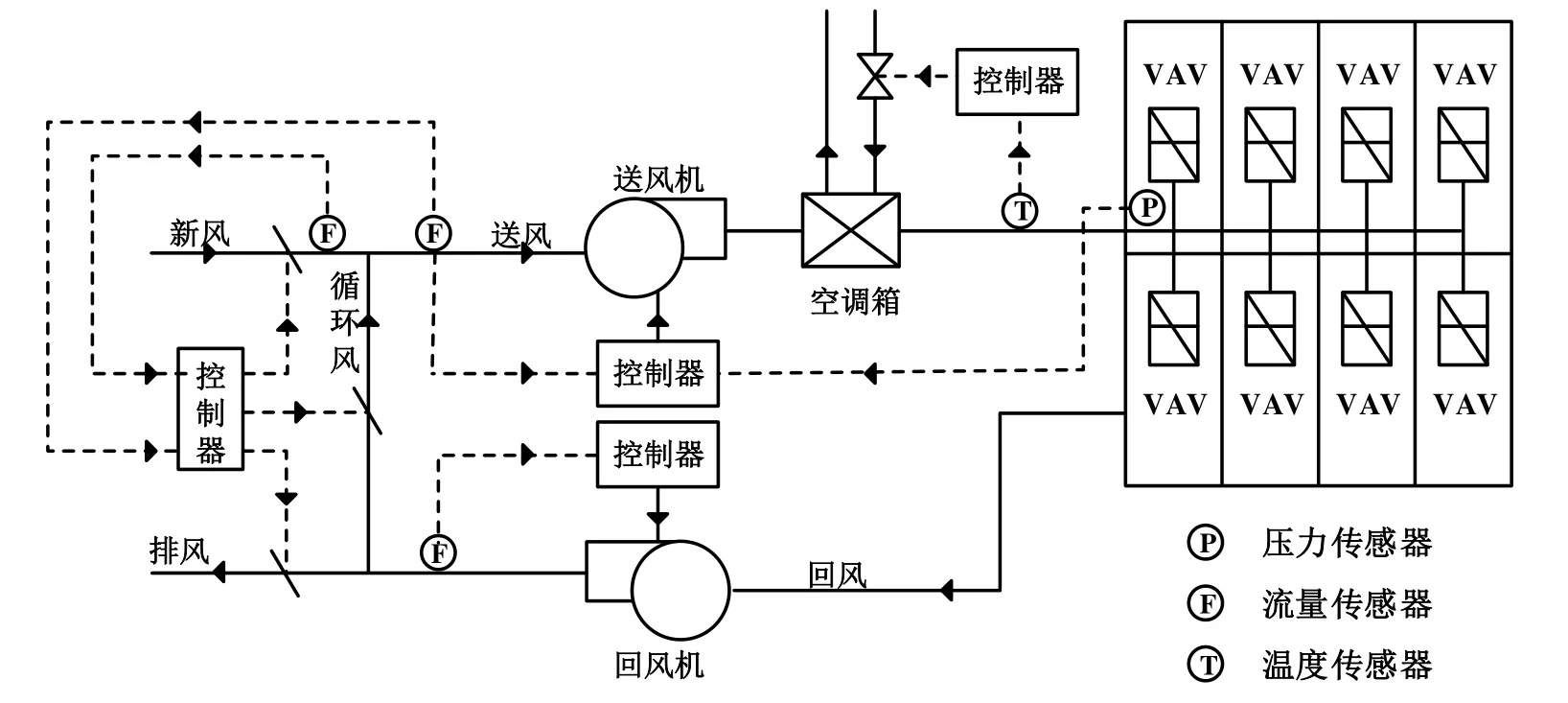
图2 VAV空调系统中风侧系统的结构
1.3 故障类型
本文研究的故障是空调箱内的相关故障。考虑到软故障是渐进性的故障,往往不易发现,为故障的检测带来一定的难度。因此根据故障特性将故障划分为6种软故障和2种硬故障[20],具体的故障类型和故障程度如表1所示。

表1 空调箱内相关故障
2 基于BP神经网络模型的故障诊断
2.1 BP神经网络
BP神经网络是应用最为广泛的人工神经网络,其本质是一种对于线性或者非线性系统进行黑箱建模的工具[21]。它是对人脑或者说是自然神经网络中相关特性的一种模拟,建立了多层感知器模型并以此感知外部的激励信号,在激励信号的正向传播出现误差时,通过反向调节的学习机制,不断进行迭代学习,构建出可以处理非线性关系的网络模型。其理论体系十分完善,算法流程也极为清晰,且具有良好的数据识别功能,这些都为非线性系统相关问题的解决带来了极大的帮助。
多隐层的BP神经网络原理与单隐层神经网络相似,结构如图3所示,包括了输入层、隐含层和输出层3部分。由于输入和输出向量具有确定的维度,因而输入层和输出层的神经元的个数也是确定的,只需对激励函数的类型进行选择。隐含层是神经网络中连接输入层和输出层的桥梁,神经网络的拟合精度受隐含层的层数、神经元个数和激励函数类型的影响。因此应合理地确定BP神经网络的结构,才能对空调系统的相关故障予以识别。
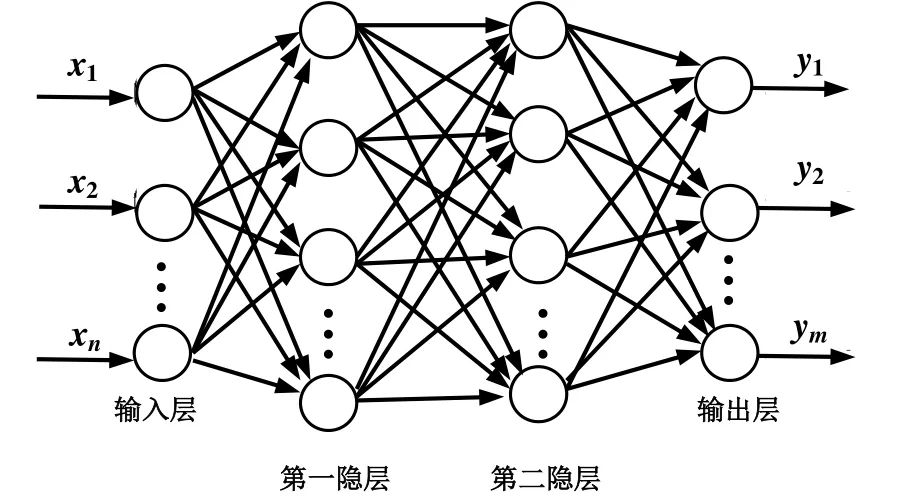
图3 多层BP神经网络的结构
训练网络时,首先赋予神经网络初始连接权值和初始阈值;再将训练数据集的输入向量带入至输入层,在隐含层的作用下求得网络的输出值,并与训练数据的实际输出进行对比,得到偏差E;利用梯度下降法的学习法则,对各个神经元的连接权值和阈值进行修正,直到偏差E收敛满足条件。当神经网络的收敛精度达到设定要求时,再利用验证集来验证其可靠性,若偏差不大则可将训练好的BP神经网络用于空调系统的故障诊断。BP神经网络的算法流程如图4所示。
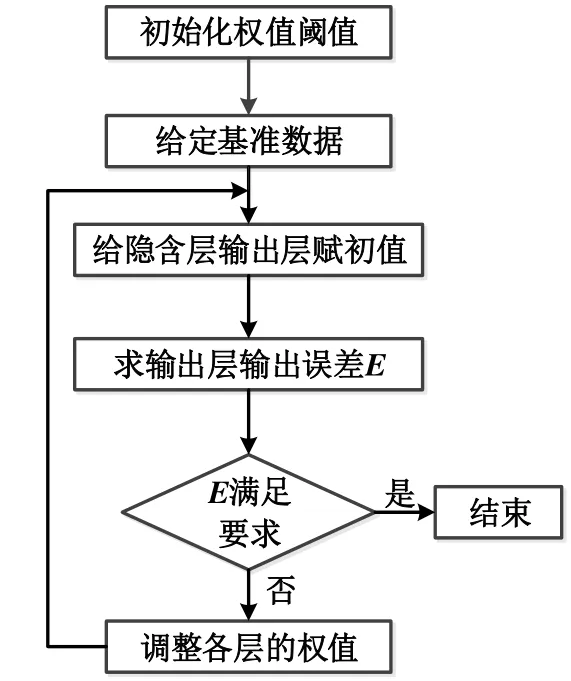
图4 BP神经网络算法流程
2.2 BP神经网络诊断策略
构建BP神经网络模型,需要大量的基准数据。在空调系统的实际运行中,某一参数的变化会引起其他相关参数的连锁变化,因而利用基准数据来训练网络,需要确定网络的特征输入变量。基于能量平衡的模型[3]可反映空调箱的运行状态和规律,选取新风温度Tfre、送风温度Tsup、回风温度Trtn、冷媒水供水温度Tws、冷媒水回水温度Twr、新风量Mfre、送风量Msup、回风量Mrtn、冷媒水供回水流量Mw、新风湿度dfre和回风湿度drtn这11个参数,作为BP神经网络的特征输入变量。由于各特征变量的评价标准不同,采取离差标准化进行归一化处理,利用线性函数将原始数据线性化为[0,1]范围内的数据。归一化公式:

式中:
Xnorm——归一化后的数据;
Xmax——样本数据中最大值;
Xmin——样本数据中最小值。
由基准数据及 11个特征输入变量,可以确定BP神经网络的输入矩阵和输出矩阵。以故障类型X=[x0,x1,x2,x3,x4,x5,x6,x7,x8]’所构成的矩阵作为网络的输入,其中x0、x1、x2、x3、x4、x5、x6、x7和x8分别表示在无故障和8种故障类型下包含 11个特征输入变量的数据矩阵。以目标输出Y=[y0,y1,y2,y3,y4,y5,y6,y7,y8]’作为神经网络的输出,若输出向量Y的第j行数值越接近1,则在8种故障中第j种故障类型的可能性越大,建立起故障类型与网络目标输出向量之间的映射关系,如表2所示。

表2 故障模式输入输出对应表
对于BP神经网络的隐含层结构,增加隐含层层数虽然可以减少隐含层神经元个数,但同时增加了网络的复杂程度及训练时间,因此本文选取3层(1个隐含层)的BP神经网络[22]。如果选取的隐含层神经元个数太少,网络所能获取的用以解决问题的信息量太少;而个数过多,训练时间增加,也会造成过度拟合使网络的学习能力下降。为了简化神经网络,建议适量减少隐含层神经元的个数,可正确反映输入输出关系即可。但在以往的研究中并没有固定的选择方法,一般由经验公式来确定隐含层神经元个数的范围:

式中:
N——隐含层所需的神经节点个数;
NI——输入变量的维数;
NO——输出变量的维数;
α——介于1~10之间的常数。
神经网络的输入层有11个输入神经元,代表11个特征变量的输入数据;输出层有9个神经元,对应于无故障和8种故障的判别输出结果。可以求得隐含层神经元个数取值为6~15。考虑到隐含层神经元个数对神经网络的精度影响较大,所以在此范围内设置其初始值为6,逐渐增加神经元个数进行训练,直到预测值与实际值输出间的误差不再大幅降低,通过不断的试验以获取最佳的隐含层神经元个数。隐含层神经元的激励函数选择tansig函数,则隐含层的第j个神经元的输入为:

式中,θi为神经元的阈值;vi为经阈值调整后的值。
最终的输出为:

式中,y(j)为最终的输出值。
确定神经网络的输入、输出以及结构后,可进行神经网络的训练和诊断。以前文所述的8种故障类型的数据作为网络的输入来训练网络,获得当前时刻的权值和阈值,判断实际值和目标值之间误差E是否满足设定条件。如果不满足,根据梯度下降法调节权值和阈值,直到训练网络能满足收敛条件。同样需要将待诊断的数据归一化处理,再进行诊断获取结果。误差E取神经网络的均方误差:
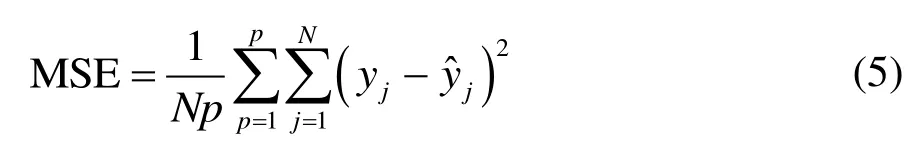
式中,N为神经节点数目;P为训练样本的阶数;yj为网络预测值;为网络实际输入值。
综上,BP神经网络模式识别模型的故障诊断流程如图5所示。
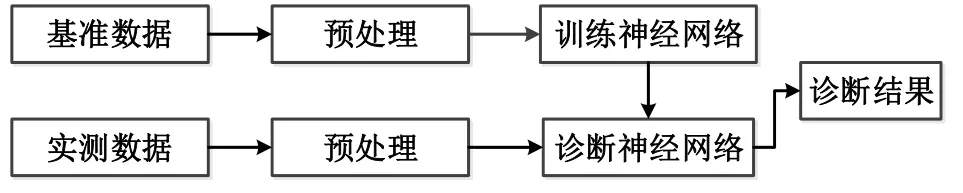
图5 BP神经网络模型的故障诊断流程
3 基于GA-BP优化模型的故障诊断
遗传算法是一种新的全局优化搜索算法,可很好地对BP神经网络的缺陷加以弥补,寻找全局最优解。遗传算法的流程如图6所示,包括编码、初始化种群、适应度计算、选择、交叉和变异等过程。
利用GA方法对BP神经网络的初始连接权值和阈值进行优化,解码获得最优的初始连接权值和阈值,再通过BP神经网络利用梯度下降法进行搜索,获得全局最优解。基于遗传算法优化BP神经网络模型的故障诊断流程如图7所示。

图6 遗传算法的流程
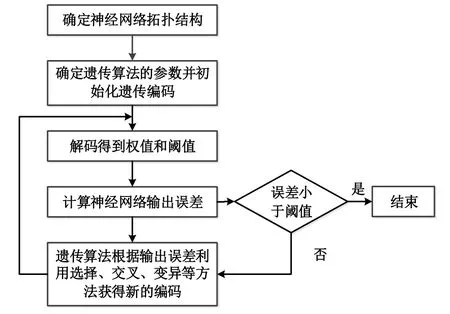
图7 GA-BP神经网络优化模型的故障诊断流程
4 实验验证
4.1 实验数据
通过“硬件在环”仿真平台获取了包含上述 8种故障工况和无故障工况的800组数据样本,对其进行归一化处理,并将相应的故障类型编号为0~8。将数据样本划分为650组训练样本和150组测试样本。利用训练样本分别训练GA-BP优化模型和BP神经网络模型,再将测试样本带入到训练好的模型中,进行故障诊断。
4.2 BP神经网络模型的故障诊断结果
图8所示为BP神经网络模型的故障诊断结果。由图8可知,在8种故障类型中,除了送风温度漂移故障的诊断效果较差,其余7种故障基本可以诊断出来,整体的故障诊断准确率为87.33%。
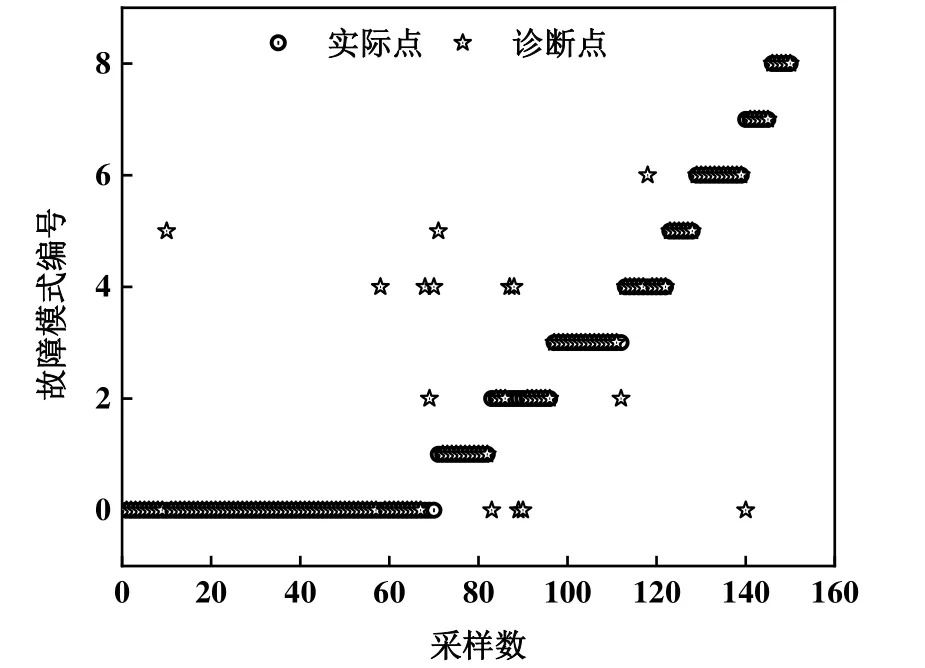
图8 BP神经网络模型的故障诊断结果
由于故障诊断结果的精度受到初始连接权值和初始阈值的影响,因而每次训练BP神经网络模型得到的诊断结果均不相同。当隐含层神经元个数为8~11时,取不同的初始连接权值和阈值,多次训练得到不同的BP神经网络模型,故障诊断的准确率如表3所示。由表3可知,在节点数相同的情况下,受初始连接权值和阈值的影响,BP神经网络每次训练得到的模型准确率存在较大差异。如神经元个数为8的BP神经网络模型的诊断准确率为66%~90.67%。
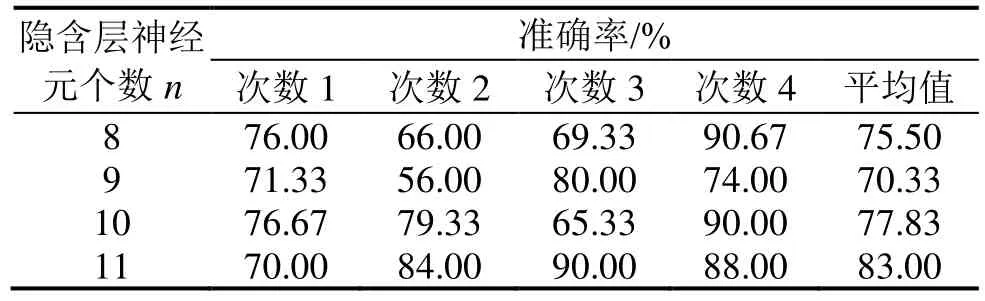
表3 BP神经网络模型故障诊断结果的准确率
4.3 GA-BP神经网络优化模型的故障诊断结果
图9所示为GA-BP神经网络优化模型的故障诊断结果。由图9可知,除送风温度传感器故障外,其余几种故障类型基本都可以判别出来,整体的故障诊断结果准确率为90.67%,优于BP神经网络模型的故障诊断结果。
考虑到故障诊断结果的精度受到初始连接权值和阈值的影响,对 GA-BP神经网络优化模型进行多次训练,结果如表4所示。由表4可知,以8个神经节点为例,各次训练得到的 GA-BP神经网络优化模型的诊断准确率为81.33%~86.00%,其模型精度受初始连接权值和阈值的影响较小,说明GA-BP神经网络优化模型的精度比BP神经网络模型更加稳定。
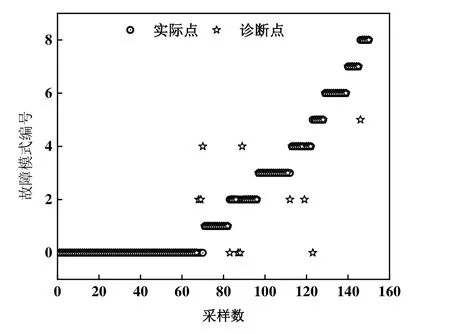
图9 GA-BP神经网络优化模型的故障诊断结果

表4 GA-BP神经网络优化模型故障诊断结果的准确率
图10所示为BP神经网络模型与GA-BP优化模型的诊断率随神经元个数的变化。由图10可知,GA-BP神经网络优化模型的故障诊断准确率整体高于BP神经网络模型;且GA-BP优化模型的故障诊断准确率随神经元个数的变化不大,而BP神经网络的故障诊断的准确率随着神经元个数n的变化波动较大。
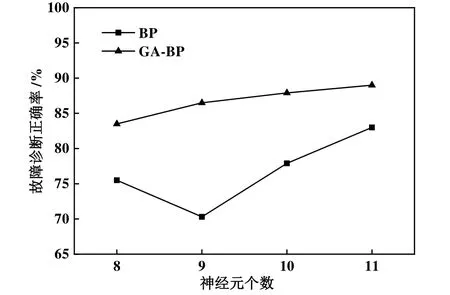
图10 BP模型与GA-BP模型的诊断率随神经元个数的变化
5 结论
本文针对BP神经网络存在易陷入局部最优解、训练精度低等问题,提出了基于GA-BP神经网络的故障诊断优化模型,对VAV空调箱的8种软、硬故障开展了故障诊断研究。并通过“硬件在环”空调系统仿真控制平台获取了正常工况和故障工况的数据,对比了上述两种模型,得到如下结论:
1)两种故障诊断模型对故障有很好的辨识功能,均可以用于VAV空调箱的软、硬故障诊断;
2)BP网络的初始连接权值和阈值的取值对模型影响较大,可以采用遗传算法对其进行优化。GA-BP神经网络优化模型的故障诊断准确率要高于BP神经网络的故障诊断的准确率;
3)当隐含层神经元个数在一定的范围内变化时,GA-BP神经网络优化模型的故障诊断准确率相对稳定且较高,而BP神经网络模型有较大波动;
4)当隐含层神经元个数相同时,在多次训练中,GA-BP神经网络优化模型的精度比BP神经网络模型更加稳定。
