一种振动颗粒康复仪的噪声分析与降噪设计*

2019-12-31曲云霞王世阳侯书军王梦迪

振动、测试与诊断 2019年6期

曲云霞，王世阳，侯书军，李慨，王梦迪

(河北工业大学机械工程学院天津，300131)

引言

人体上下肢的肌肉组织受到伤害后，皮肤容易对周围环境极度敏感，影响人体的正常功能[1]。如何让这些部位的肌肉神经组织尽快解除对所接触物质的过度敏感，是骨科手术后康复治疗的关键一环。在这类脱敏治疗仪器中，振动颗粒康复仪是本课题组开发的新型医疗康复仪器，其结构原理是：颗粒物容器在偏心振动电机的周期激励下做周期振动，通过容器内壁与颗粒、颗粒之间的相互冲击碰撞，使容器内的颗粒均处于振动流化状态。人体上下肢的受伤部位在进入振动流化的颗粒层后，即会接受相邻颗粒层的轻柔按摩，按摩的强度与方向可以通过步进电机来调节振动电机的激振方向进行控制，以获得更好的疗效。在振动按摩的过程中，该类装置会产生噪声，特别是低于300 Hz的中低频结构噪声。人体内脏易与频率范围3～50 Hz的低频和超低频噪声产生共振，导致内脏受到不可逆的损害；另外，长期在强噪声环境下工作会使人承受心理和生理的多重伤害，因此，对该类结构的噪声进行分析和有效控制，是该类医疗器械推广应用的前提之一。

本颗粒容器为一圆柱桶形薄壁结构，从振动噪声学的角度看，主要的噪声应来自颗粒容器的振动及其与颗粒碰撞后形成的高阶振动。贺晨等[2]利用有限元、边界元和统计能量分析方法建立了一套圆柱壳体在流场中振动声辐射效率在全频段的数值计算分析方法。白长青等[3]针对薄壁圆柱结构的研究发现声场在大多数情况下降低了结构的固有频率，在低频段声振动相当于增加了结构的质量，而在高频段声振动和结构阻尼的影响比较相似，空气声场对大多数模态固有频率值的影响相当于阻尼比为3%～6%的阻尼。Chen等[4]研究了复杂声学边界条件下圆柱壳结构的声辐射问题，为复杂声场边界声辐射问题的分析提供了一种新的方法。陈剑等[5]以挖掘机驾驶室为例，建立了结构有限元和声学边界元模型，将声学传递向量与边界元法相结合，计算了驾驶员右耳处的声压。目前，中低频段的结构辐射噪声的研究方法主要是有限元法和边界元法。在声场分析方面，有限元法对于结构内部的声场计算有优势，而边界元法对于结构外部的无界声场分析具有更高的计算效率[6]。研究人员建立了多种有限元与边界元相结合的数值分析方法来处理结构声学中的声辐射问题[7]。Junger等[8]使用分离变量法进行轴对称载荷作用下的球壳、无限长圆柱壳和薄板等简单结构的振动辐射与散射声场分析。Citarella等[9]基于试验和数值模拟方法，实现了预测噪声的排放及结构振源的相关性。程昊等[10]采用边界元法，推导了辐射声压关于频率、表面振速等设计变量的声学灵敏度公式。

振动颗粒康复仪的机械噪声由多种因素综合叠加而成，且各种噪声形成的机理各不相同[11]。笔者进行声强测试试验，通过数据分析，找到样机辐射噪声的主要来源，对主要发声部件建立有限元与声学边界元模型，根据有限元法得到模型结构的振动速度，输入声学边界元模型，分析得到了模型场点的声学响应。在考虑样机质量和经济成本的前提下，提出了优化结构、提高刚度、增加隔振的优化方案，计算金属材料和具有较大阻尼特性的材料场点处声压级并进行对比分析，最终优化方案有效降低了康复仪的噪声水平。通过场点处声强测试试验，验证了最终优化方案能够很好地抑制筒体振动、颗粒与筒体碰撞、筒体底部与振动平台的碰撞产生的噪声。

1 声强测试试验

1.1 噪声测试仪器及测试规范

测试平台采用LMS.Test.lab数据采集系统，其主要包括LMS SCADAS-SCR02数据采集器、G.R.A.S.50AI-L声强探头和数据处理模块，选用100mm的声强探头垫圈，声强探头频率测试范围为20～1 280Hz，动态范围为140dB。数据采集器通过LMS SCADAS-SCR02将时域信号放大，并经LMS Test.lab转换成频域，噪声信号测试系统如图1所示。噪声测试时根据振动强度大小和医院要求选取激振频率为32，36，40，44和48Hz作为典型工况，两振动电机均与水平面平行，分别测试典型工况下无圆柱桶、空桶和有颗粒时的噪声分布。

图1 噪声信号测试系统

1.2 试验测试点布置

样机噪声源识别试验测试点布置如下：采取近场声强测试法，声强测试网格平面与两电机轴线和圆柱桶轴线所形成的平面平行，声强测试网格平面距离桶壁外边缘20 cm，布置5×7的网格，网格边长为10 cm，分别测试每个网格中心处声强水平，测试点布置如图2所示。

图2 声强试验网格与测点布置(单位：cm)

2 试验数据分析

2.1 噪声源识别

通过近场声强测试法测得无圆柱桶、空桶和有颗粒时典型工况下的样机声功率级云图，分析发现各典型工况下有圆柱桶时有无颗粒最大辐射噪声均来自桶壁边缘位置。图3所示为激振频率为44Hz时的声功率级云图，通过比较图3(b)和(c)，发现噪声源主要集中在桶的中上部分，以桶的上边缘为主，振动电机、铝板以及传动系统产生的辐射噪声和圆柱桶相比并不明显。通过比较图3(a)和(b)，发现在用分部运转法去掉圆柱桶后，样机辐射噪声明显降低。表1所示为无圆柱桶、空桶和有颗粒时的声功率级，在各激振频率下，空桶时的声功率级相比无圆柱桶时增加了16.6～21.5 dB，有桶时有无颗粒声功率级相差在0.2～2.9 dB以内。因此，本样机的辐射噪声主要来源于桶壁和桶内颗粒的碰撞摩擦等。

图3 44 Hz有颗粒、空桶和无圆柱桶时的云图

表1 无圆柱桶、空桶与有颗粒时的声功率级对比

Tab.1 Sound power level of no cylindrical barrel, empty barrel and existing particles

激振频率/Hz无桶时声功率级/dB空桶时声功率级/dB有颗粒时声功率级/dB3265.086.588.43667.487.290.14070.888.690.74472.489.091.34875.195.795.9

2.2 噪声频谱分析

噪声频谱分析可以获得桶内颗粒、圆柱桶上壁边缘、圆柱桶底部边缘、两侧振动电机及齿轮传动系统等处的频谱特征，得到各噪声源的特征频谱峰值和频率范围，识别出噪声能量分布。

从对容器底部的振动加速度的频谱来看，除了主激振频率的成分外，还有很多的倍频成分存在。这说明振动电机的激振力是通过一个旋转轴系往上传递给支撑铝板，轴系的间隙碰撞应是倍频出现的主要因素。该类倍频激励在传递给薄壁容器后，即在容器上形成相应成分的振动，并形成噪声，如图4所示。从噪声功率的测试结果看，薄壁桶的引入使噪声功率增大20 dB左右。其中，前3次峰值频率均为44，174和217 Hz，分别为激振频率的1倍、4倍和5倍，比较突出，其余倍频处峰值声压级也不小。

在加入颗粒之后，颗粒与容器的碰撞带来以下作用：颗粒与桶壁的碰撞会进一步引发倍频；颗粒与桶壁的碰撞也会消耗能量，从而起到减振作用。主频及其8，10，11，12，13次倍频峰值均有不同程度的减小，特别是表1中声功率随激振频率增大至48 Hz接近桶的基频时，有无颗粒的声功率几乎不变，因为此时颗粒碰撞的阻尼作用凸显，见图5。

总的来讲，颗粒的引入一般会使空桶振动的各阶峰值减小，同时又在各峰值周围引起相近频率噪声，总的声功率贡献与桶自身振动对声功率贡献相比要小很多。

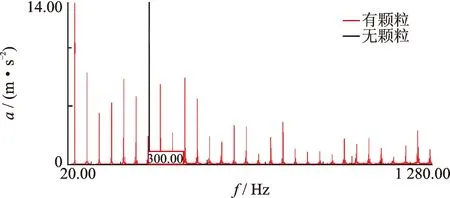
图4 44 Hz时振动加速度频谱图

图5 44 Hz激振下有桶与有无颗粒时的声压级频谱对比

3 结构与声学模型

建立准确的有限元模型是取得可靠分析结果的前提。笔者将主要发声部件圆柱桶的简化三维模型导入Hypermesh中，进行有限元网格的划分、约束等前处理。在处理时忽略工艺孔、过渡圆角及多余卷边等对圆柱桶结构影响很小的工艺结构，以提高有限元网格的质量和计算精度。将处理好的模型导入Virtual.Lab进行振动响应分析及声辐射计算，得到振动的位移、速度幅值，并将声学响应试验和有限元模型计算结果相对比，以证明所建有限元模型的有效性。

3.1 结构有限元模型建立

所建物理模型仅考虑圆柱桶、底板、支座和复合弹簧，其中复合弹簧的压缩变形量很小，可忽略其非线性问题。对应有限元模型如图6所示，各零件的材料属性如表2所示，有限元分析各项参数如表3所示。由于越低阶的模态有效质量越大而越容易被

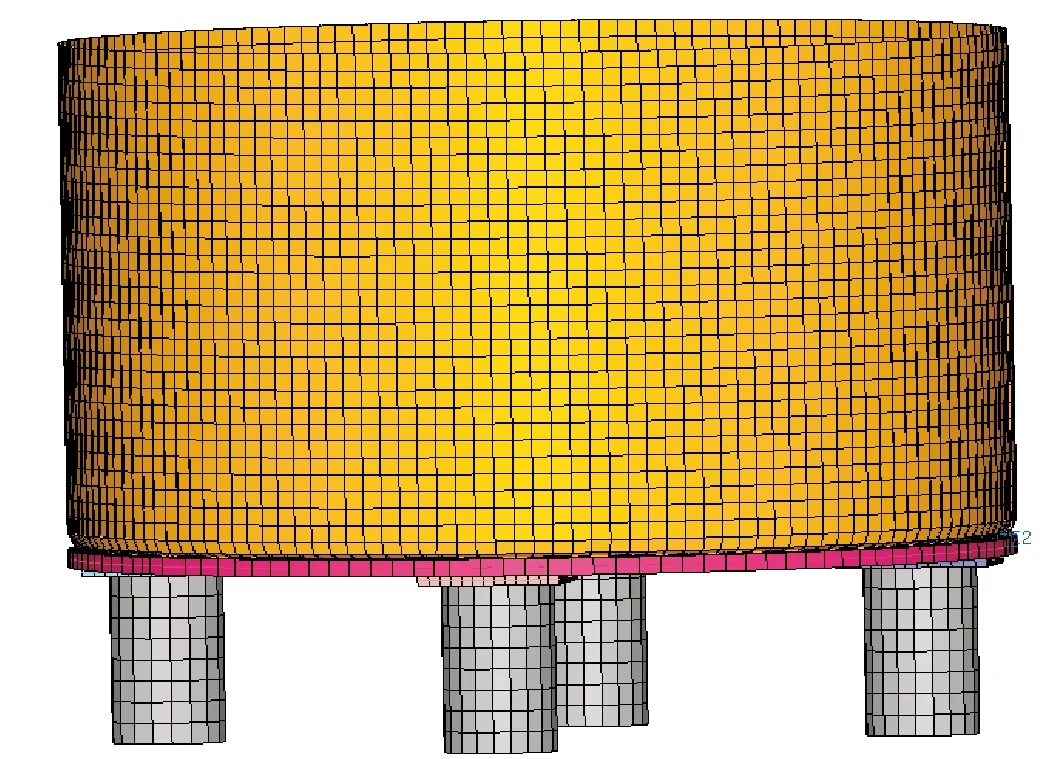
图6 圆柱桶简化模型

表2 各零件的材料属性

Tab.2 Material properties of each part

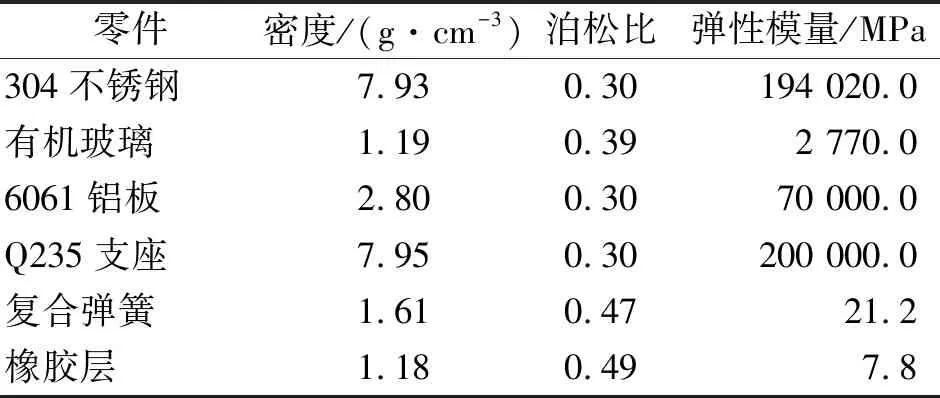
零件密度/(g·cm-3)泊松比弹性模量/MPa304不锈钢有机玻璃6061铝板Q235支座复合弹簧橡胶层 7.931.192.807.951.611.180.300.390.300.300.470.49194 020.02 770.070 000.0200 000.021.27.8

表3 样机模型有限元分析的各项参数

Tab.3 Prototype finite element analysis of the various parameters

零件材料厚度/mm网格单元尺寸/mm节点数单元数圆柱桶底板支座弹簧304不锈钢6061铝合金Q235橡胶110610068868 0982 4888623 4658 0052 3957602 464

外界激振力激发，因此，笔者基于Block Lanczos方法，计算得到有限元模型的前4阶非零模态频率。采用锤击法对模型进行模态试验，前4阶非零计算和试验固有频率如表4所示。两种方法得到的固有频率存在一定误差，但误差在工程允许的范围内。

表4 圆柱桶前4阶固有频率

Tab.4 The first four natural frequencies of cylindrical barrel

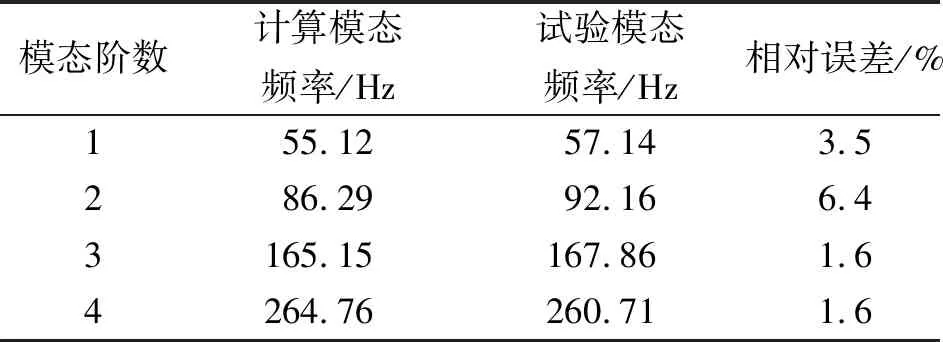
模态阶数计算模态频率/Hz试验模态频率/Hz相对误差/%1 55.12 57.143.52 86.29 92.166.43165.15167.861.64264.76260.711.6

3.2 声学边界元模型建立

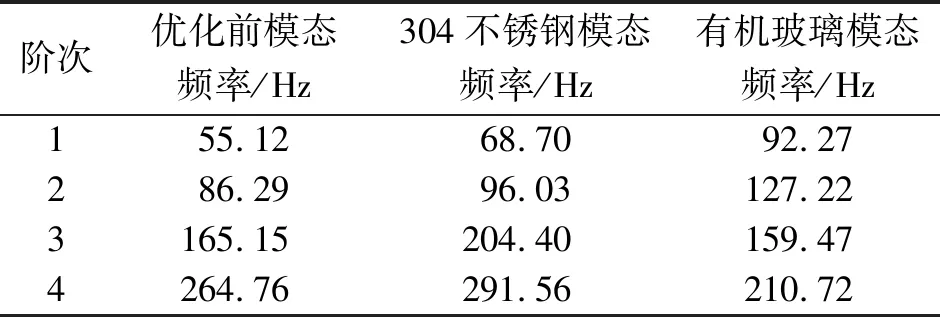
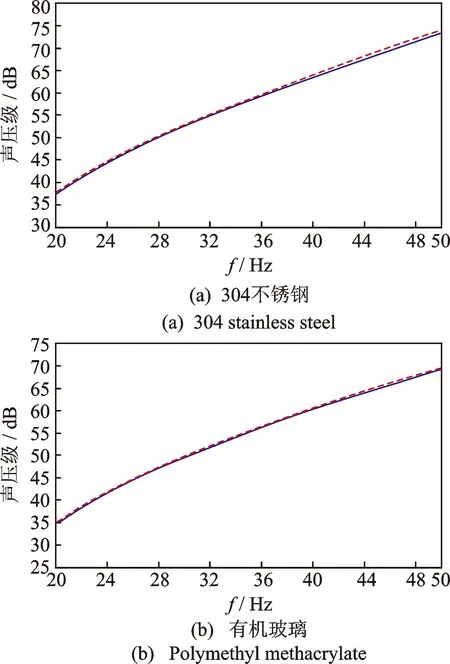
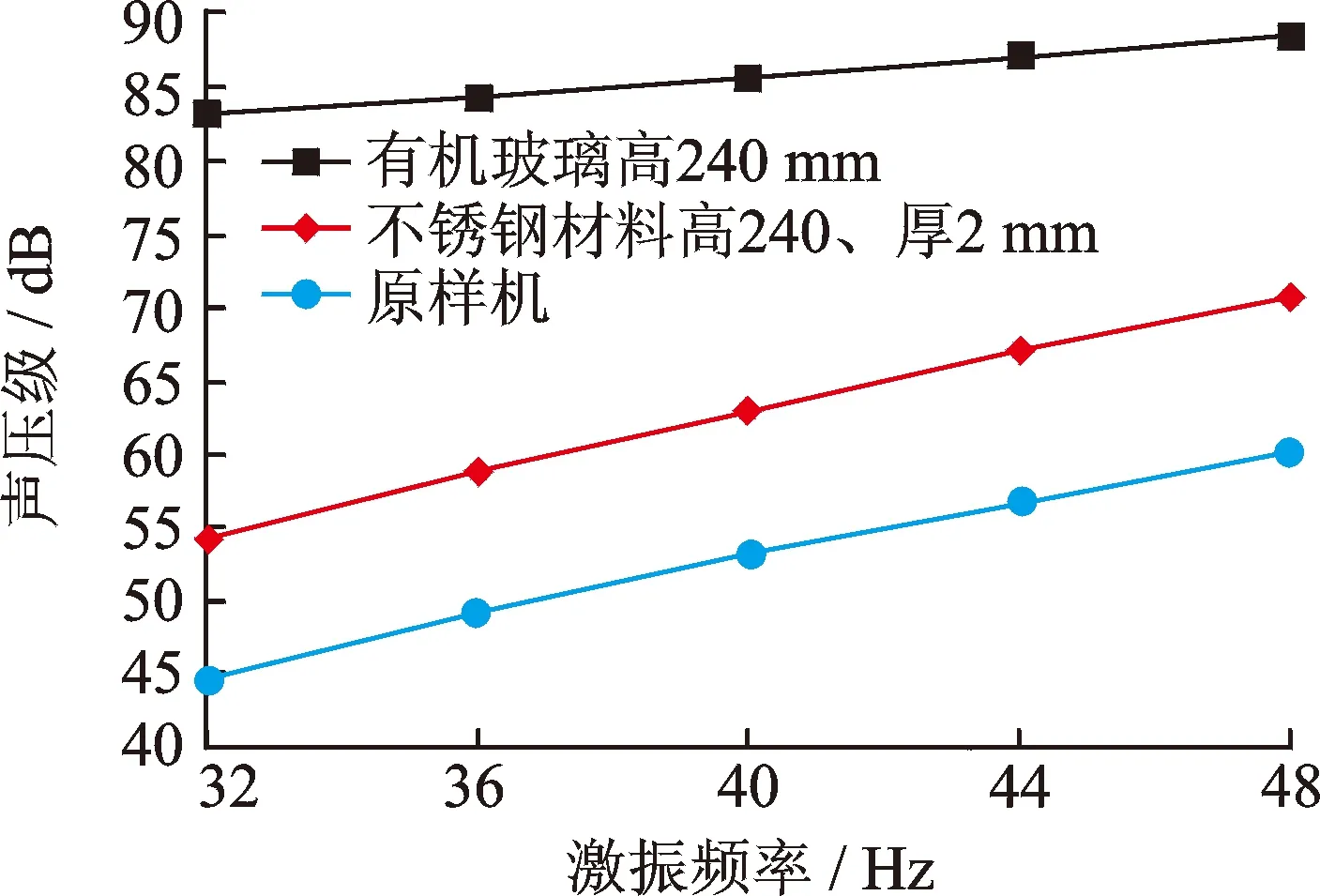
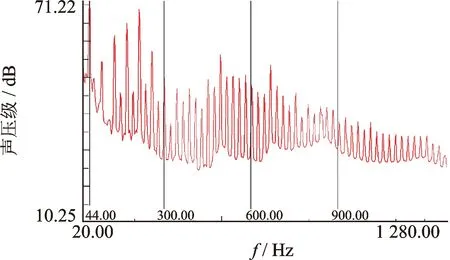
笔者采用声学间接边界元法计算圆柱壳体外声场[11]，在进行LMS Virtual.Lab Acoustics分析时，考虑了反射、衍射和折射等效应。为减小计算结果的误差，应保证在最小波长内有6个单元，即需要的长度L应满足L

图7 声学边界元模型

4 振动响应与声学响应

4.1 振动响应分析

本研究的样机有两个相同的激励源，且激励载荷相同，激励载荷通过桶下铝板传递给圆柱桶，使桶壁振动，产生辐射噪声。考虑到激励载荷提取的精度和复杂程度，笔者只考虑竖直方向的正弦激励载荷对圆柱桶的激励作用。

样机的复合弹簧之上质量为40 kg，其中复合弹簧之上的简化模型部分质量为8 kg。额定转速(3 kr/min)下单个振动电机产生的激振力为1 kN，因此额定转速下简化模型所受的激振力为200 N。由公式ω=2πN/60，代入F=meω2，可得到各激振频率下产生的正弦激振力的最大值，如表5所示。有限元模型在各典型工况下振动速度云图相似，图8所示为激振频率为44 Hz时的振动速度云图。

表5 各激振频率的激振力幅值

Tab.5 Amplitude of excitation force at each excitation frequency

激振频率/Hz323640444850最大激振力/N80.8103.0126.2152.7181.8200.0

4.2 噪声传递函数分析

4.2.1 分析方法

本模型先进行结构的模态分析，然后用模态叠加法进行模态响应分析[12]。本模型的结构有限元方程式为

(1)

其中：Mss和Kss分别为模型结构的质量矩阵和刚度矩阵；Fs为施加于结构的外力矢量；u为结构位移矢量。

本模型的声学包络网格方程为

(2)

其中：Mff和Kff分别为模型声学包络网格系统的声学质量矩阵和声学刚度矩阵；Ff为各单元表面传给流体的广义矢量；P为各节点的声压矢量。

考虑模型结构与空气之间的相互作用，声固耦合系统的有限元方程式可以写成

(3)

其中：S为模型的结构声学耦合矩阵；ρ0为空气密度；c0为声波在媒质中传播的速度。

最后把场点的空气压力转化为场点的声压值

(4)

其中：Ppre为参考声压。

4.2.2 基于结构模态的场点频率响应函数计算

噪声水平评价试验的测试点布置如图9所示。为模拟患者使用本样机进行治疗时的声压级水平，在人耳位置布置声强探头，测得样机在无颗粒时典型工况下工作的声压级。分别定义患者左右耳为两场点位置，模拟试验样机激振力位置定义激励。首先，计算模型约束状态下0～500 Hz内的结构模态；其次，用模态叠加法得到两场点处的声压级频率响应函数曲线，如图10所示。将取得的计算数据和无颗粒时的测试结果进行比较，发现计算与测试声压级趋势相同，且测试和计算结果相差均在3 dB以内，如图11所示。计算与测试间存在一定误差，其原因主要有以下几点：a.试验样机模型过于复杂，计算所用模型进行了简化，只研究了主要噪声源圆柱桶及铝板，而没有考虑一些次要噪声源；b.试验提取激励力时存在一定的误差，在分析时只考虑了竖直方向主要载荷的作用而忽略了水平的次要载荷，且两振动电机的激励力大小存在一些差别；c.计算值只包含圆柱桶壁和铝板振动引起的结构噪声，而测试声压包含结构噪声和空气噪声；d.在计算场点声压时添加的各阶结构模态阻尼比与实际阻尼比存在一定的偏差。但是，从噪声的测试与分析结果随激振频率的变化规律来看，一致性很好，因此可以认为该计算模型能够满足后续分析优化的精度要求。

图9 噪声水平评价试验的测试点布置

图10 场点处声压级频率响应曲线

图11 测试和计算情况下声压级对比

5 主要噪声源的控制与优化

欲降低圆柱桶的声辐射，最可行的办法就是抑制圆柱桶的振动幅值。为此，可从提高圆柱桶自身的刚度入手，以减小其振动响应的幅值；或考虑在圆柱桶底部增加弹性衬垫，以便对圆柱桶进行有效隔振。如图12所示，从原来的封底结构变为法兰，通过1层4mm厚的橡胶垫圈与铝板相连，组成振动颗粒按摩容器。圆柱桶选用304不锈钢和具有较大阻尼特性的有机玻璃材料，分别进行声学计算及对比分析。设置的场点与测试试验模拟的人耳处场点相同。笔者用Hypermesh进行有限元前处理，Virtual.Lab进行模态分析和计算场点基于结构模态的噪声传递函数，采用的优化模型的有限元网格如图13所示。

图12 优化方案剖视图

图13 优化模型的有限元网格

考虑实际应用工况，笔者所选桶高均为240 mm，304不锈钢材料时壁厚为2 mm，有机玻璃材料壁厚为5 mm。

对优化方案进行模态分析，并进行优化前后对比，部分模态频率如表6所示。由表6可见，优化后模型的模态频率得到提高，圆柱桶的刚度得到增大，且优化方案的第1阶固有频率均大于50 Hz，特别是有机玻璃材质，第1阶的固有频率有效避开了共振区，可降低圆柱桶的振动，减小声辐射。

表6 简化模型优化前后部分模态频率

Tab.6 Partial modal frequency before and after simplified model optimization

阶次优化前模态频率/Hz304不锈钢模态频率/Hz有机玻璃模态频率/Hz155.1268.7092.272 86.2996.03127.223165.15204.40159.474264.76291.56210.72

图14所示为计算得到两种材料下的场点处基于结构模态的声压级频率响应曲线，图15为两种优化方案与原样机模型声压级对比图，由图可知，笔者提出的结构优化方案能很好地降低场点处的声压级。具有较大阻尼特性的有机玻璃材料比304不锈钢更能抑制辐射噪声的产生，如在激振频率32 Hz时，两种材料声压级相差9.4 dB；激振频率48 Hz时，声压级相差10.5 dB。与原样机各典型工况下声压级对比，有机玻璃材料的优化方案能大幅度降低声压级。从质量角度考虑，原样机模型质量为13.5 kg，不锈钢模型为13.75 kg，有机玻璃模型为9.94 kg，与原样机模型相比质量降低了26%；从成本角度考虑，有机玻璃加工价格大约是304不锈钢材料的一半，可见有机玻璃材料优势明显。

图14 优化方案场点处声压级频率响应曲线

图15 两种材料优化方案与原样机模型声压级对比图

6 试验验证

根据最终优化方案对样机加工安装，进行场点处声强测试试验，验证优化方案的合理性。各工况下的频谱规律相同，在此均以激振频率44 Hz的声压级频谱为例作说明。图16为激振频率为44 Hz无颗粒时的声压级频谱，峰值声压级均在激振频率处产生，且各倍频处声压级峰值均很小，可见优化方案可以很好地降低因桶体底部与铝板碰撞产生的倍频处噪声和筒体因振动产生的辐射噪声。300 Hz以后出现较低峰值的倍频噪声，这是由于轴承箱体以及锥齿轮等碰撞产生的。图17为激振频率44 Hz有颗粒时的声压级频谱，由图可知，前5阶倍频峰值均较大，且整个频谱波谷相较于无颗粒均有较大提高，和优化前有颗粒频谱规律一致，说明这些倍频噪声以及较大波谷均是由于颗粒的碰撞摩擦产生的。图18为各工况下优化前后声压级A级计权对比图，当空桶时，优化方案最大降低了15.2 dB(A)；当有颗粒时，最大降低了3.5 dB(A)，因此，有关筒体的优化方案是合理的。