采用鱼群算法进化极限学习机的假肢步态识别*
2019-12-31陈增强刘作军
刘 磊, 陈增强, 杨 鹏, 刘作军
(1. 郑州轻工业大学建筑环境工程学院 郑州,450002)
(2. 南开大学人工智能学院 天津,300350)
(3. 河北工业大学人工智能与数据科学学院 天津,300130)
引 言
随着交通事故、工伤、自然灾害等意外伤害的发生,假肢的研究越来越受到重视。中川昭夫等研究了气动式摆动相控制膝关节[1]。英国的Blatchford公司和德国的 Otto Bock公司先后研制出了可以自动识别有限路况的智能仿生假肢[2]。冰岛的Ossur公司推出新款智能仿生膝关节 RHEO KNEE 3[3]。大阪大学采用磁流变阻尼器设计踝关节假肢[4-7]。近年来,国内也有越来越多的大学和研究相继开发了智能假肢[8-11]。
要想对假肢进行灵活控制,必须准确识别残疾人的步态。目前常用的步态识别信号源有角度、加速度、表面肌电信号(surface electromyography ,简称sEMG)等信息。由角度、加速度传感器等组成的物理传感器网络不仅会使假肢穿戴者感觉累赘,还会由于人体运动与反映意图的神经冲动之间存在自然的电-机延时现象,致使假肢步态的识别存在滞后。在步态识别研究中,视频信号和sEMG都有着较为广泛的应用,sEMG相比于视频信号获取方式更为直接,其采集方式更加适用于智能假肢装置,因此笔者将sEMG作为控制信号源实现假肢步态识别。现有的基于sEMG假肢步态识别方法,首先采集受试者sEMG信号,提取sEMG的绝对值积分、过零次数、中值频率及小波(包)变换系数等时域、频域、时频域特征,然后采用支持向量机(support vector machine, 简称SVM) 、ELM和线性判别分析(linear discriminate analysis,简称LDA)等分类算法识别出不同的步态。文献[9]研究结果表明,ELM方法识别率要优于SVM和LDA等方法,但是ELM正则化参数在一定数值范围内的微小变化会影响ELM分类精度。上面在sEMG数据处理过程中仅考虑了通道和时间2个维度的信息,张量分解方法能够有效地分析时域、频域及空域等多维信息。为了从空间、频率、时间及任务等多维度描述肌电信号,笔者从sEMG信号的张量数据中提取特征,寻找投影矩阵,以获取特征值。分类器的设计是步态识别关键环节之一,为了克服ELM方法中正则化参数在一定范围内的变化会影响ELM识别准确率的缺点,笔者对特征值选取核函数进行空间映射,利用FA优化ELM参数,最后利用FA-ELM识别步态并与粒子群算法(particle swarm optimization,简称PSO)优化的ELM进行对比,实验结果表明,张量投影矩阵能有效表征平地行走、上楼、下楼、上坡及下坡的特征,鱼群算法优化极限学习机方法对于假肢步态识别有良好的准确性,优于SVM和ELM等方法。
1 实验方法
1.1 基于张量投影特征的表面肌电信号特征表示
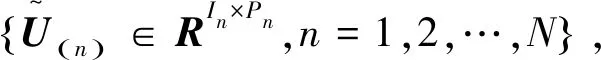
(1)
其中:×表示张量乘积;⊗表示克罗内克积;Yj∈RP1⊗RP2⊗…⊗RPN,j=1,2,…,M。

令Xj(n)表示第j个样本的n模式矩阵,则
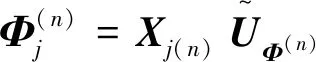
(2)
(3)

(4)

(5)
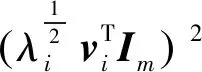
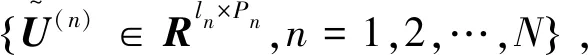
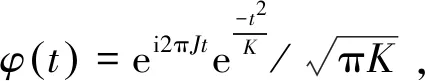
(6)
其中:J为中心频率;K为带宽参数。
笔者经过高斯小波变换建立了一个 4阶张量。sEMG数据具有通道×时间×任务三维结构,经过高斯小波变换后构建的张量数据具有通道×频率×时间×任务4维结构。
1.2 鱼群算法进化极限学习机
极限学习机可以看作是单隐含层网络,内部为全连接。其中输入层、隐含层和输出层的神经元数目分别为n,l和m,如图1所示。ELM将神经网络训练过程简化为矩阵求逆问题,学习速度明显提高。
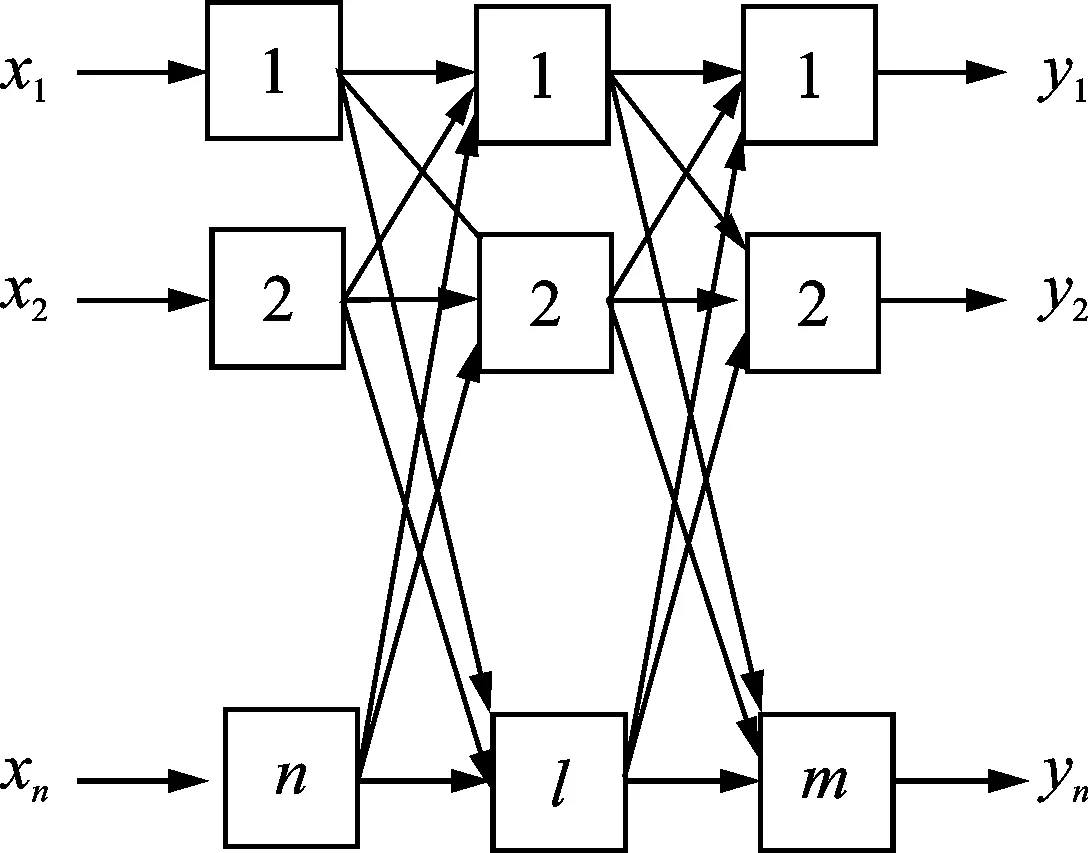
图1 极限学习机网络结构
笔者采用鱼群算法优化ELM参数。图2 为鱼群算法中人工鱼的视野和移动步长示意图,表示人工鱼当前位置,其视点在某一时刻停留的位置为Xv,若该位置Xv的食物浓度高于当前位置X的浓度,则人工鱼向食物方向前进一步到达Xn; 反之则搜索其他方向的食物。
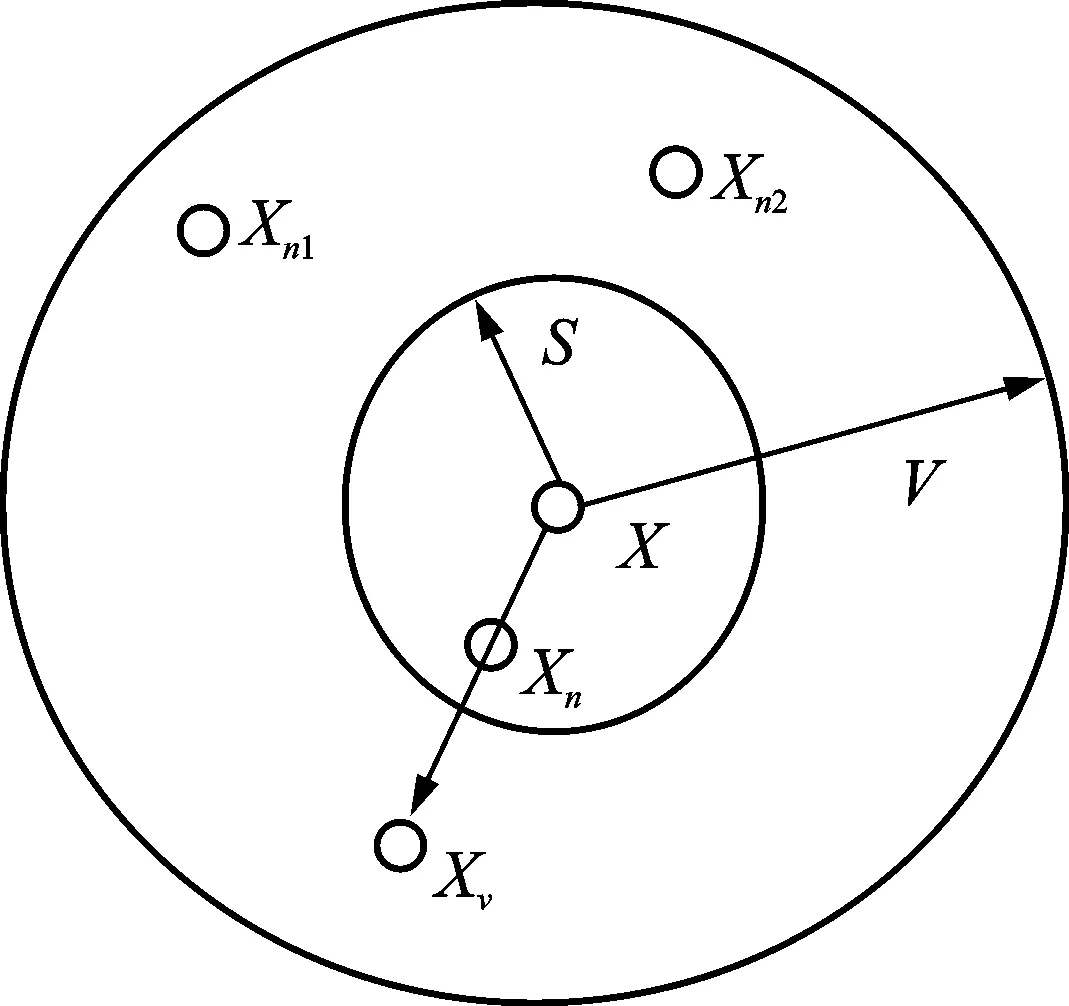
图2 人工鱼的视野和移动步长
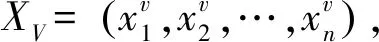
(7)
(8)
其中:r为[-1.1]之间的随机数;S为移动步长;xi为人工鱼初始位置;Xn为人工鱼移动后的位置。
由于环境里的其他人工鱼数目是有限的,因此人工鱼改变自身位置的方法仍与式(8)相同。
2 下肢假肢步态识别实验
2.1 实验方案
实验过程中,10位大腿截肢患者参与了本研究的步态识别实验,其中男性大腿截肢患者6名,女性大腿截肢患者4名,基本资料如表1所示。楼梯有10级台阶,台阶高度为广泛应用的 150mm;斜坡是无障碍通道的10°斜坡;平地实验在宽阔的室外走廊中进行。使用美国Noraxon公司的MyoTrace400采集sEMG,该设备可以同时采集 8 块肌肉的肌电信号。笔者参考文献[12-14]选择股直肌、缝匠肌、阔筋膜张肌、半膜肌、半腱肌和大收肌为表面肌电信号采集肌肉群。实验前,受试者残肢端的体毛剔除,不能做剧烈运动。每位受试者采集平地行走、上楼、下楼、上坡、下坡5种步态的表面肌电信号各100组,共采集了100×5×10组数据。2 500组作为训练集,2 500组作为测试集。为了消除步速差异对步态识别的影响,每位受试者速度均匀地行走。笔者采用文献[12]的方法确定每路肌电的起始点。在实时处理表面肌电信号的过程中,Abel等[15]已证明最合适的窗口大小为150~300ms。笔者采用300ms小段数据进行特征值提取和步态识别。
大腿截肢者穿戴被动式假肢在平地行走时健肢侧与假肢侧能够实现交替运动,在上、下楼梯与上、下坡时不能实现健肢侧与假肢侧的交替运动。上楼梯与上斜坡均为健肢先运动然后假肢跟随运动,健肢保证在残肢前方;下楼梯与斜坡假肢保持在健肢前方,假肢先运动,健肢快步跟上。本实验中平地行走、下楼、下坡先迈残肢;上坡、上楼先迈健肢。肌电信号的幅值作为肌肉收缩力的间接反映,两者并非一一映射关系,需要建立不同实验对象和步态的参考标准。为了克服该问题,通常选择参考值进行归一化处理。常用的方法是选择最大自主收缩值作为肌肉收缩的参考[16],消除实验条件的影响,将测试值由毫伏值转化为所选参考值的百分数,如图3所示。幅值归一化处理并不是改变sEMG曲线的形状,只是改变y轴的缩放比例。时间归一是在单步周期内选取均布的300个离散点,将连续的肌电信号变成1个1维数组,进而利用同等动作条件下的多个有效单步周期进行平均,得到该步态的单步肌电模型。

图3 归一化分析后的sEMG

表1 受试者情况统计表
2.2 步态特征提取与降维
(9)
在 sEMG的张量表示中,中心频率J和带宽参数K是影响识别结果的重要参数,笔者采用10折交叉验证方法来选取J和K。利用ELM分类器分类识别,将J和K分别取[-10,10],对不同(2J,2K)组合分别训练ELM,识别率最高的一个组合为最优J和K。2J的取值为(2-10,2-9,…,29,210),2K的取值为(2-10,2-9,…,29,210)。图4中,当2J=2,2K=0.5时得到的识别准确率最高。
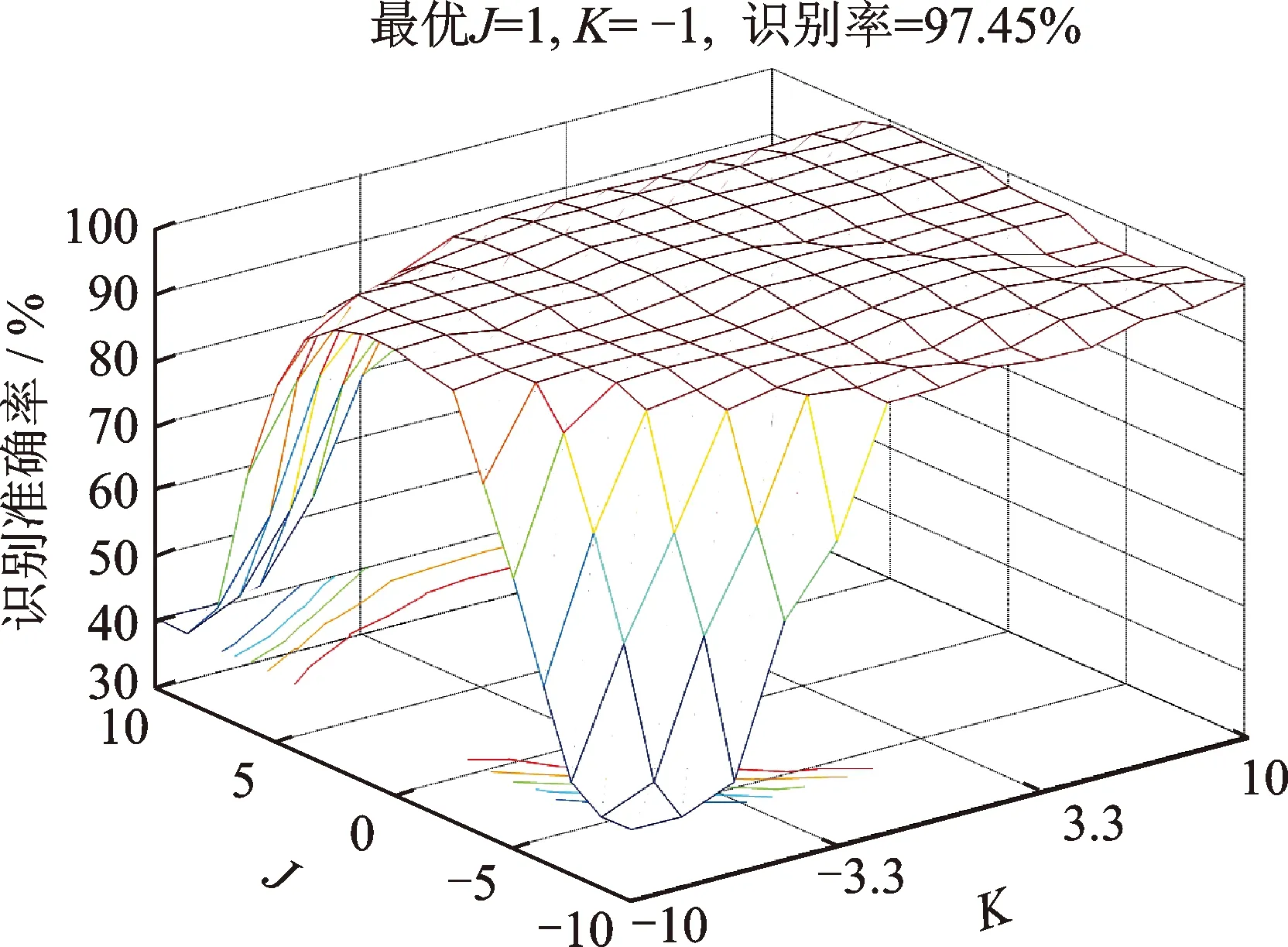
图4 中心频率J和带宽参数K的选择结果
sEMG原始数据为6×300×180(通道×时间×任务),经过高斯小波变换后成4阶张量,即6×12×50×180(通道×频率×时间×任务),3个投影矩阵分别为U6×3,U18×9和U100×16。数据投影和矩阵化后,每一个任务的特征维数为Z=3×9×16=432,原始数据对应的特征维数Z=6×300=1 800。与原始数据相比,张量特征的维数已经缩小很多。
张量特征的维数较高, 如果直接作为分类器的输入向量,将导致训练过于复杂,因此还需要对特征值进行降维。主成分分析(principal component analysis,简称PCA)是一种降维的有效方法,其基本思想是选取主成分累计贡献率大于95%的前N列主成分。实验表明,取前36主成分时,累计贡献率可达96.27%。
2.3 不同特征值比较分析
sEMG的特征提取通常有时域法、频域法、时频域法等。常用的时域特征有均方根(A1)、肌电积分值(A2)、绝对均值(A3)、过零率(A4)、斜率符号变化数(A5)和波长(A6)。时域方法计算量小,运算复杂度不高。常用的频域特征包括峰值频率(A7)、平均功率频率(A8)等。常用的时频特征值有小波变换系数、小波系数绝对值最大值(A10)等。
为了说明本研究特征提取的有效性,采用SVM 作为模式分类器对提取的特征进行分类,采用径向基核函数作为SVM的核函数。图5给出了采用不同的单一特征时的平均识别准确率和方差对比,可见肌电信号的大部分时域特征和频域特征识别准确率较低。由图5可以看出,在所有的特征提取算法中,张量特征(A9)表现出最好的分类准确率,张量特征方法识别率最高,稳定性最好,其代表性、分离度更好。这是因为张量特征能够从时间、空间、频率等多个模态上提取肌电信号的有效信息,因此,笔者选用张量特征作为步态模式识别的特征值。

图5 采用不同单一特征时的平均识别准确率和方差对比
笔者采用戴维斯和唐纳德指数(davies-bouldlin index,简称DBI)来评价sEMG特征的区分度。DBI 的值越小,特征的区分度越好。不同特征值的 DBI 值如图 6所示。由图 6看出,采用张量特征提取方法DBI最小,明显优于其他特征提取方法。

图 6 采用不同特征时的 DBI 指标对比
2.4 不同ELM参数优化方法比较
分类器的设计是步态识别最后一个环节。ELM参数确定的过程相对简单,核函数参数Q和正则化参数C是影响识别结果的重要参数。多次实验后,笔者选择小波核函数的ELM分类器,因此采用小波核函数设计ELM分类器,利用鱼群寻优算法得到最优C和Q。极限学习机的正则化参数C搜索范围设置为(0,120),小波核函数参数Q的搜索范围设置为(0,80)。AF中的参数进行初始化设置:最大迭代次数为100,V=3.2,S=0.6。笔者将分类过程中的10折交叉验证识别率作为网格搜索法、PSO 及FA的适应度函数。式(10)为适应度函数,K=10,xir与xiw为第i次测试集中正确和错误识别的样本数目。用二进制计数方式对5种步态定义:平地行走为(1,0,0,0,0);上楼为(0,1,0,0,0);下楼为(0,0,1,0,0);上坡为(0,0,0,1,0);下坡为(0,0,0,0,1)。识别准确率是衡量识别效果的重要参数,定义如下
(10)
图7为正则化参数C和ELM核函数参数Q的优化过程,最终得到最优解C=112.60,Q=75.48。笔者采用文献[17]提出的PSO优化方法确定PSO参数。由表2可以看出:网格搜索优化方法5种步态的识别率在82.51%~89.17%之间,平均识别率为85.64%;而采用PSO优化后,除了下楼,其余步态的识别率均在90%以上,平均识别率达到了92.8%,但仍低于FA参数优化方法识别率;FA参数优化方法比PSO参数优化方法平均识别率提高了4.6%;网格法只对经验范围进行寻优,是一种局部寻优算法,所以识别率最低。FA参数优化方法能够更准确、更有效地找到正则化参数和ELM 核参数的优化组合值,因此笔者采用FA优化ELM的分类方法。
表2 不同ELM参数优化方法识别准确率
Tab.2 Different ELM identification accuracy parameter optimization method%
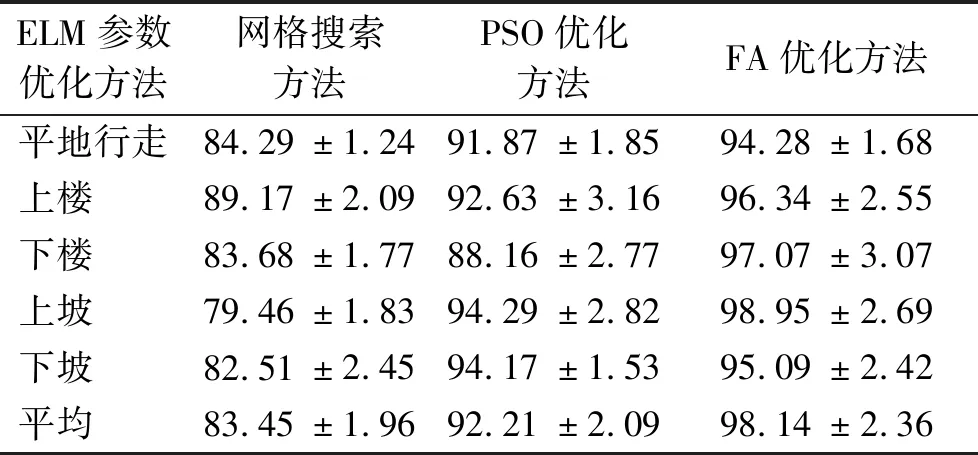
ELM参数优化方法网格搜索方法PSO优化方法FA优化方法平地行走84.29±1.2491.87±1.8594.28±1.68上楼 89.17±2.0992.63±3.1696.34±2.55下楼 83.68±1.7788.16±2.7797.07±3.07上坡 79.46±1.8394.29±2.8298.95±2.69下坡 82.51±2.4594.17±1.5395.09±2.42平均 83.45±1.9692.21±2.0998.14±2.36
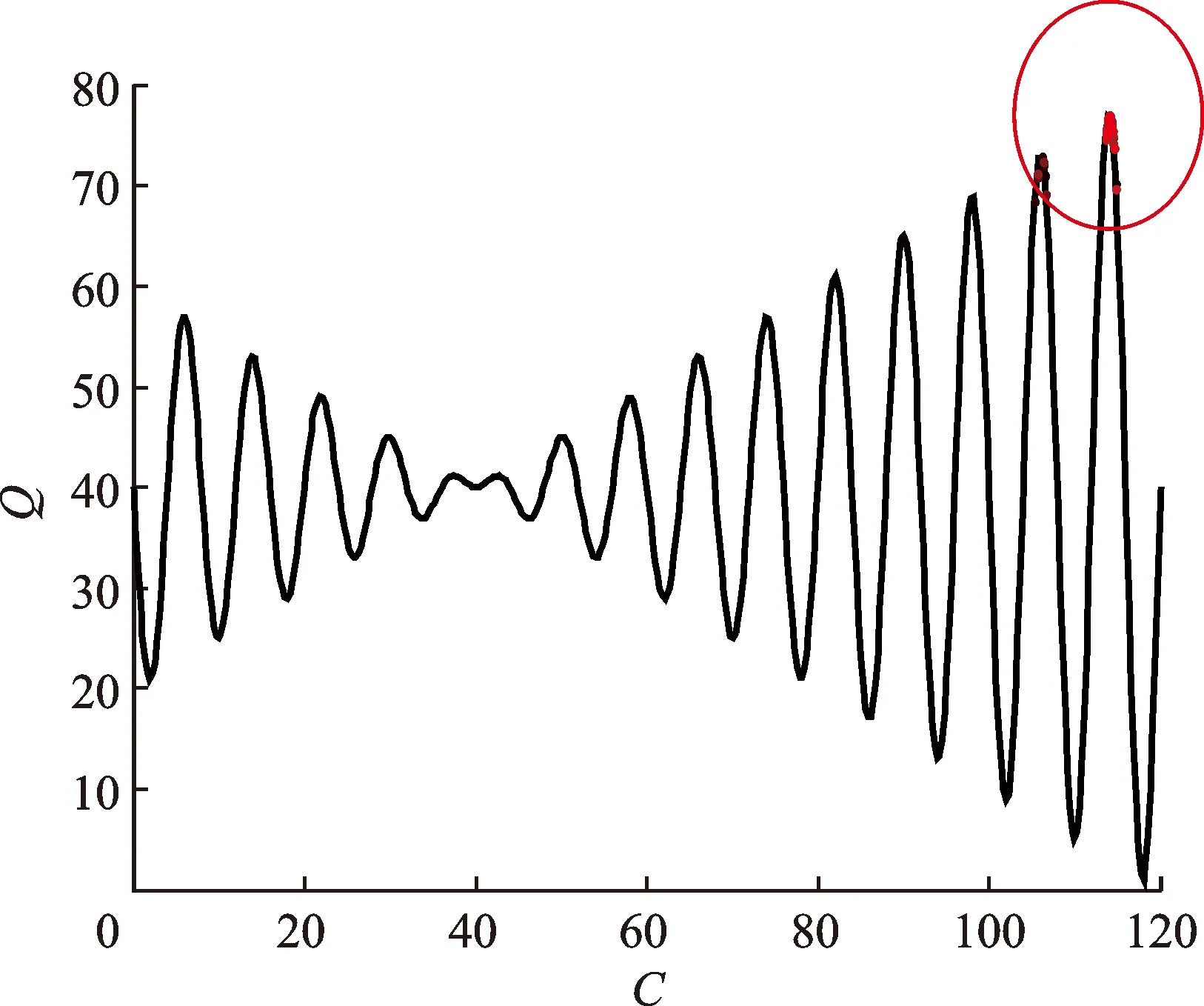
图7 最优解的变化
2.5 不同方法比较分析
为了说明本算法的有效性,做了对比实验,用笔者所述的特征提取方法提取的张量特征作为特征值输入BP神经网络、SVM和ELM分类器。对于训练集和测试集数据都使用 10 折交叉验证分类效果,如表3所示。鱼群算法进化ELM作为分类器的假肢步态识别方法,对每种步态的识别率均达到 90.45%以上。由表3可以看出,笔者提出的鱼群算法进化ELM算法明显优于传统的 BP 神经网络、SVM等方法,这主要是因为BP神经网络易于陷入过学习,导致识别率不高。ELM方法5种步态的识别准确率与BP算法比较有不同程度的提升,其中平地行走识别率提升较少,提升了2.15%,下楼提升最多,提高将近6.73%。AF-ELM分类器的识别率高于没有经过参数优化的ELM分类器,说明优化后的ELM得到全局最优解,使步态整体识别率得到改善。
本研究使用的计算机平台为32位 Windows操作系统,2.50 GHz Intel core Quad CPU 处理器,4G 内存,Matlab R2010b 软件被用于分析与处理实验数据。5种步态不同算法分类时间如表4所示:BP神经网络学习速度较慢;而SVM由于采用一对一多分类模型,每次只能区分 2 种步态,SVM 分类器在步态平均识别时间方面高出ELM近 17.85%;由于ELM不需要调整网络输入权值,其分类时间小于SVM;而本研究采用的FA-ELM的识别时间长于ELM方法,但是其识别平均准确率为97.45%。因此最终选择 FA-ELM分类器进行分类识别。

表3 不同分类器的步态识别准确率比较
表5给出了识别时间的比较,识别时间包括特征提取、特征值降维和分类识别的时间。张量投影方法能够从时间、空间等多个模态上提取肌电信号的有效信息,然而高维度计算提高了算法的复杂度,带来了运行时间较长的问题。张量投影通过PCA降维处理后,有效缩短了分类时间。张量投影特征结合PCA降维处理后能够综合反映步态特征的结构信息,缩短了分类时间。FA参数优化方法能够更准确、更有效地找到正则化参数和ELM 核参数的优化组合值,因此FA-ELM分类方法时间长于ELM方法。本研究方法可用于对识别精度有较高要求的离线分析中,在系统实时应用方面还有待改进。
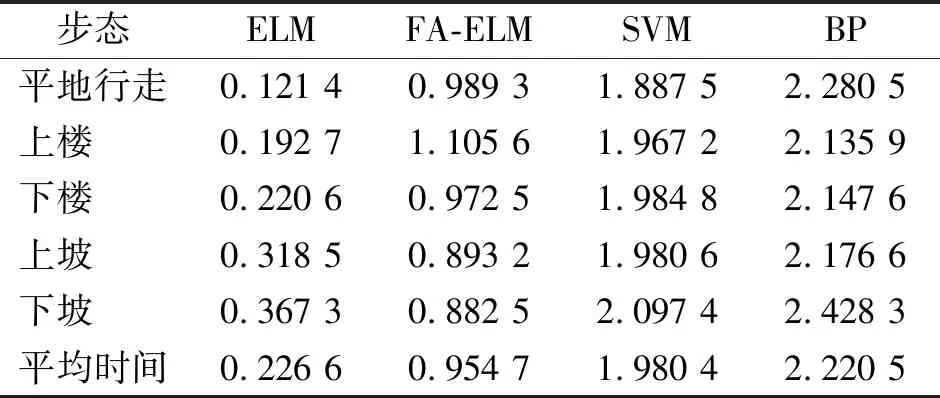
表4 不同算法分类时间比较

表5 不同算法识别时间比较
3 结束语
以表面肌电信号作为假肢步态识别信息源,提出了一种基于张量投影特征和FA-ELM的步态识别方法,可用于智能下肢假肢的步态识别。实验结果表明,鱼群算法进化ELM方法提高了下肢假肢的步态识别准确率,说明了将鱼群算法进化ELM方法用于下肢假肢步态识别领域的可行性与正确性。
