基于Duffing van-der-pol系统几何特征的材料非线性特征量化*

柏 林， 李兆昕， 刘小峰

(重庆大学机械传动国家重点实验室 重庆，400044)

引 言

在超声无损检测领域，由于Lamb波在缺陷形成的非均匀介质环境中传播时，其参数的变化能反映缺陷特征，因此常用于检测板结构的裂纹和疲劳损伤。传统Lamb波技术只能检测裂纹尺寸大于波长的缺陷，对早期的微小裂纹和疲劳损伤的敏感性不足[1]。非线性Lamb波技术对早期损伤十分敏感，缺陷引起的二次谐波信号中包含了大量的缺陷信息，二次谐波的幅值、相位等可以反映出缺陷的尺寸、材料非线性等特征[2-3]。但在实际运用中，早期损伤引起的二次谐波信号十分微弱，常被噪声所掩盖而造成漏检和失真，因此提高对二次谐波的检测能力和精度至关重要。

鉴于混沌振子系统具有对微弱信号敏感且对噪声免疫的特性，其在Lamb波检测技术中的应用已初见成效。张伟伟等[4]采用Duffing系统结合二分法识别仿真导波的发生时刻，但只局限于导波无法识别的缺陷。武静等[5]利用Duffing-Holmes混沌系统以及Lyapunov指数检测缺陷反射波实现了缺陷识别，虽然定义了损伤指数，但无法定量分析二次谐波幅值和缺陷尺寸。Jiao等[6]采用非线性Lamb波的模态分析对金属板结构缺陷实现定量分析，但无法对材料非线性的量化。刘海波等[7]提出了基于Duffing振子逆向相变的正弦信号检测方法，但该方法在量化调制信号时仍然存在局限性且抗噪性能有限。

1 Duffing van-der-pol系统动力学特性

Duffing van-der-pol方程不仅包括Duffing方程的三次非线性恢复力，还有van-der-pol振子方程维持自激振动的非线性项。Duffing van-der-pol系统表示如下

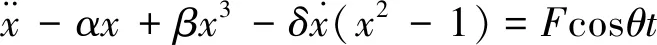
(1)

其中：α为线性系数；β为非线性系数；δ为阻尼系数；F为系统内部策动力振幅；θ为角频率；t为时间；x为自变量(无量纲)。

当θ=1以及α，β，δ确定且系统为临界混沌状态时，系统状态对周期信号十分敏感，即使信号很微弱也可以使系统由混沌转换为大尺度周期状态。为了使Duffing van-der-pol系统对任意频率具有普适性，需要对系统进行时间尺度线性变换。令t=ωτ，并输入待测信号s(τ)=Acos(ωτ) +n(τ)，其中n(τ)为随机噪声，将原系统方程换元求导后，转化为关于待测信号时间τ的系统方程，即

ω2(Fcosωτ+s(τ))

(2)

其中：τ为时间。

系统经过时间尺度变换后，在不改变系统参数和初始条件的情况下可以检测任意频率的谐波信号。

2 基于相轨迹的平均周期面积几何特征指数

由于Duffing van-der-pol系统不存在精确的解析解，因此策动力大小将影响数值解，使系统处于不同状态。在实验中发现，当系统处于大尺度周期状态时，策动力的微小变化也会直接反映在系统的输出响应中。如图1所示，在不同幅值的外加策动力激励下，系统解的幅值出现明显偏差。

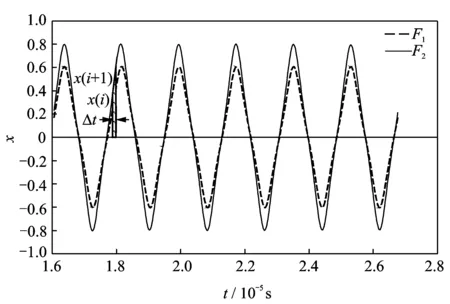
图1 平均周期面积示意图

文献[10]指出，策动力幅值变化与系统解的平均周期面积之间存在近似单调的线性关系，因此笔者将系统解的平均周期面积作为相轨迹的几何特征参数。利用4阶Runge-Kutta法求解系统方程后，计算图1中曲边梯形单元面积如下

(3)

其中：xi为输出在i时刻的值；Δt为系统解序列的时间间隔，即为梯形的高。

为使平均周期面积随系统解的变化更明显，对ΔS分类并取模

(4)

(5)

其中：k为周期个数。

3 基于平均周期面积的二次谐波幅值估计

(6)

(7)

(8)

(9)

二次谐波幅值定量分析具体步骤如下：

1) 根据Lamb波的激发频率及采样频率设置Duffing van-der-pol系统的检测频率ω和系统求解时步长Δt，并进行时间尺度线性变换；

2) 改变系统策动力并绘制系统分岔图，根据分岔图确定系统临界混沌状态的策动力F；

3) 截取实测Lamb波波包，由于信号时长极短且波包边缘存在扰动，对波包汉宁加窗后周期延拓；

4) 由于二次谐波相比基波信号幅值相差几个数量级，因此使用高通滤波器滤除基波信号；

6) 对延时后的信号乘以ε∈[2, 4, 6, … , 240]的比例系数，并使用Runge-Kutta法求解系统方程，相轨迹若进入大周期则二次谐波存在；

9) 由步骤7和步骤8得到的拟合关系，并根据式(9)计算得到A2，即可表示二次谐波的幅值。

4 实验分析

4.1 实验装置

如图2所示，激发装置产生的Lamb波在非线性金属材料中传播一定距离后被接收，Ritec SNAP系统RAM-5000生成中心频率为0.28 MHz的非线性Lamb激励信号。实验材料为1.5 mm×630 mm×2 500 mm的铝板，无约束平行放置在海绵块上。换能器发生的脉冲群被放大后进入楔形树脂玻璃块，纵波通过楔形块边缘折射后传递至铝板，形成S0模态Lamb波。S1和A1模态能激发二次谐波累积[11]，根据近几年研究成果，S0模态也可形成二次谐波累加效应[12]。传递700 mm后由PZT传感器接收，并由RAM-5000采集输出至计算机，通过分析输出信号的频率成分，得到基波和二次谐波的幅值，并量化分析材料的非线性特征。

图2 Lamb波实验测试平台

4.2 Duffing van-der-pol系统参数设置

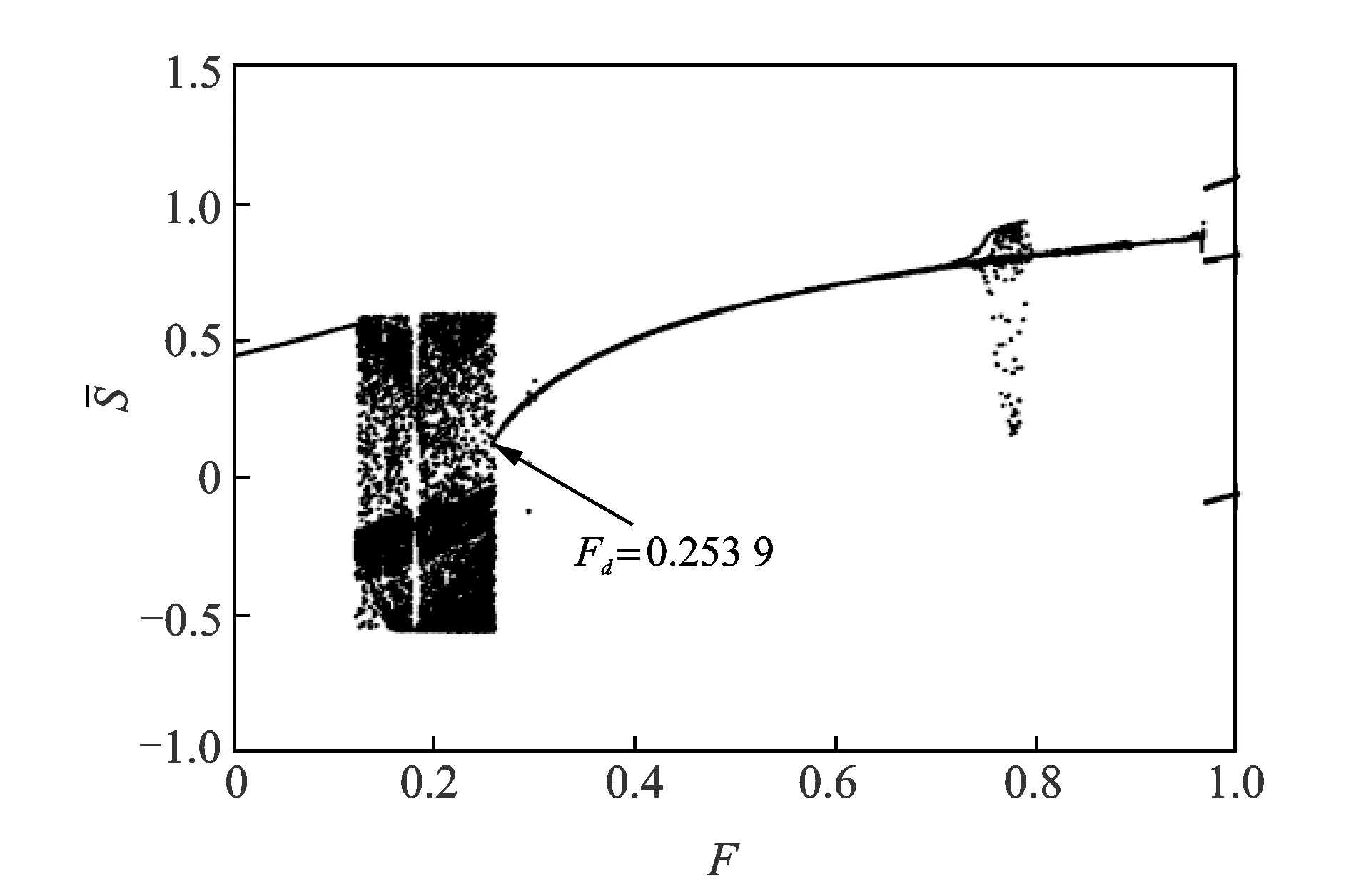
图3 Duffing van-der-pol系统分岔图

此时，输入微弱信号可引起系统由临界混沌转变为大周期状态，因此该系统对微弱信号具有较好的敏感性，可作为二次谐波定性分析时系统参数F。

4.3 实测信号处理及二次谐波定性分析

截取实测信号中Lamb波波包作为分析对象，二次谐波的幅值相比激励信号十分微弱，相差约80倍。所以在测量过程中，若存在微弱的噪声干扰，二次谐波就会失真，并影响到材料非线性特征分析的准确性。为了模拟受到噪声干扰的情况，在原信号中加入标准差为4×10-4V的白噪声，如图4所示。观察频谱可知，原始信号的二次谐波幅值A2=3.278×10-5V，加入噪声后为4.554×10-5V。二次谐波已经被噪声淹没，原本在0.56 MHz处的峰值发生漂移，幅值失真严重。

图5 不同系统状态的相轨迹

在100个周期的时长内求解系统，为了判断系统何时进入大周期状态，选取X(t)序列每个周期的极大值组成一个序列，如图6所示。从第40个周期以后，每个周期的极大值趋于稳定并保持大于0.78，因此将X=0.78设定为判别进入稳定大周期的阈值。为了避开混沌状态向大周期的转换点，在此基础上再向后延长3个周期，从第43个周期开始向后截取50个周期相轨迹计算平均周期面积。

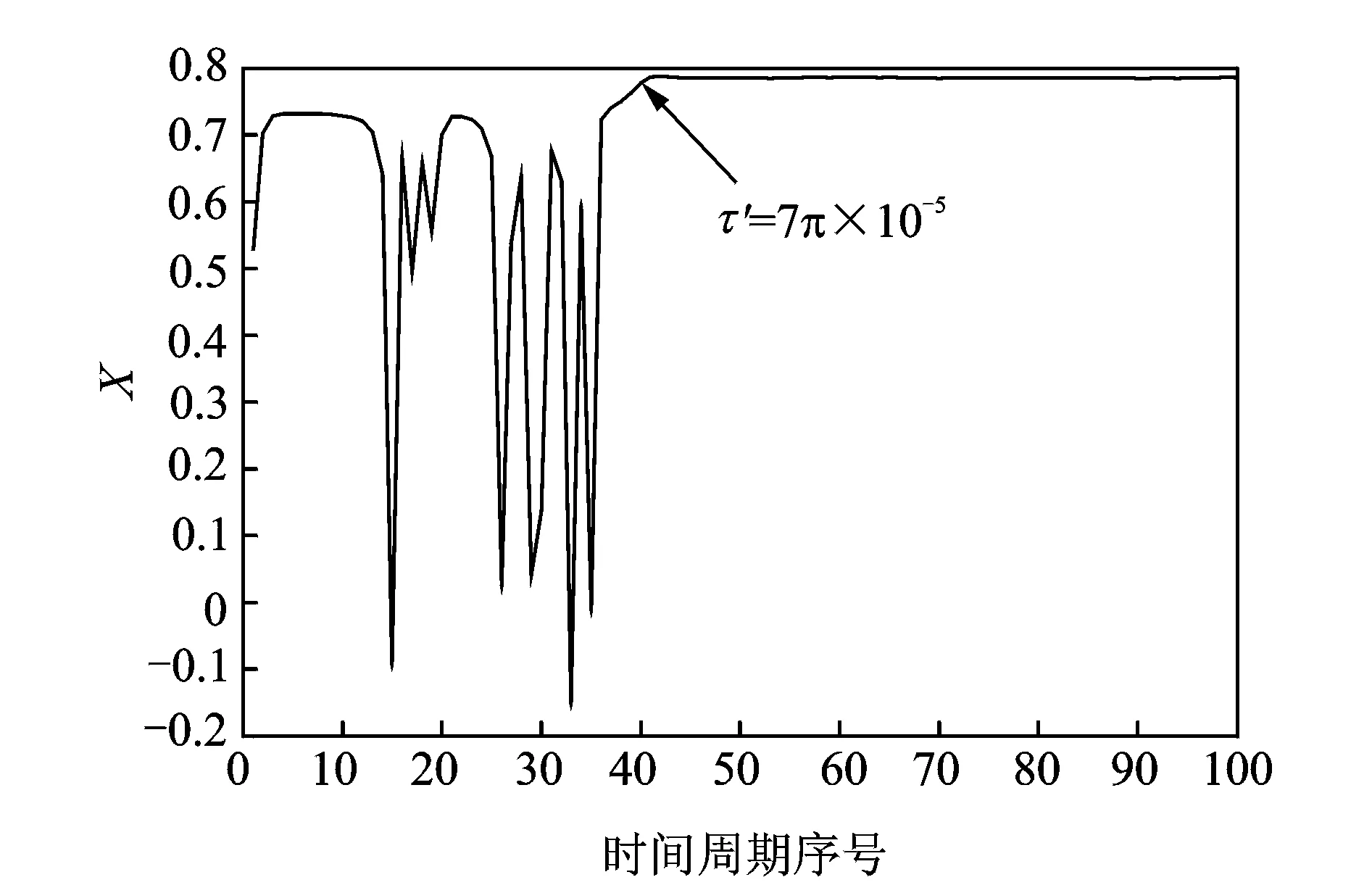
图6 X(t)在每个周期的极大值

4.4 基于平均周期面积非线性指数分析

图7 系统策动力F与拟合关系

(10)

图与延时τ拟合关系 图与比例系数ε的拟合关系

表1 不同算法计算二次谐波幅值对比

Tab.1 Comparisons of second harmonic calculated by different methods

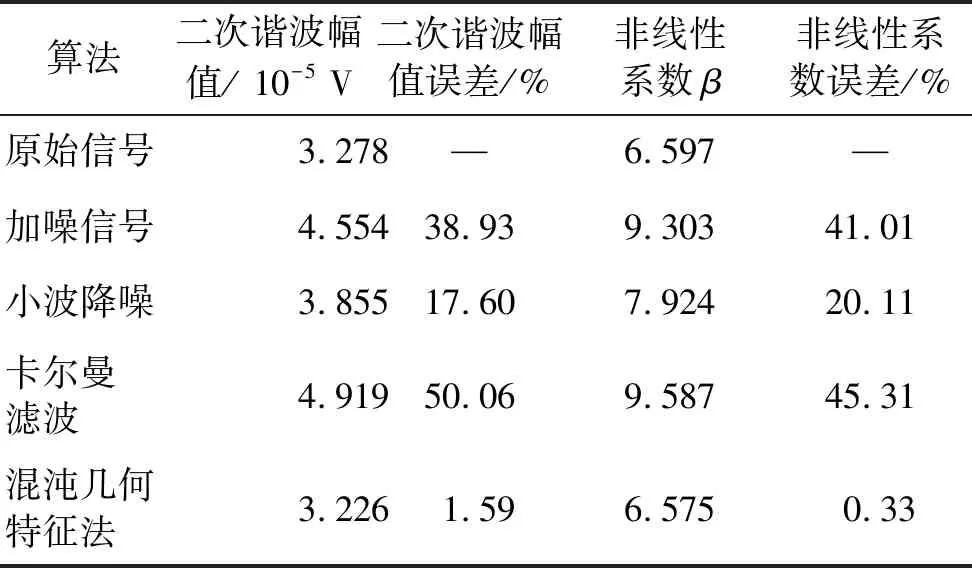
算法二次谐波幅值/ 10-5 V二次谐波幅值误差/%非线性系数β非线性系数误差/%原始信号3.278—6.597—加噪信号4.55438.939.30341.01小波降噪3.85517.607.92420.11卡尔曼滤波4.91950.069.58745.31混沌几何特征法3.2261.596.5750.33

5 结束语