言语与符号：培育数学思维的重要表征

冯桂群

“小学数学教学的核心问题是适度抽象，谋求儿童思维的形象性与数学抽象性的协调统一。”[1]而在实际教学中，数学教师往往比较重视借助动作表征和形象表征培养学生的动作思维和形象思维，但在如何借助言语和符号表征发展学生的抽象逻辑思维方面，还重视不够、研究不够，导致在实际学习中，儿童的思维总是难以及时地由感性层面提升到理性层面，或是快速地由抽象层面穿梭到形象或是具象的层面，进而影响学习效果的达成和数学核心素养的提升。

那么，如何借助言语表征和符号表征，有效提高学生解决实际问题的能力，进而培养学生的抽象思维，渗透抽象、推理、建模等数学思想呢？下面就结合相关教学实践，谈谈自己的一些做法与想法。

一、言语与符号表征让数学思维的“提升”事半功倍

我们在引导学生进行数学“建模”活动时，首先要通过实物操作或手势操作经历动作表征过程（已有相关活动经验积累的，此步可省略），之后通过想图、画图、看图等操作经历形象表征过程，其间要适时插入言语表述，以及之后的标注符号或列表，书写关系式、公式、算式等数学符号的表征活动，让学生经历符号表征过程，使实物、手势、图形、言语和符号等直观、半直观、半抽象、抽象的多元表征，有序地成为学生思维的脚手架，使学生的思维顺畅地由动作水平上升到表象水平直至抽象水平，使思维断层自然消失，使思维的提升“事半功倍”。

1.让数量关系的梳理唾手可得

数学是研究客观数量关系和空间形式的一门科学，具有高度概括性、逻辑严密性、应用广泛性等特点。要想让学生准确理解某个具体问题的数量关系，借助摆弄学具或画图呈现，学生可能一下子就明白了，但要由此迁移到解决一类问题，尤其是当实际问题中的数据很大，不可能通过摆一摆或画一画解决时，言语与符号表征就显得特别重要了。

如教学苏教版《数学》六年级上册的“假设策略”例2：在一个大盒和5个同样的小盒里装满球，正好是80个。每个大盒比每个小盒多装8个，大盒里装了多少个球？每个小盒呢？学生借助书上的示意图和小组合作，很快找到了以下几种方法：将1大盒看作1小盒，总量少8个，每小盒个数是（80—8）÷（5+1）=12（个）;将5小盒看作5大盒，球总数会多出5个8，每大盒个数用（80+5×8）÷（5+1）=20（个）;设每小盒有X个，每大盒有（X+8）个，方程是X+8+5X=80，同样能算出结果。此时，笔者没有让学生就题论题、浅尝辄止，而是引导学生深入反思：这3种解法都是紧紧抓住大盒和小盒间的什么关系来列方程或列算式的？于是在师生互动中，抓“总和句”列等式、抓“相差句”来假设的思路就形成了：

借助列关系式和标注符号，假设的思路清晰而深刻。之后引导学生看着“可视化”的符号导图，用简洁的言语表述假设的两种思路（略）。有了言语表征、符号表征的及时介入，学生在直观理解的基础上将数量分析符号化、可视化和流程化，使解题方法结构化，并最终甩掉对“直观图示和小数目”的依赖，实现对深藏的和差关系的精准把握和形式化表达。

2.让算理算法的理解易如反掌

在教学乘法或除法的初步认识时，教师会引导学生先进行摆小棒或做手势的动作表征，之后借助看图、想图和画图等图形表征来理解乘法或除法的具体含义，最后实现概念的内化和符号化的表达。而当学生的经验和知识积累到一定程度后，对算理和算法的理解与建构就完全摆脱了现实模型和图形表征，仅靠数学世界里的概念、判断和推理来实现。此时，让学生借助言语和符号表征来进行抽象思维和演绎推理，就显得尤为重要。

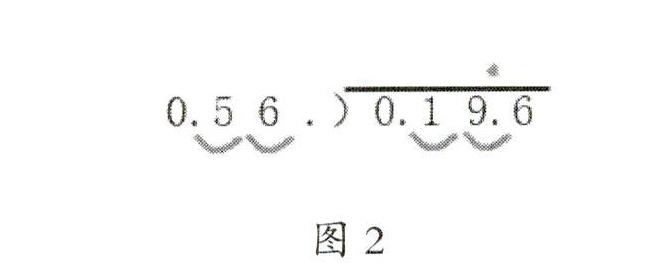
如笔者引导学生借助符号表征和言语表征，巧妙地“视听”小数除法的算法和算理。在计算0.196÷0.56时，引导学生通过画2组弧线和点3个小数点，清晰地表征小数点的处理过程，同时有条理地进行言语表述：除数是小数，先将除数的小数点向右移动2位，使它变为整数;要使商不变，被除数的小数点也要向右移动相同的位数;商的小数点和被除数移动后的小数点对齐。同时追问：为什么除数和被除数的小数点都要向右移动2位？为什么商的小数点只能跟被除数移动后的小数点对齐？最后，引导学生用言语概括出小数除法的一般算法。至此，学生不仅掌握了小数除法的算法和算理，还感悟了渗透其中的转化思想，提高了语言概括能力和有序思考能力，增强了用数学表征来思考数学的信心与技巧。

3.让数学模型的建构水到渠成

在由实际问题抽象成数学模型的建模过程中，借助实物或手势进行的动作表征，以及借助想图、看图、画图来进行的形象表征固然重要，但之后借助言语表述、符号标注、列表列式等进行的抽象表征更为重要。它甚至是建模成败的关键，是培养学生抽象思维的重要抓手。

如苏教版《数学》i年级下册的“长方形和正方形的面积计算”，由于教材中只安排学生被动地用l平方厘米的方格摆、量、算3个较小的长方形面积，学生的操作活动一直在低层次打转转，做得多想得少，学生的动作思维跟形象思维、抽象思维间出现了断层，教学效果欠佳。为此，我们引导学生按选方格、摆方格、算方格的步骤，分别去测量邮票、作业封面、教室地面的面积。测量中，引导学生由摆满方格到只摆部分方格，再到用一个方格去摆，直至在头脑中摆方格，思维难度逐步加大。而每次操作活动中，都引导学生边看实物或图形，边有序进行言语表述与符号填写——“选面积l平方（）的方格去测量，每行摆（）个方格，摆（）行，一共是（ ）×（）方格，面积是（ ）”，从而强化了“求长方形面积，就是看一共包含多少个面积单位”的知识内核，使面积计算模型的建构水到渠成。借助与实物或图形相对应的言语与符号的及时抽象，数学思维的断层瞬间弥合，学生的空间观念真正实现由“一维”到“二维”的飞跃，并为以后学习用立方格去测量三维空间的物体体积，埋下了思维生长的种子，培育了结构化认知、系统性思维。

二、言语与符号表征让数学思维的“穿越”靈动自如

在数学学习中，帮助学生及时实现由动作思维到形象思维再到抽象思维的提升，是数学建模能否顺利达成的关键;而在应用模型过程中，则要着重引导学生借助动作表征、形象表征，尤其是借助言语表征和符号表征，将实际问题由抽象变为形象、由繁杂变为简单，将解题思路由模糊变为清晰、由内隐变为外显、由艰涩变为流畅，让思维在具象、形象和抽象间顺逆穿梭、自由跳跃、灵活转换，进而让学生在实际运用中更好地提升数学理解力和执行力、培养实践能力和创新精神。

1.让解题思路的呈现一目了然

苏教版数学教材中安排了解题策略的教学，目的是引导学生借助画图、列举、列表等策略成为思考的高手。其实，在解答一些老大难问题时，我们还可以引导学生在理解的基础上，用共同约定的符号或言语来“固化”解题流程，让解题思路的呈现一目了然、耳熟能详。

比如，在解答“小强用5米长的铁丝做了8个完全一样的‘九连环。做一个‘九连环需要铁丝（）/（）米，1米长的铁丝可以做（）/（）个？”等有关分数除法的

实际问题时，学生一开始很容易出错。因为他们将这类问题跟“求A是B的几分之几”的问题混为一谈，常用问题中先出现的量，去除以后出现的量。为此，我们先以学生幼儿园时就会解答的问题“平均每人分得几块糖”为例，让他们明确：最终求的是每份几块糖，不是每份几个人，所以要将“糖的总块数”平均分，关系式是“总块数÷总人数”;同时让学生用画圈来关注问题中的计量单位，用交叉的箭头进行符号标注（如图3中的标注），提醒自己是用后面的总数量去除以前面的总份数;同时引导学生用言语表述：做一个‘九连环要铁丝多少米，关键的单位名称是“个”和“米”，要求每份是多少米，要用“总米数÷总个数”;1 米长的铁丝可以做多少 ，关键的单位名称是“个”和“米”，要求每份是多少个，要用“总个数÷总米数”。有了以上的符号标注与言语表述，学生顿时醒悟，再想出错也不可能了。

2.让分率含义的解读一清二楚

在小学数学中，分数常常被认为是最复杂的数。有研究者认为，分数是一些小学生在数学学习中出现困难的实际起点，并由此在小学生的数学学习中出现了两极分化[2]。为了帮助学生攻破这一学习堡垒，尤其是帮助学生精准解读表示关系的分数——分率的含义，除了做手势、画图形等方法外，笔者引导学生创造性地用符号标注和言语表述来理解分数的含义，使学生在“守本分、抓份数“中思路澄澈、心如明镜。

如在解答苏教版《数学》六年级上册的分数乘法问题：吴大伯家去年收白果520千克，收的核桃比白果多2/5。收的核桃比白果多多少千克？收核桃多少千

克？笔者引导学生借助符号清晰解读分率2/5的含义，

即：（ ） ;言语表述：2/5是把白果的千克数看作“单位1”的量，平均分成5份，核桃多这样的2份，共7份。之后让学生以白果的千克数为标准，写出多个乘法或加法的关系式。在独立思考与全员互动的基础上，学生找到了4个关系式：白果千克数×2：多的千克数，白果千克数×（1+2/5）：核桃的千克数，白果千克数+多的千克数=核桃千克数，白果千克数×（1+1+2/5）：它们一共的千克数。有了这

样的深刻解读，之后的问题解答就轻松多了。

3.让数学推理的展开顺畅自如

人们在登山时，总要借助石阶、扶手，甚至是套在身上的绳索。同样，解答复杂问题时，言语与符号表征尤如救命的绳索，会让学生的抽象思维和逻辑推理安全行进，进而成功地培育他们的抽象思维与理性精神。

解答苏教版《数学》六年级下册的鸡兔同笼问题，教材上的方法一般有画图调整法、列表调整法、列方程解答法和直接列式解答法。笔者教学时，引导学生在头脑中想图的同时，借助符號标注与言语表述，及时地进行合情推理与逆向推理，让学生在符号世界里成功地完成理性推演，获得难题的破解和理性思维的提升。图4是一位学生上台板演的解题过程（题目：鸡兔同笼，共有头35只，脚94只。求鸡、兔各几只？）。板演后，向全班交流了他的思路：将其中的兔全部假设为鸡，那1兔看成l鸡，脚数就会少2只，那么脚数一共会少24只;24里有12个2，所以兔的只数就是12只，鸡的只数是23只。以上过程中的标注和列式，直击知识内核和思维要害，几乎被所有学生内化与活用;同时还无痕地渗透了抽象、推理、建模等数学思想，培养了理性化、结构化的思维方式和认知图式。

总之，我们要创造性地借助言语表征和符号表征，使学生的动作思维、形象思维和抽象思维得以生动、和谐、全面地获得发展，让学生的思维在具象、形象和抽象间自如提升、自由穿梭，从而培养学生的多元思维和理性精神，使数学核心素养的培育落地生根。

参考文献

[1]曹培英.“抽象”能否成为小学数学学科的核心素养[J]小学数学教师，2015（ Z1）.

[2]郑毓信.分数的教学与数学思维[J].小学教学：数学版，2010 （05）.

[责任编辑：陈国庆]