度量测度空间中障碍问题解的Caccioppoli 型不等式*

王会菊

(西北工业大学 理学院,西安 710129)

变分不等式和自由边界研究中出现的障碍问题受到很多学者的关注,例如一些学者在欧氏空间,Hörmander向量场等空间结构下对障碍问题展开了深入的探讨[1-3]。

度量测度空间(X,d,μ)包括了欧氏空间以及Hörmander向量场[4-6],X为集合,d为度量,μ为满足二重性条件的Borel正则测度。由于度量测度空间中的分析有助于建立更一般的理论和方法,因此度量情形下的凸积分泛函及障碍问题得到了广泛研究[7-9]。

本文在度量情形下研究Orlicz-Sobolev空间N1,Φ(Ω)中的障碍问题,其容许集形如

ω1≤v≤ω2a.e.}

(1)

(2)

则称u为Κω1,ω2,β(Ω)-障碍问题的解,式(2)中gu和gv分别为u和v的最小Φ-弱上梯度。

本文拟应用 “填洞法”,证明Κω1,ω2,β(Ω)-障碍问题的解满足Caccioppoli型不等式

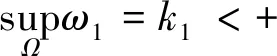
(3)

1 预备知识和引理

N-函数Φ(t)是定义在[0，+)上的严格单调增加的凸函数。若存在常数C1>1使得对任意的t≥0,

Φ(2t)≤C1Φ(t),

(4)

则称Φ(t)满足Δ2条件。

设u是定义在度量测度空间X上的实值可测函数,如果非负Borel函数g对任意的可求长曲线γ:[0,Iγ]→X，都有

(5)

则称g是u的上梯度。若存在非负可测函数g使得式(5)对一个Φ-模长为0的曲线族之外的可求长曲线都成立,则称g是u的Φ-弱上梯度．

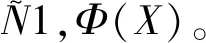
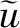
由文献[10] 可知,当Φ满足Δ2条件时,对于u∈N1,Φ(Ω),存在u的最小Φ-弱上梯度gu∈LΦ(Ω)，使得对u的任一Φ-弱上梯度g,g∈LΦ(Ω),在Ω上几乎处处成立

gu≤g

(6)

下面给出最小Φ-弱上梯度的三个性质,详见文献[8]。

性质1 若u1,u2∈N1,Φ(Ω),则在Ω上几乎处处成立

gu1+u2≤gu1+gu2

(7)

性质2 ① 若u∈N1,Φ(Ω),c是常数,则gu在集合{x:u(x)=c}上几乎处处为0。

② 若u1,u2∈N1,Φ(Ω),则gu1和gu2在集合{x:u1(x)=u2(x)}上几乎处处相等。

性质3 若u1,u2∈N1,Φ(Ω),则|u1|gu2+|u2|gu1是u1u2的Φ-弱上梯度。

2 定理1的证明

证明设B(z,R)⊂⊂Ω,0<ρk}，在ΩA(k,R)上有gv=gua.e.于是

(8)

(9)

结合式(8)和式(9)得到

(10)

(11)

因为Φ是严格单调增加的凸函数,所以由式(10)和式(11)可得

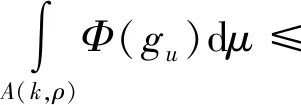
(12)

又因为在B(z,ρ)上η=1,所以由式(12)可得

(13)

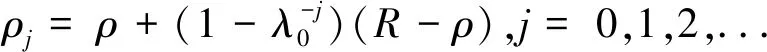
(14)

其中λ0满足

(15)

对任意的t≥0都成立。由文献[8]中的引理 2.1可知,这样的λ0是可以找到的。于是由式(13) (将ρ换为ρj，R换为ρj+1) 直接计算得到

(16)

可断定对任意的自然数N,

(17)

事实上,当N=1时,由式(16)可知式(17)成立。假设式(17)对N-1成立,即

(18)

令式(16)中的j=N-1并代入式(18)右端最后一项即得到

因此式(17)成立。

结合式(15)和式(17),以及cθ/(c+1)<1,可得

又因为在B(z,ρ)上g(u-k)+=guχA(k,ρ)几乎处处成立,可得

(19)

同理可证

(20)

结合式(19)和式(20)，即得式(3)，定理1得证。

3 结 论

本文在度量情形下利用 “填洞法” 得到了Orlicz-Sobolev空间中的障碍问题解的 Caccioppoli 型不等式。该定理推广了文献 [7] 中的引理 4.1和引理4.2，并表明在讨论Κω1,ω2,β(Ω)-障碍问题解的有界性时,由ω1的有界性考察解的上界,由ω2的有界性考察解的下界。结论丰富了度量测度空间中的非线性位势理论,并为进一步研究障碍问题解的有界性奠定了基础。