舰载火箭弹垂直发射系统流场数值仿真*

杨 戬,王敏毅,黄朝学,宋向华

(中国船舶重工集团公司第710研究所, 湖北宜昌 443003)

0 引言

多管火箭炮武器系统具有瞬时提供强大压制火力、发射多种性能火箭弹、快速再装填等优点,广泛应用于陆军、海军和空军等作战单位中。为适应现代高科技战争环境,对火箭炮武器系统提出了更高的性能要求,如低发射特征、隐身、精确打击等[1-3]。

目前火箭炮发射方式主要采用火箭发动机敞口发射,该种发射方式存在如下缺点：在车辆、船舶、飞机等对空间要求较高的作战平台上,火箭炮占用面积大、在高低和方位上存在不同程度的发射死角；同时火箭炮发射时,火箭弹的尾焰向外喷射,产生了较强的声光信号,不利于火箭炮的隐蔽。

为此,发展新的火箭弹发射技术显得尤为重要,文中基于导弹垂直发射技术,对舰载火箭弹采用垂直发射方式的可行性进行了初步探讨,分析了火箭弹发射过程中装置内部的燃气流场特性,给出了装置内部压力曲线,为垂直发射系统的设计和改进提供了理论依据。

1 计算方法

为了真实模拟出火箭弹发射过程中的燃气流场,需要建立合适的描述燃气流场特性的数学模型。由于火箭弹点火时喷出的燃气流速度很高,故将燃气看作可压缩气体处理,且不考虑燃气中固体颗粒的影响[4-6]。三维、雷诺平均的Navier-Stokes方程组如下：

质量守恒方程为：

(1)

动量守恒方程为：

(2)

能量守恒方程为：

(3)

式中ρ,u,p,E分别为燃气流密度、速度矢量、压力和总能。

以有限元体积法为基础,紊流模型采用k-ε二方程模型：

Gk+Gb-ρε-YM

(4)

(5)

紊流粘性系数为：

(6)

数值模拟采用FLUENT软件中的耦合显示算法。具体求解步骤为：先联立求解质量、动量和能量守恒方程,再利用所得的值求解紊流模型方程,最后用流体元的k和ε计算紊流粘性系数ui。

2 模型建立及网格划分

2.1 几何模型

数值计算时采用的垂直发射装置物理模型如图1所示,装置由压力室、排气道和火箭发射箱组成。压力室分为多个发射位,每个发射位上可安装一个火箭发射箱。

图1 发射装置模型截面图

本次仿真中只考虑单发火箭弹的发射过程,故模型可简化为如图2所示。

图2 发射装置发射单元模型

2.2 计算模型

弹体与发射管之间的间隙小于1 mm,忽略燃气通过缝隙的回流,最终简化的计算模型如图3所示。

图3 装置简化模型

2.3 网格划分

通过网格无关性分析,最终确定网格数量为350万个。网格的划分如图4、图5所示,在发动机喷管处进行了网格加密处理。

图4 计算模型全局网格划分示意图

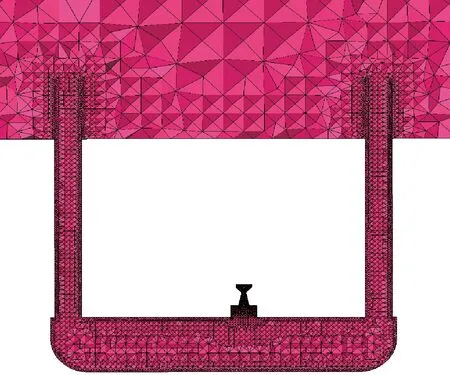
图5 发动机喷管处网格示意图

3 参数设置

3.1 计算参数

在计算过程中作出如下假设：忽略粒子流的影响以及粒子流与燃气的动量和能量交换；燃气热传导率和比热比恒定；燃气流的分子粘性系数符合Sutherland定律。

3.2 数值模拟初始条件设定

1)喷管入口边界条件以现有某火箭发动机参数给定为压强入口,分别给定燃烧室总温2 150 K、总压9.6 MPa；

2)外部流场出口为压强出口,理论上取大气无穷远处的环境状态作为燃气的出口状态,即压强为0.1 MPa,温度为300 K；

3)其余为绝热无滑移壁面边界条件,由于发动机工作时间短,不考虑管壁的散热问题。

数值模拟的边界条件如图6所示。

4 计算结果和分析

4.1 数值模拟结果

图7为装置底部压强随时间的变化曲线,装置底部燃气流正冲点压强较大,最大达到0.9 MPa。在实际设计中常采取底部加固或在底部增设导流格栅等措施来减小燃气流对装置底部的冲击。

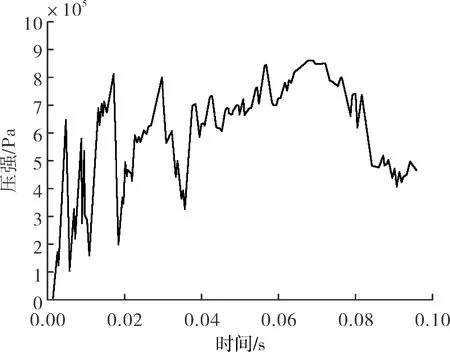
图7 底部压强变化曲线

图8为t=0.04 s时的底部压力云图,发射装置底部燃气流正冲点压强远大于其他区域,且正冲点附近压强梯度较大,从正冲点呈圆形等压线向外迅速下降到较低的压强。

图9为速度在火箭发动机内的分布情况,速度在喷管内发生了急剧变化,燃气尾焰沿着排气管排入大气。结合发动机内流场矢量图(图10),可以看出发动机尾焰排导较为顺畅,对弹体产生的增程力也较小,约为220 N,影响可忽略。

图8 装置底部压力云图

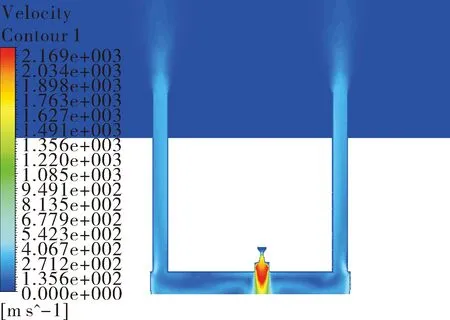
图9 发动机内速度分布云图

图10 尾流场速度矢量图

4.2 试验结果

结合某型火箭弹垂直发射试验,在发射装置底部的燃气正冲点以及排气管内关键点布置压力测试点,采用压力传感器进行在线测量,燃气正冲点附近的压力传感器测试结果经过300 Hz的滤波处理后的曲线如图11所示。

图11 试验压力曲线

从图11可以看出,火箭弹在发射过程中,装置底部的压强经历了从小到大再减小的过程,随着弹的不断升高,燃气正冲点的压强达到最大值。该试验结果和数值仿真的结果基本吻合。

5 结论

通过数值仿真,较为真实的模拟出火箭弹垂直发射过程中的燃气流场特性。由于燃气流本身成分复杂,且包含各种化学反应和两相流效应等[7],所以理论计算和实际情况存在一定的差别。但是数值模拟使垂直发射系统试验的风险得到了释放,也为发射装置的改进提供了理论依据。