基于QGA优化Simple-MKL的模拟电路故障诊断方法

莫凡珣， 马 峻， 陈寿宏， 徐翠锋

(桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004)

由于现代科学技术的不断进步，系统的规模越来越大，结构也日趋复杂，随之而来的问题是，系统一旦发生故障，不能准确分类和定位。近些年人工智能的方法被人们普遍采用，其强大的学习能力以及灵活性和普遍性在模拟电路故障诊断中得到充分发挥[1-2]。

核函数是支持向量机中非常关键的因素，因不同样本特征都有其符合的最佳核函数，文献[3-4]提出了多核学习算法。由于核函数的简单线性组合具有发挥不同核优势的特点，文献[5-6]提出了简单多核学习支持向量机模型[5-6]。近年来，支持向量机算法依靠其优越的分类能力而被广泛接纳，并尝试应用于模拟电路故障诊断的研究，但由于其在不同电路诊断中泛化能力弱等问题的凸显，加权改进混合核函数[7]、广义多核核函数[8]、信息熵[9]和粒子群优化算法[10]被相继引入，使得分类效果和泛化能力有了极大的提高。但在混合核函数中权重不易确定以及GMKL中正则化参数和折衷参数难于正确把握，而这些参数的选择对分类器的性能会有显著影响。

为解决上述问题，提出了一种由量子遗传算法(quantum genetic algorithm，简称QGA)优化简单多核学习(Simple-MKL)支持向量机模型的模拟电路故障诊断方法。首先，通过小波变换多分辨分析，归一化样本数据提取故障特征，然后利用量子遗传算法收敛速度快、易跳出局部极值的特点对多核学习支持向量机的惩罚因子以及样本比例进行优化，提高模拟电路故障诊断率。

1 Simple-MKL支持向量机

组合类型不同的核函数，可获得多类核函数的优势，就会得到更优的映射性能[11]。简单多核学习(Simple-MKL)支持向量机将不同种类核函数线性组合，形成新的核函数。多核核函数线性组合结构如图1所示。

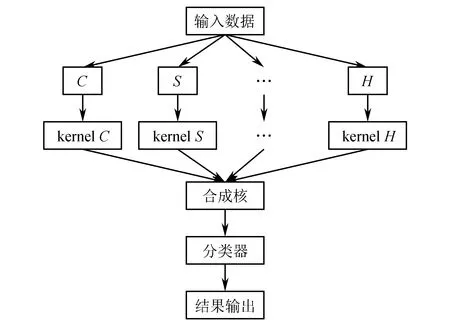
图1 多核核函数线性组合结构

(1)

其中：ai和bi为系数；K(x,xi)为再生核希尔伯特空间相关正定核函数[5]。选取的核函数为：

(2)

(3)

简单基本求核、加权求和核以及加权多项式扩展求和核为3种基本的线性多核核函数结合形式[6]。基本求核简单、高效，易于使用，其表现形式为

(4)

其中：M为核的总数；K(x,x′)为组合后的核函数；Km为每种单一核，Km可只选用一种核函数，也可选用多种不同的核函数[6]。

2 故障特征的提取和优化算法

在本诊断模型的优化方案中，首先对输入数据进行多分辨分析，利用归一化处理数据构造特征向量，其次，Simple-MKL支持向量机中的正则化参数和比例参数用量子遗传算法进行优化，从而对故障进行有效诊断。

2.1 小波变换与故障特征提取

小波变换是一种时—频联合域分析方法，可将待测时间信号由时域变换到时间—频率域，因此可观察出信号的时域和频域特性，从而得到信号的本质特征[12]。

连续小波变换的表达式为

(5)

其中：c为尺度因子，c>0；f(t)为待测量信号；τ为位移因子；φ(t)为小波基函数。一般将参数设为c=2j，τ=k2j，其中j、k都为正整数[14]，这样便于将信号中的高频因子和低频因子分离。小波分解示意图如图2所示。图2中，S表示最初信号值，A表示分离出的低频信号值，D表示高频信号值。多分辨分析对原始信号分离需达6层，将得到的1个低频系数序列和6个高频系数序列求平方和，形成故障特征向量集。由于数据量较大，为便于以下模型的快速建立，则需要用归一化函数将故障特征向量归一化至[0.1,0.9]，缩短了分类模型时间的建立。

图2 小波分解示意图

2.2 量子遗传算法

选用量子遗传算法对多核支持向量机中的重要影响因子寻优，演化操作的执行机构是量子旋转门[15]。量子旋转门的调整操作定义为

(6)

其中θi为旋转角。更新过程为

(7)

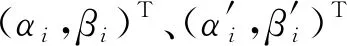
(8)

利用解空间变换将单位空间In=[-1,1]n映射到连续优化问题的解空间。在Simple-MKL优化模型中选目标函数

maxf(xi)=f(x1,x2,…,xn),i=1,2,…n

(9)

作为适应度函数，在解空间中，通过式(10)确定是否需要进化染色体得到最优值。

(10)

其中：pi为最优染色体的目标函数最优值，若值为p0，染色体需要更新，若值为pi，染色体不需要继续更新；i=1,2,…,N，N为种群的规模；f(xi)为适应度函数，表示故障诊断正确率；xi为第i个染色体值。

3 模拟电路故障诊断结构流程

故障诊断模型结构如图3所示。结合多分辨分析、量子遗传算法优化简单多核学习支持向量机模拟电路故障诊断流程如图4所示。

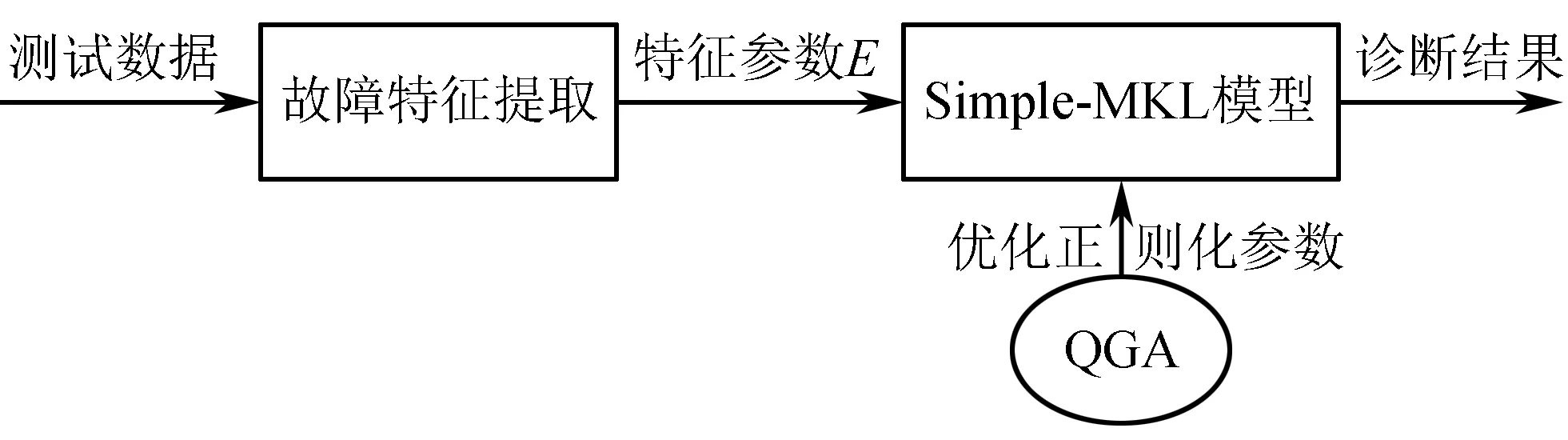
图3 故障诊断流程

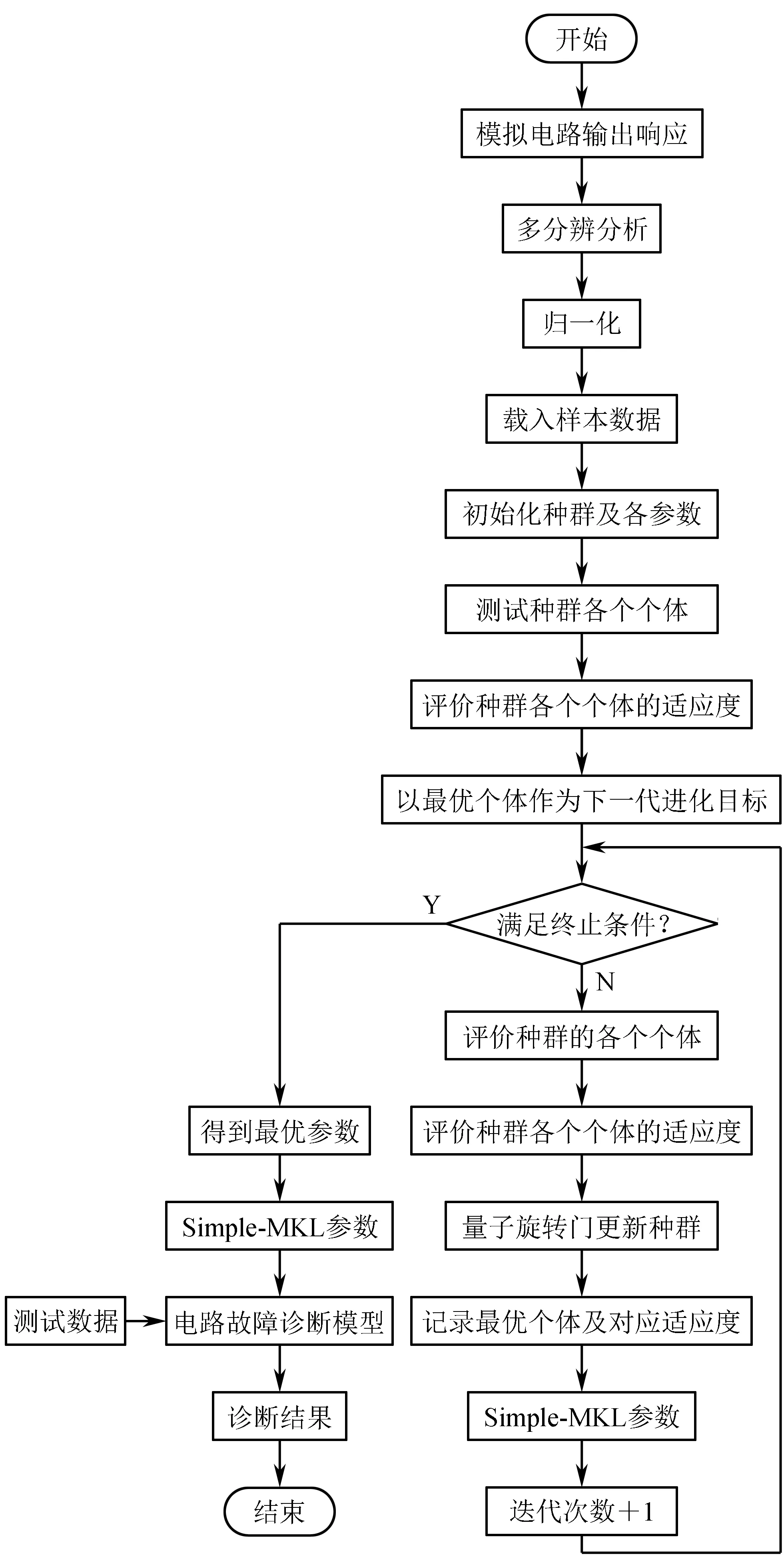
图4 故障诊断流程图

方法步骤为：

1)对模拟电路的输出响应提取参数，然后以多分辨分析(MRA)和归一化方式进行处理；

2)种群需初始化，产生随机量子比特αi、βi作为编码的染色体；

3)对初始种群中的每个个体依次测量，得出确定解xi；

4)对每一个确定解xi进行适应度评估；

5)保留最佳个体xi和对应的适应度函数f(xi)；

6)判断计算过程有无满足目标函数f(x)条件；

7)未达到条件则循环步骤2)和步骤3)；

8)利用式(7)量子旋转门整理得到新的种群；

9)重复步骤4)；

10)迭代次数加1，返回步骤5)；

11)若达到目标函数条件，则将最优参数作为Simple-MKL多核函数的参数建立模型；

12)将测试数据读入故障诊断模型，得到诊断结果。

4 实验与分析

故障诊断方法过程为：对原始时域信号进行6层多分辨分析，以Haar小波作为小波基，生成7维小波系数作为特征参量，归一化后即样本数据。为了识别不同的故障，基于样本数据应用QGA算法对Simple-MKL的参数进行优化，建立基于Simple-MKL的分类模型。

4.1 四运放高通滤波电路验证

图5为四运放高通滤波电路，假设电阻、电容发生软故障值在±50%情况下，图中所示out点是被测节点。利用Cadence电路仿真软件先对该电路做灵敏度判别，得出R1、C2、R3是对电路输出影响较大的电子元件，因此，选择R1、C2、R3为被诊断器件，所以，故障的模式设置为R1(1±50%)，C2(1±50%)，R3(1±50%)以及NF(正常状态)，故障模式共为7种。各元件的故障类型、标称值及故障值如表1所示。

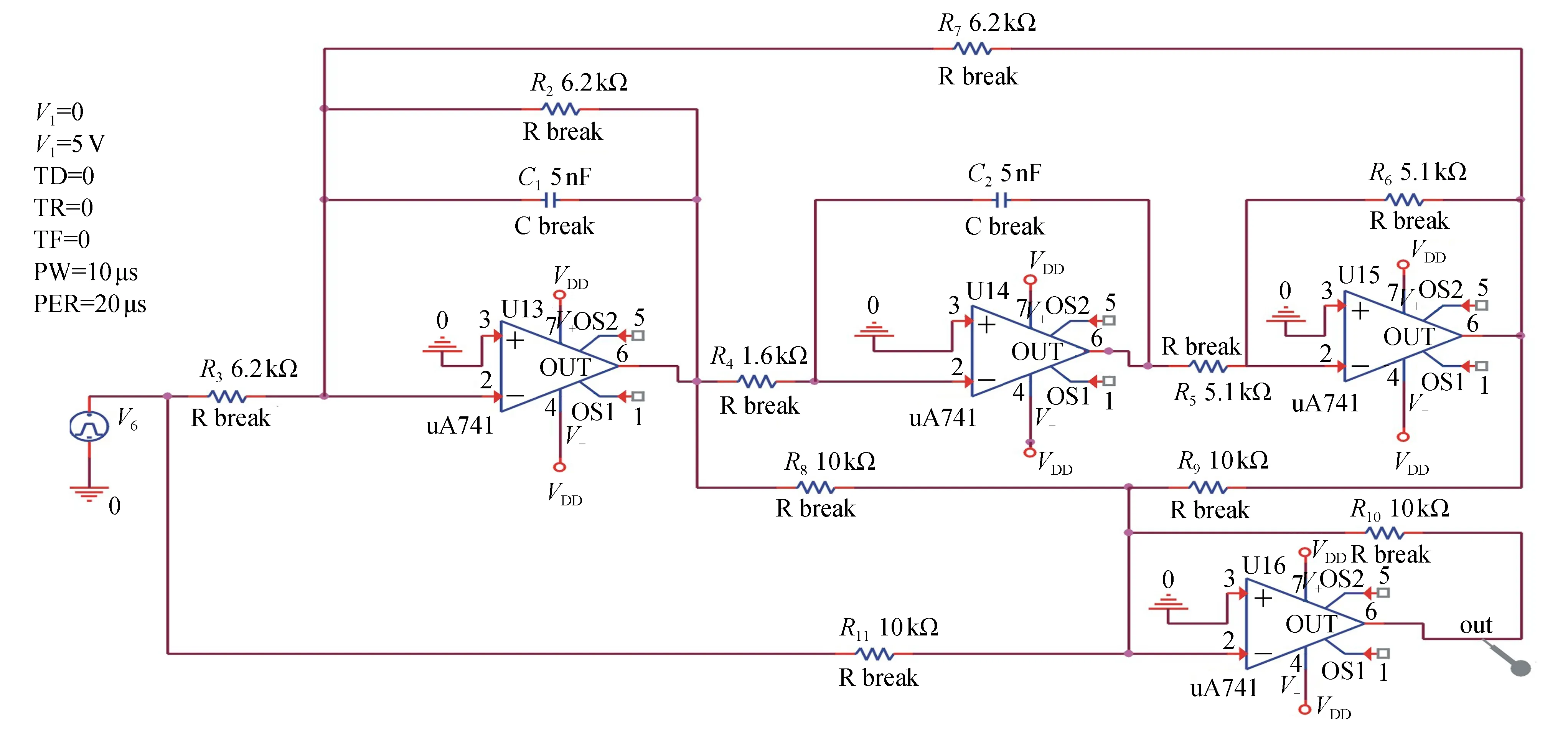
图5 四运放高通滤波电路

表1 四运放高通滤波器故障模式表

为了分离出训练数据集和测试数据集，采取了达100次的蒙特卡罗分析，分别对应电路中每一种故障状态，因此7种故障状态共生成700组故障数据。对于每种故障数据进行小波变换，分离变换出低频信号和高频信号的小波系数，每种小波系数同样随机选取500个点构造特征能量谱[16]。计算公式为

(11)

其中：Ej为频带为j的能量值，j代表1个低频和6个高频状态；sij为低频信号和高频信号的小波系数(i=1,2,…,K,K=100,j=1,2,…,7)。50组故障样本作为训练样本，剩下50组样本测试验证模型分类的诊断准确率。

初始化种群，转角大小和变异处理步骤进行启发优化。QGA中种群大小为10，进化代数为20。

Simple-MKL的核函数构建方式如下：

1)以数组[0.5,1,2,5,7,10,12,15,17,20]每个元素做宽度因子构建高斯核函数。

2)多项式函数的构建，分别以1、2、3为多项式核函数的次幂数。

可见，每个诊断实验中的Simple-MKL构建了91(13×7)个核函数。

以诊断正确率为适应度函数，其中惩罚因子和训练测试样本比分别为414.597 2和0.5。四运放高通滤波电路故障诊断率如图6所示。与混合核函数PSO-SVM[7]进行对比，本方法相较于文献[7]的方法，诊断正确率由99.5%提升至100%。

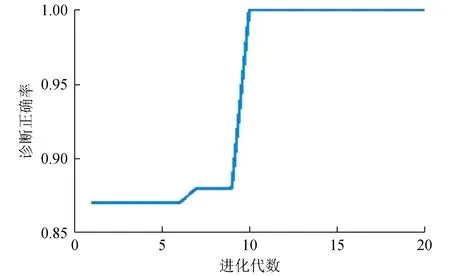
图6 四运放高通滤波电路故障诊断率

4.2 Sallen-key带通滤波电路验证

图7为Sallen-key带通滤波电路，作为验证模拟电路故障诊断率的最经典的电路。同样设置电路中电容容差为10%、5%作为电阻容差。假设电阻、电容都在50%的情况发生故障，图中out点为被测节点。电路灵敏度分析可知，C1、C2、R2、R3为故障元件。故障类型如表2所示。

图7 Sallen-key带通滤波电路

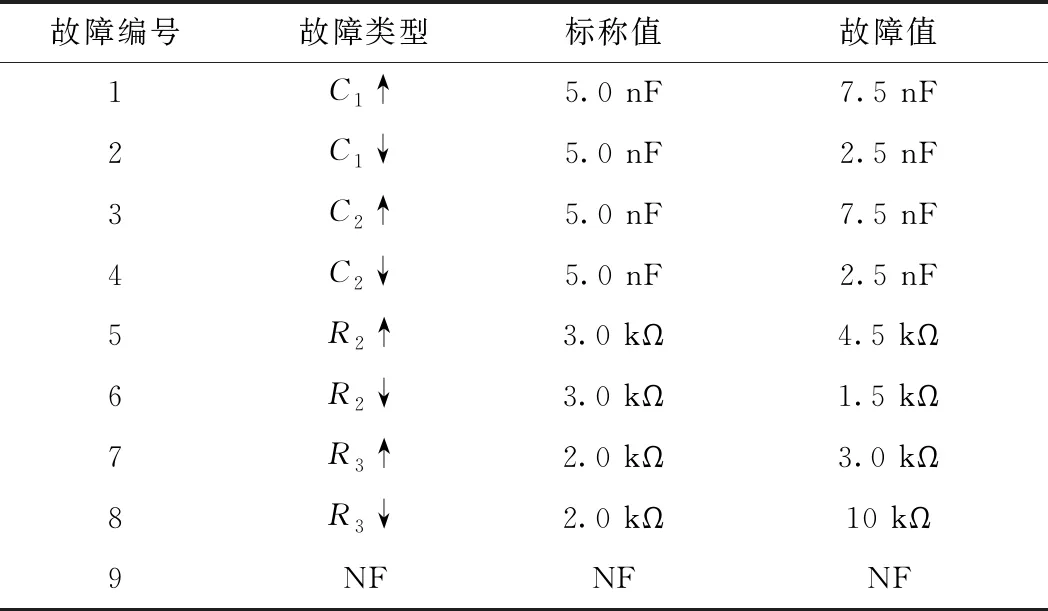
故障编号故障类型标称值故障值1C1↑5.0 nF7.5 nF2C1↓5.0 nF2.5 nF3C2↑5.0 nF7.5 nF4C2↓5.0 nF2.5 nF5R2↑3.0 kΩ4.5 kΩ6R2↓3.0 kΩ1.5 kΩ7R3↑2.0 kΩ3.0 kΩ8R3↓2.0 kΩ10 kΩ9NFNFNF

在Pspice电路仿真软件中，信号源输入为5 V的脉冲电压，脉冲宽度为10 μs，脉冲周期20 μs，供电电压15 V。对所有故障依次进行100次同等的蒙特卡洛分析，在图中out点处采取电压信号。然后进行小波分解再构造特征能量谱。训练样本和测试样本的比为1∶1。

Sallen-key电路故障诊断率如图8所示，QGA中种群大小为10，进化代数为20。构造91个核函数，其正则化参数为278.226 8，并与IPSO-SVM[10]进行对比，本方法相较于文献[10]的方法，诊断正确率由97.407%提升至100%。

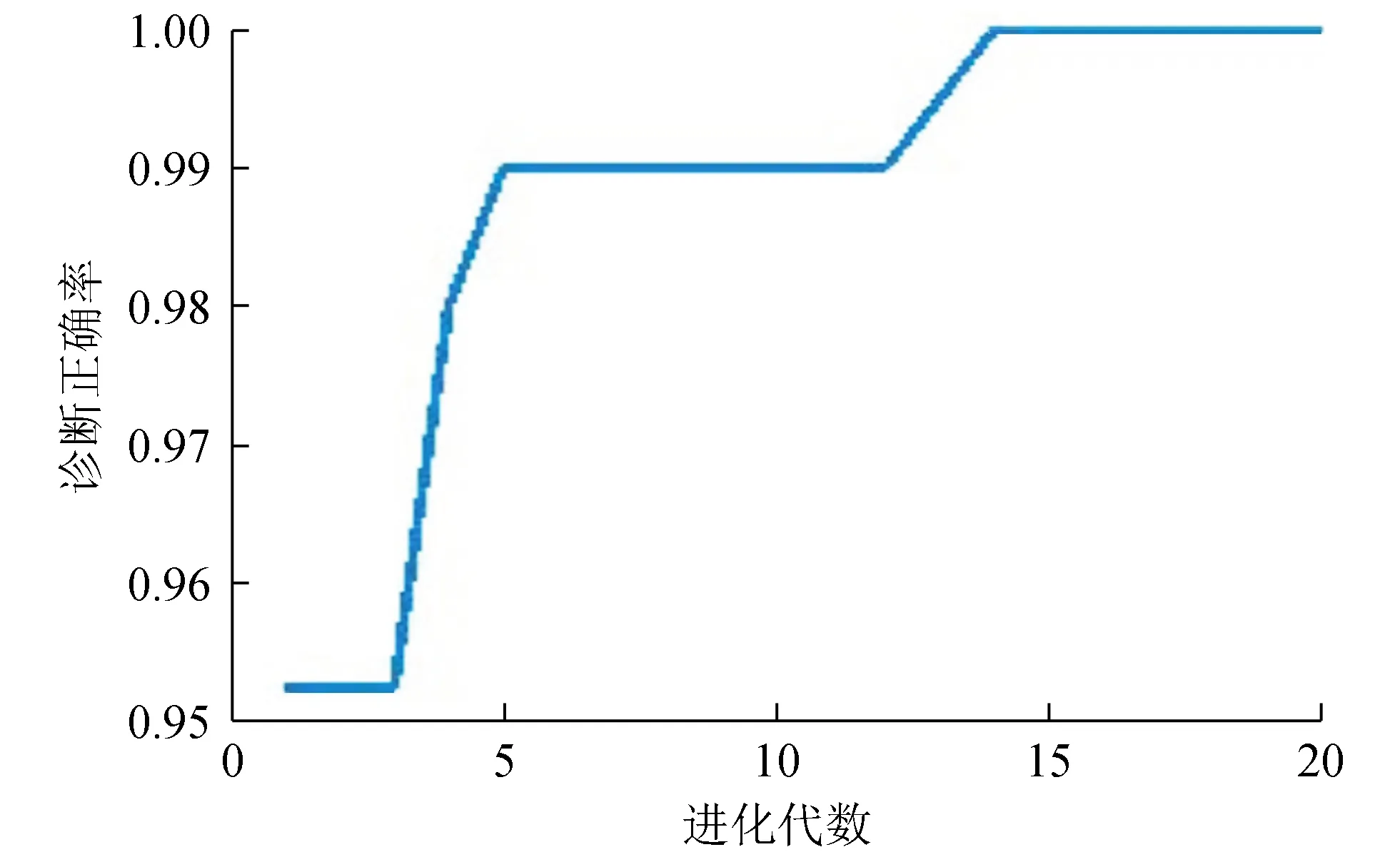
图8 Sallen-key电路故障诊断率

5 结束语

针对模拟电路故障诊断中传统支持向量机分类精度不高的问题，通过引入简单多核支持向量机，利用量子遗传算法对其进行优化,从而得到模拟电路故障诊断的方法。首先，对电路进行瞬态分析，采用多分辨分析提取电路故障特征；其次，用量子遗传算法优化简单多核支持向量机的参数，模拟电路故障的诊断，训练模型由此形成。仿真结果表示，本方法可以实现模拟电路故障诊断。另外，利用Simple-MKL建立模型的故障诊断时间也需要在进一步的研究中深入考虑。