基于变分模态分解和多尺度排列熵的滚动轴承故障诊断

张建财，高军伟

（青岛大学 自动化学院，山东 青岛266071）

滚动轴承是旋转机械的重要零部件，相关数据显示，由轴承故障导致的旋转机械故障大约占旋转机械故障的30%[1]。应用比较广泛的提取滚动轴承故障特征的方法首先是通过传感器采集轴承的振动信号，进一步对振动信号进行处理。常见的信号处理方法有局域值分解（Local Value Decomposition，LMD）、经验模态分解（Empirical Mode Decomposition，EMD）以及变分模态分解（Variational Mode Decomposition，VMD）。运用LMD 方法存在模态混叠、端点趋势无法预知等问题。EMD方法进行分解时对极值点搜索和载波包络线插值依赖性比较高[2]。VMD方法是新的典型的自适应信号处理方法，其通过非递归方法处理变分分解信号[3]。VMD方法能够突出信号的局部特征，在采样过程中和在抗噪声方面能表现出更好的鲁棒性[4]。本文主要采用VMD方法对提取的轴承振动信号进行预处理。为了量化基于VMD 方法得到的每个模态分量所包含故障特征信息，引入熵理论。排列熵(Permutation Entropy，PE)是计算时间序列复杂性的算法，对信号突变存在很强的敏感性[5]。但是，排列熵只反映时间序列在单一尺度上的信息，为了得到时间序列在多尺度下的复杂性变化信息以便更加全面提取故障特征，提出了多尺度排列熵(Multi-scale Permutation Entropy，MPE)，它可以表现出时间序列在不同尺度下的复杂性和相似性程度[6]。

本文将通过VMD 方法得到的模态分量采用多尺度排列熵分析，从而可更加全面提炼出轴承的故障特征信息。将得到的故障特征向量输入到PSOPNN 故障诊断模型中实现了故障类型的分类诊断，与未经过多尺度排列熵分析的结果相比提高了故障诊断的准确率。

1 VMD-MPE故障特征提取算法

1.1 变分模态分解

变分模态分解中假设信号由许多个模态函数叠加而成，每个模态函数可以看做存在不同中心频率的调幅调频信号[7]

式（1）中Ak(t)是非递减的，φ′k(t)≥0；Ak(t)≥0 且Ak(t)与瞬时频率ωk(t)=φk(t)相对于相位φk(t)来说是缓变的。在[t-δ,t-δ](δ=2π/φk(t))的时间间隔内，uk(t)可以描述成为一个幅值为Ak(t)、频率为ωk(t)的谐波信号。

通过迭代搜索构造的变分模型极值确定每个模态函数的频率中心和带宽，实现了信号的频域剖分及各个分量的有效分离，构造受约束的变分模型为

式（2）中：{uk}={u1,u2,…,uk}，为模态函数；{ωk}={ω1,ω2,…,ωk}，为中心频率为所有模态函数的和。

在式（3）中进一步通过引入惩罚参数α和惩罚因子λ，建立Lagrange 函数求出受约束的变分模型的最优解。

通过傅里叶变换将式（3）从时域转换到频域，并求解相应的极值，得到相应的模态分量uk、ωk

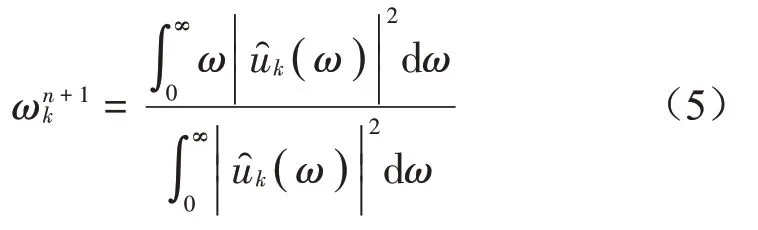
1.2 多尺度排列熵

多尺度排列熵首先是建立多尺度粗粒化时间序列，然后计算不同尺度下粗粒化序列的排列熵[8]，即多尺度排列熵。MPE 方法的引入使得时间序列的复杂性可以在多尺度下测量，能更加全面提取故障特征。具体计算过程为：

(1)设长度为N的初始时间序列为X={xi,i=1,2…N},对其进行粗粒化得到一个新的序列为

式（6）中S为尺度因子；[N/S]表示取整。

(2)对y(s)j进行时间序列重构可得

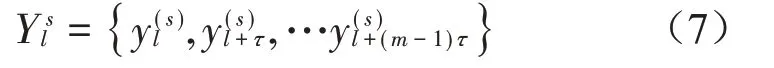
式（7）中l表示第l个重构时间分量；τ表示延迟时间；m表示嵌入维数。

(3)将式（7）得到的重构时间序列按升序排列可得S(r)= (j1,j2…jm)，r=1,2,…R(R≤m!)，得到符号序列出现的概率Pr(r=1,2,…,R)。

(4)根据式（8）得到每个粗粒化序列的PE 值，即MPE值[9]。

2 PSO-PNN故障诊断模型

概率神经网络（PNN）是径向基神经网络的一种，PNN分类能力比较强、结构简单，容易设计算法，在模式分类问题中有比较广泛的应用。平滑因子是概率神经网络中最重要的参数，在目前的PNN 中，难以提炼出能反映整个样本空间的平滑因子，因此会影响诊断模型的准确性和快速性。当前的平滑因子基于有限的样本聚类方法或经验估计得到，此类方法难以完全表达样本空间的概率特性。平滑因子对概率神经网络的网络性能有着至关重要的作用，合适的平滑因子能显著提高概率神经网络的准确性和快速性，所以对平滑因子的优化是很有必要的。

粒子群算法（PSO）是一种基于群体的随机优化算法，它通过对鸟类捕食行为的研究来模拟人类社会中的情况。将鸟类捕食的飞行空间比作问题求解的搜寻范围，鸟群中的每一只鸟就代表一个可能产生的解，即粒子，每个粒子自身都具有速度和位置向量以及由适应度函数所决定的适应度值。本文的适应度函数是训练样本真实值和预测值的误差平方和，粒子在空间内不断通过式(9)、式(10)更新自身的速度和位置，直至寻找到最优解[10]。

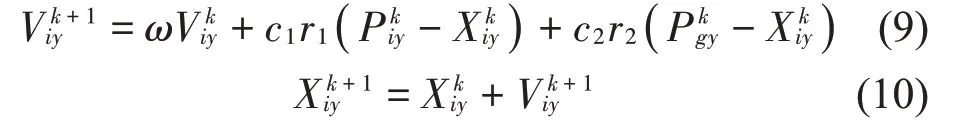
通过粒子群算法对概率神经网络中平滑因子进行优化，求解平滑因子的最优解。基于粒子群算法优化平滑因子求解最优解的流程图如图1所示。

图1 粒子群算法优化平滑因子流程图

3 实验分析

基于VMD、多尺度排列熵与PSO-PNN 故障诊断模型，具体实验步骤为：(1)提取轴承滚子故障、内圈故障、外圈故障状态和正常状态下的振动信号各60 组；(2)对提取的振动信号进行变分模态分解，得到k个模态函数，计算每一个模态函数的能量Ei(i=1,2,…,k)，构建能量特征向量T=[E1,E2,…,Ei](i=1,2,…,k)。根据构建的特征向量计算每个模态分量的多尺度排列熵的平均值MPEi(i=1,2,…,k)，构建特征向量S=[MPE1,MPE2,…,MPEi](i=1,2,…,k)；(3)将计算得到的特征向量输入到PSO-PNN故障诊断模型中，判断故障类型。

3.1 滚动轴承振动数据提取

实验数据主要通过江苏千鹏诊断工程有限公司设计的QPZZ-II 故障模拟平台进行采集，故障模拟平台如图2所示。

图2 QPZZ-II故障模拟平台

QPZZ-II故障模拟平台主要由变速驱动电机、信号采集系统、轴承、调速器、齿轮箱和轴组成，轴承的型号为N250，故障直径为0.176 mm，转速设置为1 750 r/min，采样频率设置为12 kHz。分别采集正常状态、外圈故障、滚子故障和内圈故障状态下的轴承振动信号各60组，采样点长度设置为4 096。内圈故障、外圈故障、滚子故障状态和正常状态下的原始信号时域波形图如图3至图6所示。

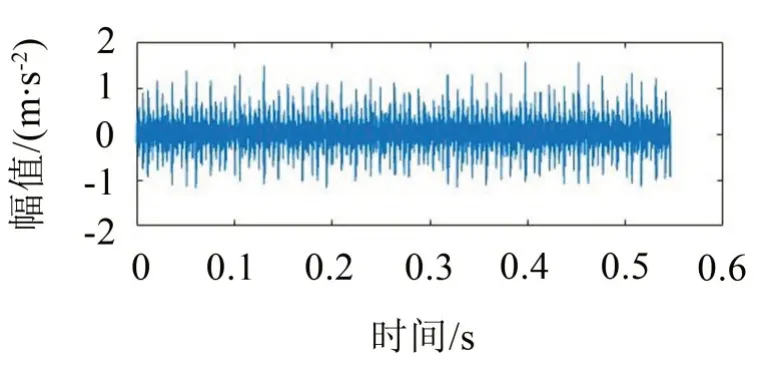
图3 内圈故障时域波形图

图4 外圈故障时域波形图

图5 滚子故障时域波形图

图6 正常状态时域波形图

3.2 基于VMD与MPE提取故障特征

采用VMD 方法分解之前需设定模态分解个数K的值，若K值较小时会出现重要原始信号丢失问题，若K值较大则会出现过分解问题[11]。本文主要通过观察各个模态中心频率来确定K的取值，以内圈故障为例进行分解，表1展示了不同K值对应的模态中心频率。通过表1可知当K=5 时，第4 和第5模态中心频率接近，由此可以推断产生过分解，因此确定K=4。

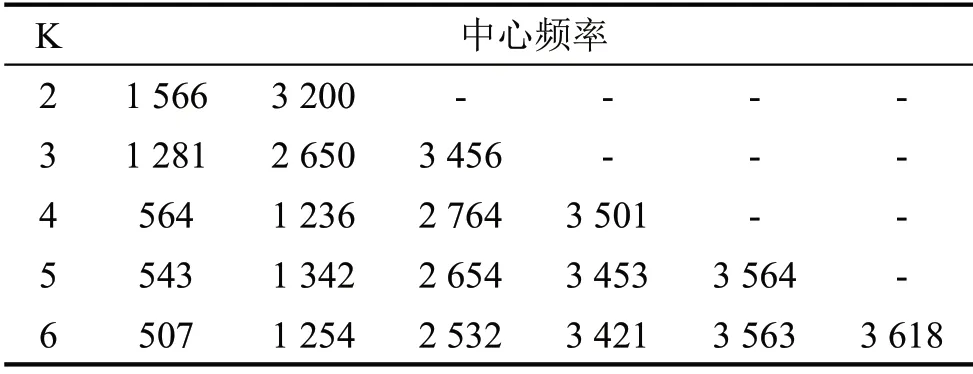
表1 不同K值对应的模态中心频率/Hz

内圈故障、外圈故障、滚子故障状态和正常状态的频谱图如7至图10所示。

图7 内圈故障频谱图

图8 外圈故障频谱图

由图7至图10可以看出当K=4 时，对于每种状态分解得到4个模态中心频率分别处于不同的频段并且未发生过分解现象。

计算多尺度排列熵时需设置延迟时间τ、尺度因子s、嵌入维数m。延迟时间对算法影响较小，一般设置τ=1。尺度因子一般设置为s≥10，滚动轴承4种状态的MPE值如图11所示。

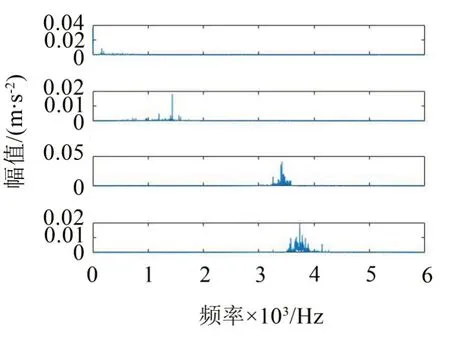
图9 滚子故障频谱图

图10 正常状态频谱图

图11 滚动轴承4种状态的MPE

由图11可以看出当s=12 时4 种状态的PE 值开始出现重叠，无法反映出多尺度排列熵的表征特性，故设置s=11。当s=1 时，可以区分正常状态和故障状态，基于单一尺度排列熵可以检测轴承故障但是无法进一步区分故障类型，若要具体检测出故障类型还需要更多的信息。在单一尺度下4 种类型PE值的大小关系为：外圈故障＞滚子故障＞内圈故障＞正常状态，当s＞9时这种数量关系不再成立，因此单一尺度的排列熵无法包含完整的故障信息，其它多个尺度也含有故障信息。嵌入维数通常设置为5～7，分析当嵌入维数为5～7 时的PE 值，如图12至图14所示。

1981年，调水入洪泽湖的时间有34个旬，基本覆盖全年，入洪泽湖泵站装机利用小时为7 500 h，入湖平均流量为385 m3/s；调水出洪泽湖的时间有31个旬，主要在7月中旬—9月上旬、10月—6月上旬，出洪泽湖泵站装机利用小时为6 700 h，出湖平均流量为266 m3/s。

如图12所示，当m=5时由于无法提取检测突变信号导致提取信息太少，如图13所示，当m=7 时间序列出现均匀化，无法反应时间序列的细微变化，故设置m=6。

图12 嵌入维数=5

图13 嵌入维数=6

图14 嵌入维数=7

3.3 基于PSO-PNN故障诊断

初始化参数时，在粒子群算法中设置加速度因子c1=1.494 45,c2=1.494 45，初始种群规模设置为50，迭代次数设置为200。通过粒子群算法优化平滑因子，得到平滑因子σ的最优解为1.5。

采集的滚子故障、内圈故障、外圈故障状态和正常状态下各60 组振动信号的1 至30 组作为训练样本，31 至60 组作为测试样本。将通过VMD 得到的能量特征向量和通过VMD-MPE得到能量特征向量分别输入到PSO-PNN故障诊断模型中，其结果如图15和图16所示。其中横坐标1至30为滚子故障、31至60 为内圈故障、61 至90 为外圈故障、91 至120 为正常状态，纵坐标1表示滚子故障、2表示内圈故障、3表示外圈故障、4表示正常状态。

图15 基于VMD与PSO-PNN模型诊断结果图

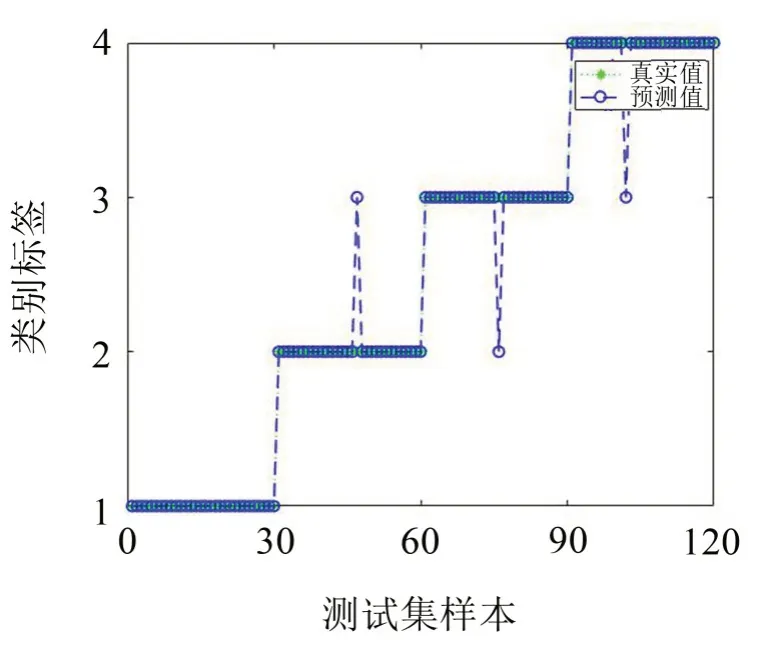
图16 基于VMD+MPE与PSO-PNN模型诊断结果图

3.4 实验结果

将通过VMD 得到的故障特征向量作为输入样本时滚动轴承故障诊断正确率为94.16 %（113/120），将基于VMD-MPE 得到的故障特征向量作为输入样本时滚动轴承故障诊断正确率为97.50 %（117/120），4 种故障类型具体的诊断结果正确率如表2所示。

从实验验证角度来说，将通过VMD-MPE 方法提取的故障特征作为故障诊断的输入样本时故障诊断准确率要高于将只通过VMD 方法提取的特征向量作为输入样本时的准确率，说明基于VMD-MPE方法提取故障特征向量具有较好的效果，可使故障诊断的准确率得到进一步提高。

表2 4种故障类型诊断的正确率

4 结语

针对滚动轴承的故障特诊提取与识别，提出基于VMD 和MPE 的PSO-PNN 滚动轴承故障诊断模型。通过变分模态分解将原始振动信号分解成K个包含故障信息的模态分量，通过MPE方法进一步量化各个模态分量所包含的故障信息，以实现滚动轴承故障特征的提取。将通过VMD与MPE方法得到的能量特征向量作为PSO-PNN 故障诊断模型的输入样本。将VMD-MPE 加PSO-PNN 方法与VMDPSO加PNN方法对比，可以看出VMD-MPE加PSOPNN方法可进一步提高故障诊断的准确率。