含Lugre动摩擦及间隙的振动系统的动力学分析
2019-12-27张艳龙李振国
张艳龙,李振国,王 丽
(1.兰州交通大学 机电工程学院,兰州730070; 2.兰州城市学院 数学学院,兰州730030)
含间隙的机械构件广泛存在于交通、航天、航空等机械系统中,在这类机械构件运转过程中或其他外激励作用下,一些零部件间将出现碰撞和摩擦,并引起噪声、振动等,将会更进一步导致效率降低甚至设备的损坏。因此多年来许多国内外学者通过建立不同的力学模型和摩擦模型来研究摩擦导致的黏滑、颤振及分岔行为。文献[1-2]利用含有干摩擦的Filippov 振动系统来研究滑移分岔和混沌动力学行为。文献[3]研究一种具有库伦干摩擦的振动驱动系统,分析其双参数分岔问题,并解释了滑移、黏滞等运动状态之间的转换,利用系统的黏特性对系统进行了优化。文献[4]建立一类含单边约束的2自由度塑性碰撞振动系统,研究参数变化、分段特性和擦边奇异性对系统的影响,分析了颤振碰撞发生的条件以及不同周期运动下的颤振运动现象。文献[5]通过研究三模块振动系统,分析非对称库仑干摩擦模型对振动驱动机械系统动力学行为的影响。周鹏等[6]建立干摩擦条件下含双侧约束的2 自由度塑性碰撞振动系统动力学模型,研究系统中存在的黏滑、滑动及碰撞等动力学行为。钱大帅等[7]利用谐波平衡法研究干摩擦振子双黏着运动响应的级数解并对黏滑边界进行了分析。丁旺才等[8]通过对含对称间隙的摩擦振子的非线性动力学行为的研究,阐述了该系统在运动过程中存在的叉式分岔、对称运动及反对称运动等。上述文献皆通过考虑静摩擦模型或者相关的解析法来研究不同的含间隙及碰撞振动系统。
但在实际工况中,为了更加准确描述含摩擦系统的动力学行为,很多文献考虑在不同的含摩擦系统中引入本身就具有动力学特性的动摩擦模型来研究,比如Dankowicz 动摩擦模型[9-10]、Lugre 动摩擦模型[11-13]以及改进Lugre 动摩擦模型[14],这些动摩擦模型从微观方面去解释摩擦力,其摩擦力不仅与物体运动速度和正压力有关,还和运动物体与接触面之间的内部变量(如两物体接触表面的平均形变)有关。为了研究滚子轴承实际工作过程中的动力学特性,将引入Lugre动摩擦模型(既可描述摩擦过程中的静态特性,也可描述其动态特性),来研究简化出的含摩擦及间隙的两自由度碰撞振动系统,并对该系统各个运动阶段进行理论分析,通过数值仿真分析,研究系统运动过程中由于间隙碰撞及摩擦引起的颤振等非线性动力学特性对系统稳定性的影响,从而为系统安全可靠性及相关机械构件的优化设计等提供相关的理论基础。
1 系统模型及运动状态

图1 单列圆柱滚子结构示意图
圆柱滚子在运转过程中会与保持架中滚子所处的隔离块两侧发生碰撞,从而产生颤振等动力学行为。为研究其运转过程中发生的碰撞及颤振等动力学特性,将该单列圆柱滚子轴承力学模型简化为一类含摩擦及间隙的两自由度碰撞振动系统,如图2所示。
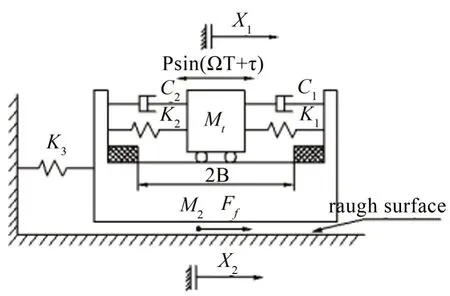
图2 含摩擦及间隙碰振系统模型简图
其中滚子用质量为M1的振子1表示。保持架的部分用质量为M2的振子2 表示,将隔离块两侧和保持架及阻尼油分别简化为相连的刚度系数为K1、K2和K3的线性弹簧及阻尼系数为C1、C2的线性阻尼器,振子1 与振子2 之间为光滑接触,振子2 与固定面之间为非光滑接触,假设阻尼是Rayleigh 型比例阻尼,碰撞过程由碰撞恢复系数R确定,简谐激振力Psin(ΩT+τ)作用在振子M1上,振子M1和振子M2的位移分别用X1和X2表示。
系统运动微分方程为
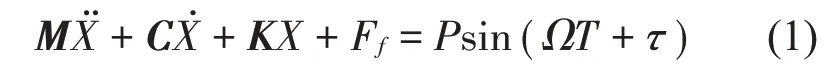
式中:
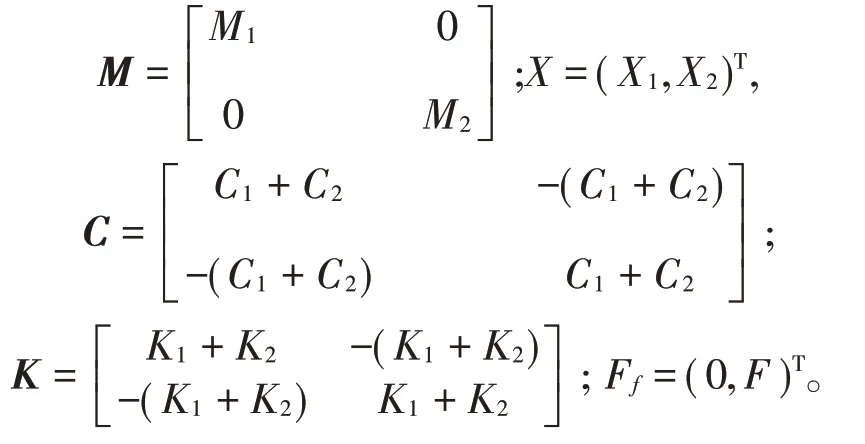
无量纲后的系统参数及变量如下
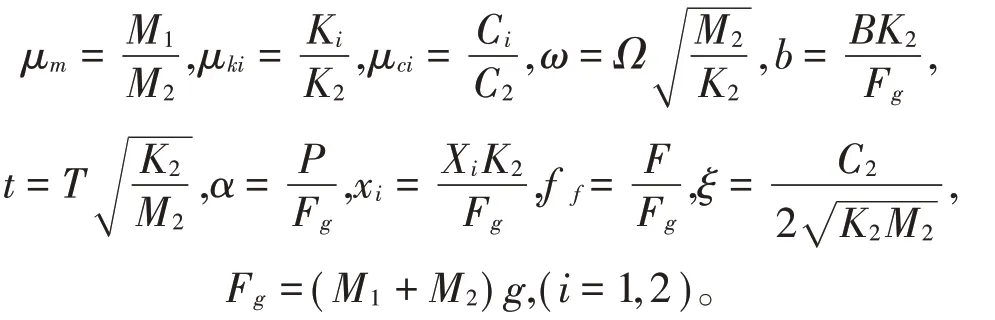
有学者认为在微观状态下,两个相互接触物体的接触面通过弹性刚毛接触,通过切向力作用,使得接触面间的刚毛发生形变而产生相应的摩擦力,当该弹性形变达到一定程度时,两个物体就会发生相对运动。
半个学年过去了,我是越战越勇,名次上升很快,甚至数学还以满分和张绍凡并驾齐驱。她看我的眼神变得不一样了,有惊奇还有疑惑。
无量纲后Lugre摩擦模型的数学描述为
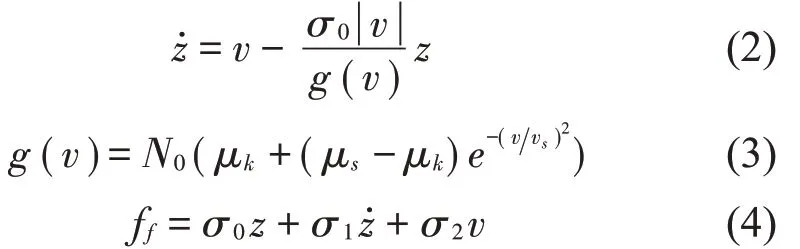
式中:无量纲量z表示刚毛平均形变;v表示接触面相对速度;N0表示正压力;vs表示Stribeck速度;μs表示静摩擦系数;μk表示最小动摩擦系数;σ0、σ1、σ2分别表示刚度系数、阻尼系数和黏滞系数;ff为摩擦力。
在完整的系统运动过程中,将产生3 种不同性质的运动状态:
(1)振子1 和振子2 同时处于运动状态,即滑移阶段;
(2)振子1 处于运动状态,振子2 处于粘着静止状态;
(3)由于两侧存在约束,当振子1 与振子2 的位移差等于间隙b时,两者发生碰撞,即碰撞阶段。
可见,振子2的将会在滑移、粘着与碰撞三者运动状态之间相互转换,这使得其运动过程变得较为复杂。现将该系统的运动过程划分为如下阶段进行讨论:
阶段1:滑移段
因为有简谐激励力作用在振子1上,故振子1的状态始终是运动的,而振子2 所受的力则为通过振子1 作用在振子2 上的力,该力为振子2 的驱动力,即若振子2 受到的力大于振子2 所受弹簧3 的弹性力以及摩擦力,且同时振子2的速度不为零,即时,则 振子2 做加速滑移运动,即前滑段。此时,振子1 与振子2都处于运动状态,系统运动状态方程为
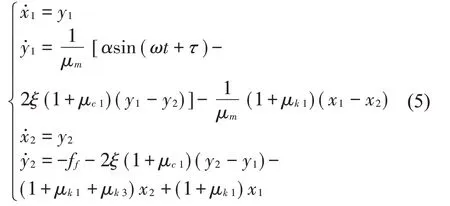
若振子2 所受到的力小于振子2 所受的弹簧3的弹性力及摩擦力,且同时振子2的速度不为零,即时,则振子2 做减速滑移运动,即后滑段。此时,振子1 与振子2都处于运动状态,系统运动状态方程为
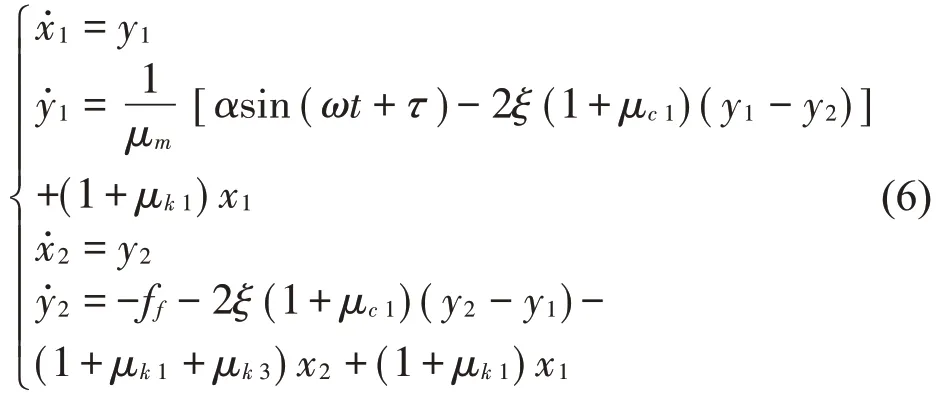
阶段2:粘着段
若满足振子2 所受到的力小于振子2 所受弹性力及摩擦力,且同时振子2 的速度为零,即时,则振子2处于黏滞状态。此时,振子1为运动状态,振子2为黏滞状态,系统运动状态方程为
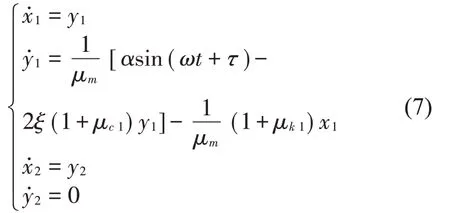
阶段3:碰撞段
由于摩擦力的作用,系统在粘着状态下不会发生碰撞,而在滑动状态时,当振子1 与振子2 的位移满足 ||x1-x2=b,则此时振子1 与振子2 发生碰撞,根据动量守恒定律及碰撞关系得
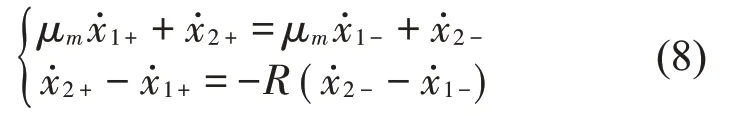
通过数值模拟对综上所述的含间隙及摩擦的碰撞-振动系统的3 种运动阶段进行动力学分析,由于对称刚性约束碰撞振动系统在适当的系统参数条件下能够呈现对称型1-1-1周期运动,这里用n-p-q表示系统的周期碰撞运动,n表示力周期数,p和q分别表示振子1 与振子2 在挡板A 和C 的碰撞次数。为了研究摩擦碰撞振动系统的周期运动及分岔现象,选取Poincaré 截面建立Poincaré映射:
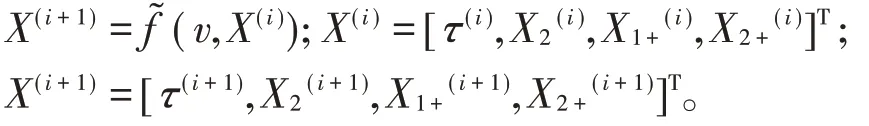
式中:X∈R4;v是实参数。
2 激振频率对系统动力学行为的影响
事先通过选取多组系统参数对系统的动力学行为进行大量的数值仿真,发现选取如下系统参数:M1=0.1kg,M2=1.0 kg,K1=K2=4.44 N/m,K3=6.68 N/m,C1=C2=0.25 N ⋅s/m,ξ=0.5,vs=0.15,σ0=2 500,b=0.2,R=0.8,α=3.2,μk=0.5,μs=0.25,σ1=100,σ2=10,系统存在特定的分岔行为,如图3所示。
进而分析Lugre 动摩擦对系统动力学行为的影响,由图3可见随着频率ω的增大,系统总在混沌状态与逆周期倍化分岔状态之间相互转换,在ω=12.77时,系统发生Hopf分岔,最后在ω>13.34时,系统进入周期1稳定状态。
图4为系统在激振频率ω取不同值时的相图和时间历程图。如图4(a)所示,当ω=13.34 时,系统呈现出非对称的周期1-1-1 运动,随着激振频率的减小,系统从稳定的周期1 运动进入混沌状态;在ω=7.0时,系统从混沌状态进入周期1-2-2运动,相图如4(b)所示,随后又进入混沌状态;当激振频率减小到ω=5.1 时,系统进入周期1-3-3 运动,相图如4(c)所示,在ω=4.9时,系统发生倍化分岔,随后随着激振频率的递减,系统又进入混沌状态;当ω=4.0 时,系统又进入周期1-4-4 运动,相图如4(d)所示,在ω=3.85时,系统又发生倍化分岔;随着激振频率的不断递减,系统在ω=3.3 和ω=2.7 时,分别由混沌状态进入周期1-4-4运动和周期1-5-5运动,相图如图4(e)和图4(f)所示,在ω变化期间,系统又经历了由混沌状态到倍化分岔以及由倍化分岔再到混沌状态的改变。图4(g)至图4(h)所示的ω=13.34 时的时间历程图详细描述了系统的运动过程。以碰撞前A点为起始点进行分析,系统开始由A点进入到碰撞阶段,碰撞瞬间完成,速度发生突变,但位移未发生改变,到B点碰撞阶段结束;此时系统由B点进入后滑段,速度逐渐降低,此时摩擦力小于驱动力,在CD段发生粘滑现象,速度、位移基本未发生变化;随着力方向的变化,在驱动力大于摩擦力的瞬间,速度发生突变,但速度突变幅值较小,接近平滑过渡,E 点为粘滑现象结束点;此后由于系统受力方向和速度方向一致,因此在E 点进入前滑段,在F 点发生碰撞,前滑段结束,速度发生跳跃,G点为碰撞结束点,在GA段,由于力方向和速度方向的不断变化,系统先进入后滑段,接着过渡到前滑段,到A点完成系统的一个周期运动。由于AB段为碰撞段,速度发生跳跃,但位移未发生改变,故在图4(h)所示的位移-时间历程图中,A、B点是重合的,同理,E、F点也是重合的。
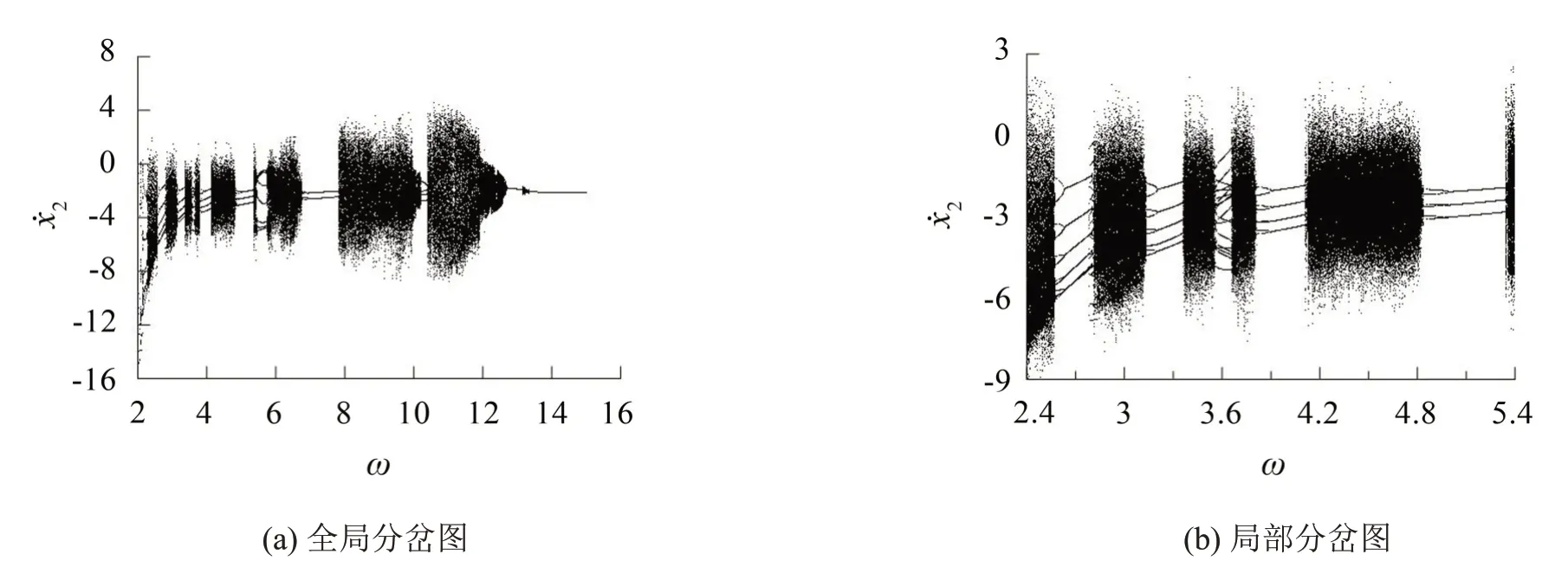
图3 系统随量纲-激振频率的分岔图
3 间隙对系统动力学行为的影响
选取大量参数进行数值仿真分析,为更加明显表现系统的动力学特性,现选取系统参数如下:
M1=0.1kg,M2=1.0 kg,K1=K2=4.44 N/m,C1=C2=0.25 N ⋅s/m,K3=6.68 N/m,ξ=0.5,vs=0.15,σ0=3 000,ω=2.2,R=0.5,α=3.2,μk=0.5,μs=0.55,σ1=500,σ2=10。对该系统进行数值模拟,以滚子与隔离块之间的间隙b作为分岔参数,分析其对系统动力学行为的影响,得到系统在不同激振频率下的分岔图如图5所示,其中图5(a)是当激振频率ω=2.2时,得到的系统全局分岔图,从图中可以看出随着间隙b的增大,系统由原先的混沌状态逐渐进入逆周期倍化分岔状态,同时在不断的递增过程中,又再次进入混沌状态系统,随后又发生逆周期倍化分岔以及后面的Hopf分岔,同时系统的运动周期也在逐渐减小;图5(b)为图5(a)的局部放大分岔图,该图可以更加清楚显示系统在ω=2.2 时的分岔状态。图5(c)至图5(d)分别为激振频率ω=5.0 和ω=8.0 时的系统分岔图,结合ω=2.2 时的分岔图,可以看出将间隙b控制在一定的范围内时,随着激振频率ω的增加,系统的运动周期会越来越小,直至最后的周期1 运动状态。
4 结语
本文建立一类两自由度含间隙及摩擦碰撞振动的系统动力学模型,根据实际情况,详细分析了该系统的整个运动过程,列出系统在不同运动阶段的判断依据,并利用数值仿真分析了Lugre 动摩擦模型对系统动力学行为的影响,为该类系统的参数优化及稳定性分析提供一定的理论依据。
(1)当激振频率较小时,系统的分岔现象较为明显,存在较多的运动周期,系统的动力学行为变得较为复杂,随着激振频率的递增,系统的运动周期现象逐渐减小,直至进入稳定的周期1运动状态。
(2)当激振频率与间隙均较小时,系统的动力学行为较为复杂,总在混沌运动状态和逆周期倍化分岔状态之间变化,存在多周期运动状态,运动过程较为复杂。但若将间隙控制在一定的范围内时,随着激振频率的增加,系统的运动周期会越来越小,动力学行为也变得不再复杂。
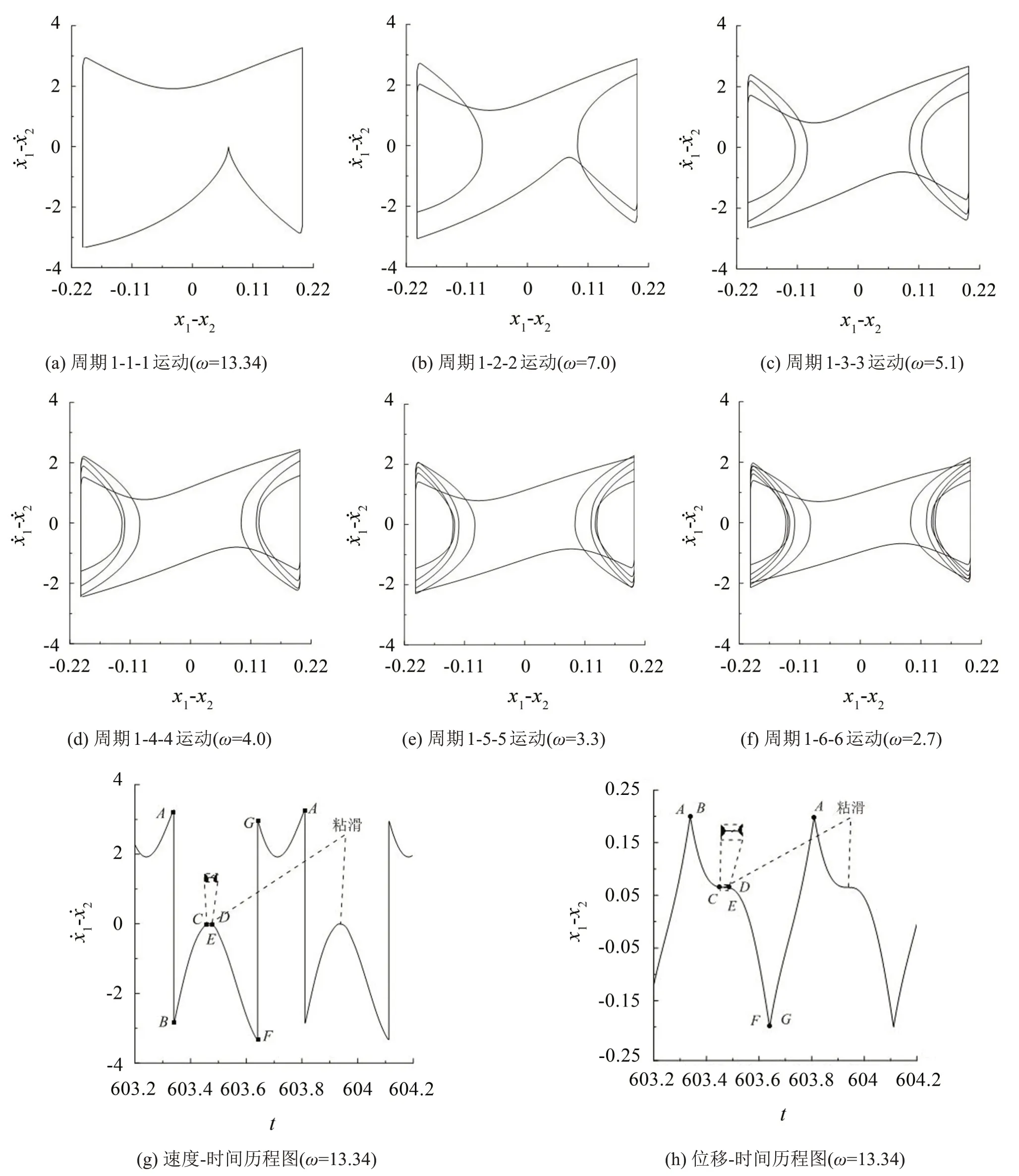
图4 系统运动相图和时间历程图
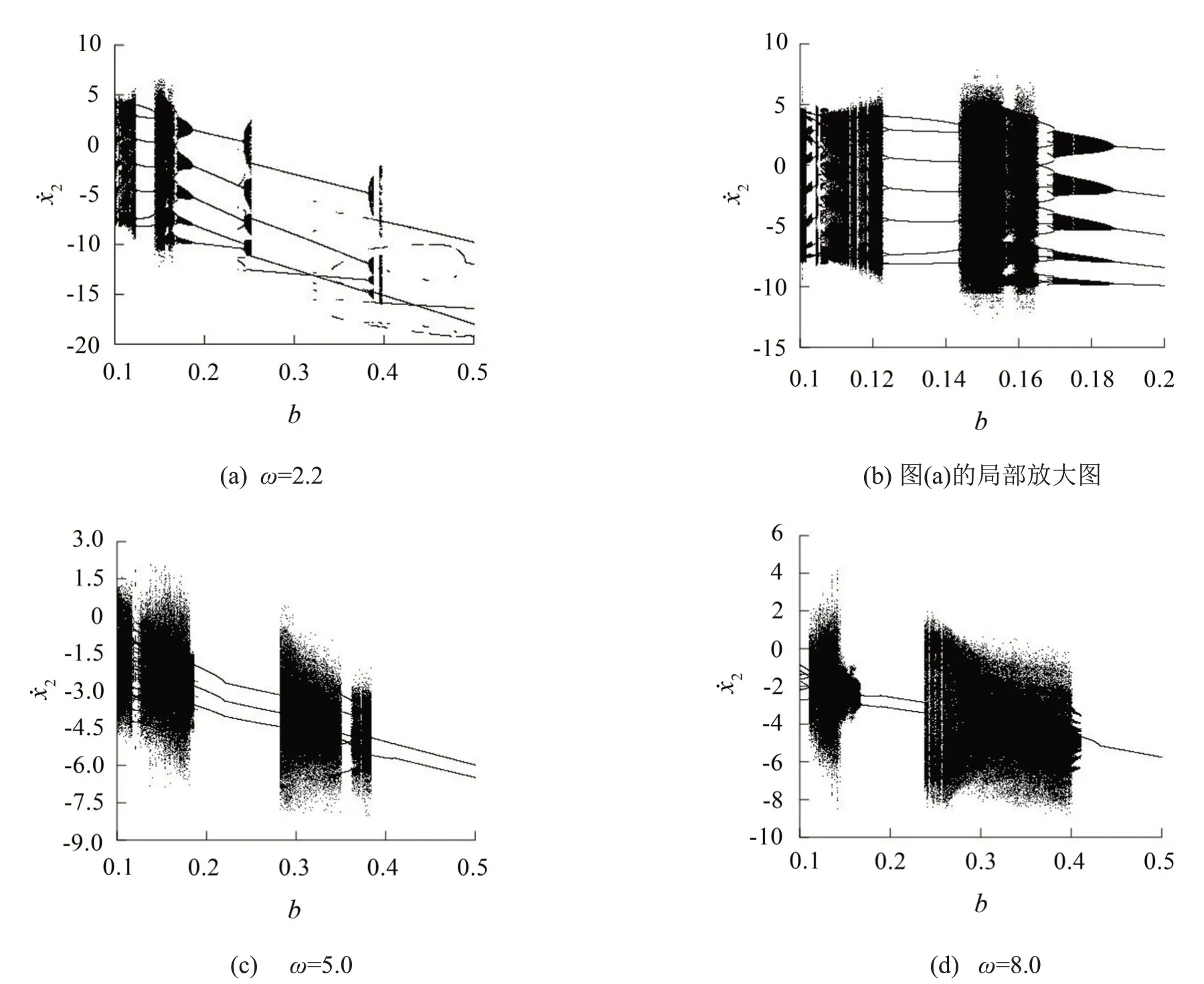
图5 系统随间隙变化的分岔图
