一种未知激励下土木工程结构模态参数识别新方法
2019-12-27刘景良俞安华骆勇鹏
刘景良,俞安华,吴 琛,盛 叶,骆勇鹏
(1.福建农林大学 交通与土木工程学院,福州350002;2. 福建工程学院 土木工程学院,福州350118)
模态参数识别是结构健康监测领域的一个关键问题。通过模态参数可以获得结构的动力特性,从而方便对结构进行进一步的振动控制和状态评估[1-3]。然而需要指出的是:在实际工程中结构受到的激励是难以测量的,只有输出响应才能测得并提供有用的信息。因此,对未知激励下的结构模态参数进行识别研究具有十分重要的意义。
目前,信号处理技术在结构模态参数识别研究领域获得广泛运用,主要方法有峰值采样法、频域分解法[4]、随机子空间[5]、频响函数[6]、自然激励技术[7]、特征系统实现算法[8]和自回归滑动平均[9]等。然而,上述识别方法的可靠性容易因噪声的影响而降低,同时它也不能识别土木工程结构中常见的密集模态参数[10]。为此,一些新的时频分析方法不断被引入并成为处理未知激励下土木工程结构随机响应信号的有力工具,其主要方法有Wigner-Ville 分布、短时傅里叶变换、小波变换(Wavelet Transform,简称WT)、希尔伯特-黄变换(Hilbert-Huang Transform,简称HHT)等,而其中又以HHT和WT方法研究最为深入[11-12]。
然而由于环境噪声的不可避免性,WT 需要对信号进行多重分解才能有效揭示信号的内部特征,因而其无法很好地分析大型土木工程结构的响应信号[13]。基于经验模态分解(Empirical Mode Decomposition,简称EMD)的HHT 方法通过三次样条插值将多分量信号自适应地分解成一系列本征函数,但EMD本质上是一种经验性的局域分析方法,它无法分离密集的模态响应,特别是具有模态频率叠混现象的多分量信号[14]。Wu 等[15]基于高斯白噪声统计特性,提出集合经验模态分解方法来解决EMD算法中存在的模态叠混问题。该方法通过添加高斯白噪声对数据的极值分布进行均匀化,从而缓解了模态密集和叠混现象。但正是由于白噪声的添加,集合经验模态分解算法也将出现分解不完备性和重构信号中含有白噪声等缺点[16]。为此,Chen 和Wang[17]提出解析模态分解(Analytical Modal Decomposition,简称AMD)这一时域信号分解方法来提取分量信号。该方法的本质是利用构造的正交函数与原始信号乘积的希尔伯特变换把每一具有特定频率成分的分量信号解析地分解出来。AMD 不但能够从大的波动中分离出小的间歇性波动信号,同时也能够分解密集模态分量和窄带分量信号。然而需要指出的是:模态参数时域识别法的关键是如何获得结构的自由衰减振动响应。而随机减量法(random decrement technique,简称RDT)作为一种从随机振动响应中提取自由衰减振动信号的时域数据预处理方法,能够在多分量信号分解之前对振动信号进行处理从而有效减少信号中的随机成分。
在采用AMD分解出分量信号后,提取瞬时频率等模态参数成为可能。常见的方法有希尔伯特变换(Hilbert Transform,简称HT)、零点法和Teager 能量算子等,而其中又以HT 最为普遍和直接[18]。但是HT对噪声极为敏感,其识别的结果与真实值存在一定的偏差,因此有必要引入卡尔曼滤波(Kalman Filter,简称KF)等平滑算法来修正HT识别的模态参数结果。
基于此,本文从未知激励下的结构振动响应信号出发,联合RDT、AMD、HT和KF方法提出了一种新的未知激励下的土木工程结构模态参数识别方法,并通过一个合成信号和一个4 层钢框架结构试验验证了该方法的有效性。研究结果表明:该方法能够准确有效地识别结构的固有频率和阻尼比。
1 基本理论
新提出的未知激励下土木工程结构模态参数识别方法的流程图如图1所示。
该方法主要由以下3 个步骤组成。首先,采用RDT从实测的环境振动响应信号中估算出自由振动响应。其次,引入AMD 算法将估计出的自由振动响应信号分解成各阶独立的模态分量信号,且每阶频率对应一个自由振动的模态响应。最后,通过HT 得到各阶模态响应的固有频率和模态阻尼比,然后进一步运用KF 算法进行平滑处理,从而得到更为精确的频率值和阻尼比值。
1.1 采用RDT估计自由响应
由于未知激励下的响应信号是随机的,直接对原始响应进行分析是不合适的[19]。而由Cole 提出的随机减量技术主要用于提取随机振动信号的自由衰减响应[20]。RDT 基于这样一个假定:原始响应信号x(t)由确定性和随机性两部分组成。在合理地确定初始条件(阈值a)之后,可通过统计平均的方法将随机部分去除,从而过滤出确定性的自由衰减信号,如式(1)所示。
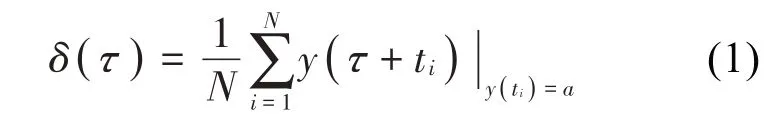
式中:y(ti)是实测原始响应信号x(t)在ti时刻处的样本个体,且y(ti)满足阈值a条件,如图2(a)所示。用y(ti)=a截样本曲线可得到若干个交点,其中N为交点的数量,τ为时间变量。通过选择合适的阈值可以得到足够的交点以便获得良好的自由响应估计值。因此,阈值a的选择对RDT至关重要,常见的阈值选定标准之一就是使估计的响应方差最小化,如式(2)所示。

图1 未知激励下土木工程结构模态参数识别新方法流程图

式中:σx是实测响应信号x(t)的标准差。为详细说明自由响应的估计过程,采用一个如式(3)所示的合成信号来模拟结构在未知激励下的随机响应。
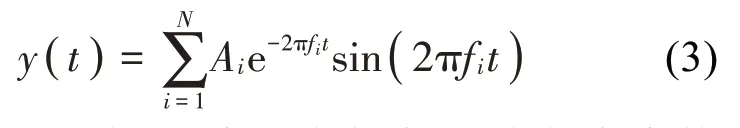
式中:Ai为振幅,fi为第i个固有频率,N为频率个数或模态阶数。设定合成信号含有4 阶频率,即f1=2 Hz,f2=4 Hz,f3=5 Hz 和f4=10 Hz;而对应的振幅分别为A1=7,A2=9,A3=2 和A4=5。采样时间和采样频率分别设为1.5 s 和100 Hz,共150 个样本。根据式(2)选定阈值,其交点如图2(a)中的虚线所示。由图2(a)可知,共有4 个交点,分别标记为1、2、3 和4。其中,每个交点对应特定的信号段,且信号的每一段(用图2(b)中的S1、S2、S3和S4标记)均由45个样本组成,即持续时间为0.45 秒。最终,根据RDT提取的自由振动响应如图2(b)中的实线所示。
1.2 AMD定理
在获得自由振动响应δ(t)之后,可采用AMD定理将其分解成多个单分量信号,且每一个分量信号xi(t)对应一个频率成分和独立模态,其表达式如式(4)所示。
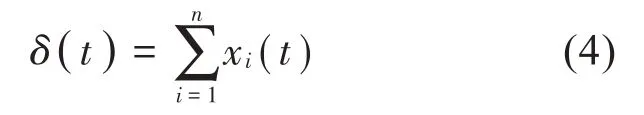
式中:n为分量信号个数。
对于任意由n个信号分量xi(t)(i=1,2,3,…,n)组成的原信号δ(t),如果它的每一分量的频率ω1、ω2、…、ωn(ωi>0;i=1,2,…,n)满足( |ω1|<ωb1),(ωb1< |ω2|<ωb2),…,(ωb(n-2)< |ωn-1|<ωb(n-1))和 (ωb(n-1)< |ωn-1|),其中:ωbi∈(ωi,ωi+1)(i=1,2,…,n-1)为n-1个二分截止频率,则它的每一信号分量可以解析地给出,如式(5)和式(6)所示。
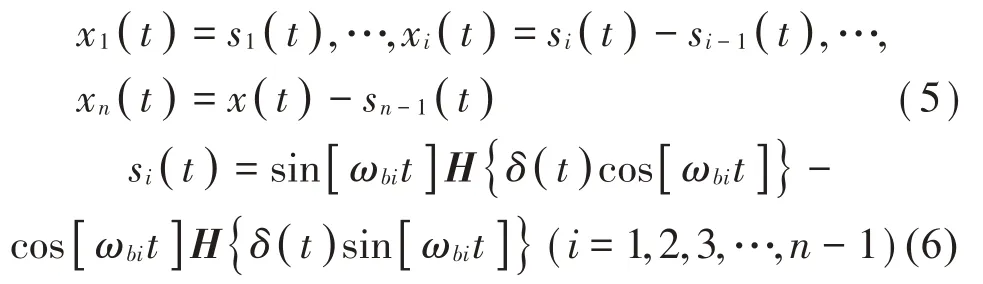
式中:H{∙}为Hilbert 变换。
1.3 模态参数估计
1.3.1 希尔伯特变换
在成功提取原始随机响应信号的分量信号后,采用HT求解每个单分量信号xi(t)的瞬时频率和瞬时阻尼比。HT通常被定义为信号的卷积,其表达式如式(7)所示[21]。
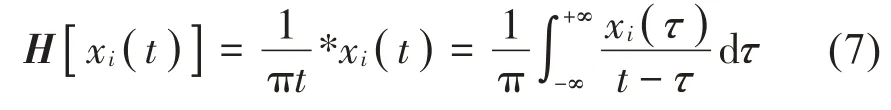
将xi(t)作为实部,其HT 变换作为虚部,构建新的解析信号xa(n)如下
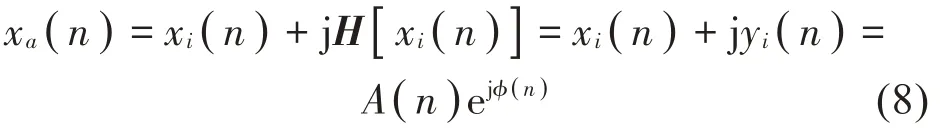
在构建解析信号之后,可通过式(9)和式(10)估计每个单分量的瞬时频率ω(n)和瞬时阻尼比ζ(n)。
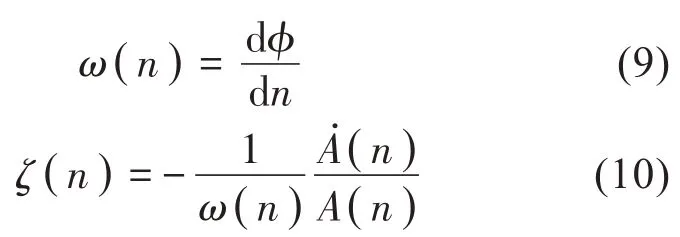
1.3.2 卡尔曼滤波
KF 是一种特殊类型的滤波器,常用于建模、跟踪、提取、滤波或平滑信号[22]。通过HT 和求导估计的信号频率和模态阻尼比通常都是时变和振荡的,这是因为任何轻微的扰动在经过求导后都有可能被放大从而引起模态参数识别的潜在误差。而KF 滤波算法可以最小化这种可能存在的误差,其基本原理如下
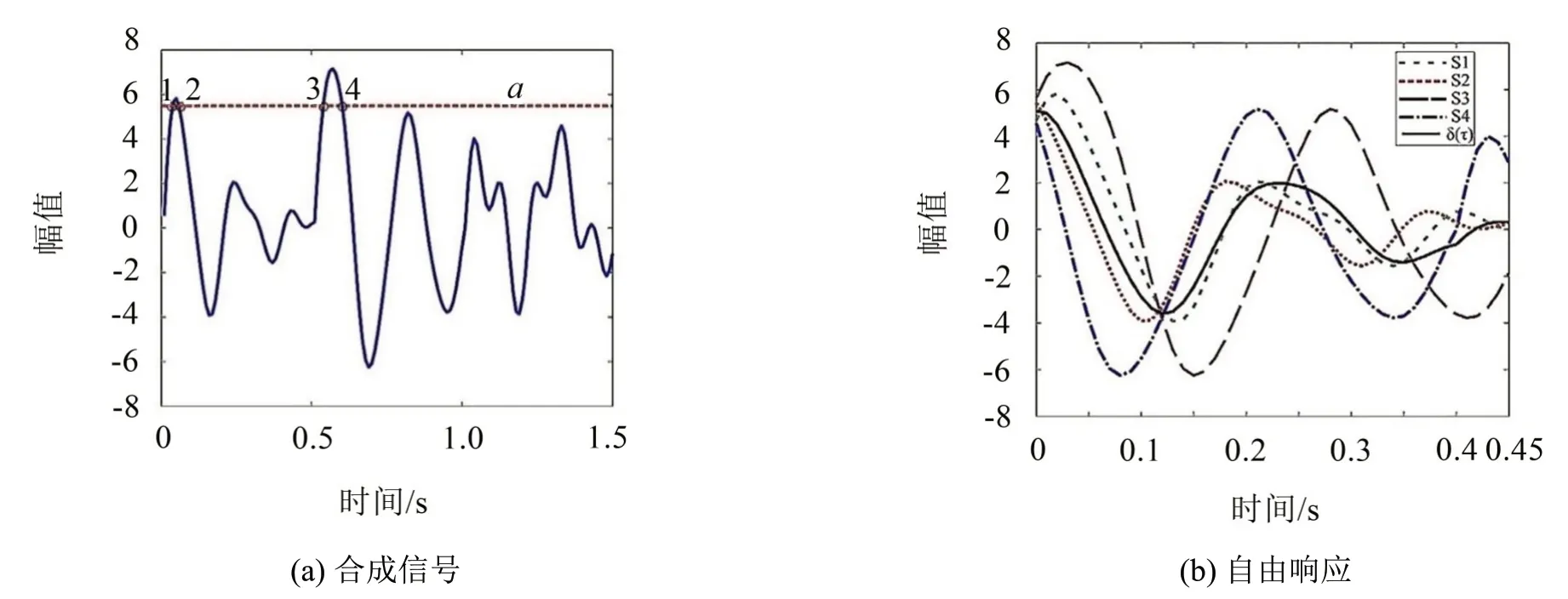
图2 RDT分析处理信号
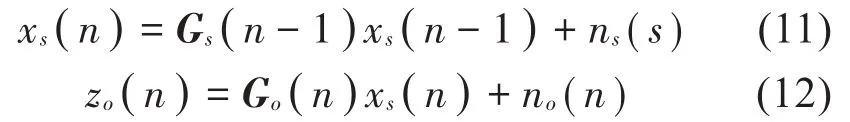
式中:xs和zo分别是状态和观测变量;Gs和Go分别为状态转移矩阵和观测矩阵;ns和no分别表示状态变量和观测变量的噪声。
为应用传统的KF,需进行如式(13)至式(17)所示的迭代过程。在此迭代过程中,状态变量xs由式(8)中的实部xi(n)与虚部yi(n)组成。
(1)第n次迭代时的预测状态变量xs(n)和预测协方差p(n)分别为
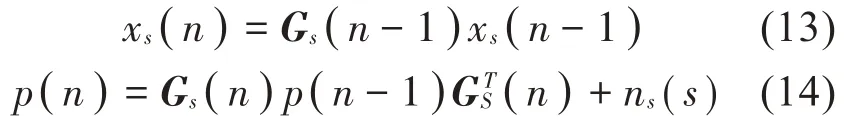
(2)获得新的KF的增益矩阵GKF
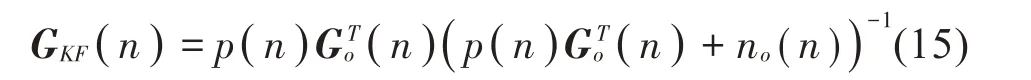
(3)根据计算得到的GKF和新的测量数据zo(n),预测样本xs(n+1 )和相应的误差协方差p(n+1 ),如式(16)和式(17)所示。
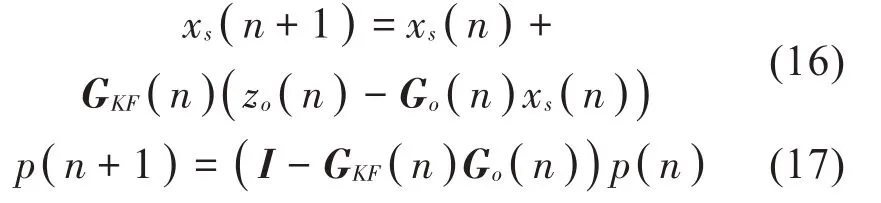
式中:I为单位矩阵。
通过KF 迭代过程可得到新的实部xi(n)和虚部yi(n),然后将其分别用于计算每个分量的瞬时振幅和瞬时相位φ(n)=从而最终估计得到更精确的固有频率和模态阻尼比。
2 数值模拟验证
为验证新方法的有效性,考虑如式(18)所示的合成响应信号。
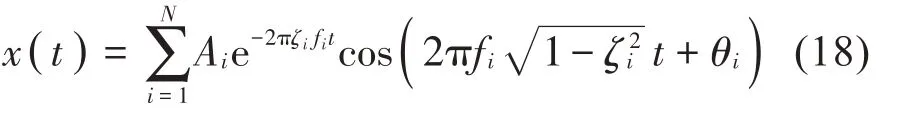
式中:Ai是振幅,fi是固有频率,θi是相位角,ζi是阻尼比,i代表模态阶数,N是频率的总个数。
设定合成信号由x1(t)、x2(t)和x3(t)3个分量信号组成,且3个分量信号的频率分别为f1=3Hz,f2=4 Hz,和f3=7 Hz。振幅Ai=1且初始相位θi=0,其中i=1,2,3。对应的阻尼比ζ1=0.8%,ζ2=1.0%和ζ3=0.5%。信号采样频率为200 Hz,采样时间为8 秒。由于所选合成信号中的2 阶模态频率(3 Hz和4 Hz)十分接近,因此可以用来验证所提出的方法能否有效分解密集模态分量信号。
模拟的合成信号如图3所示,由于其为自由衰减振动响应,因此无需运用RDT进行预处理。通过选择合适的截止频率,采用AMD定理分解得到的各阶自由振动响应如图4所示。
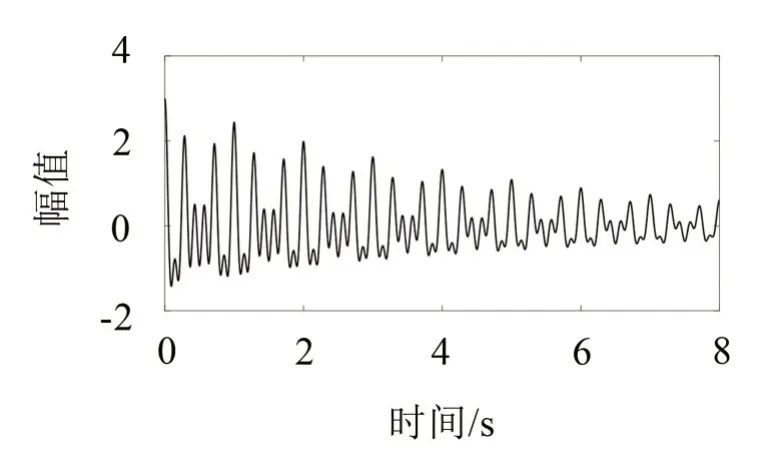
图3 模拟的合成信号
由图4可知,提取的各阶模态分量与真实值基本一致。通过HT 和KF 算法估计的合成信号各阶频率如图5所示。由图5可知,由于端点效应的影响,频率识别值在端点附近存在较大的起伏,但随后收敛于一个特定的值。同理,通过HT 和KF 算法估计的合成信号各阶阻尼比如图6所示。与频率识别值类似,阻尼比识别值在端点附近也存在较大的起伏,但随后也收敛于一个特定的值。从表1可以看出,固有频率识别结果与理论值十分吻合,特别是模态密集的两个分量信号的频率值(分别为3 Hz 和4 Hz)都得到了较好地识别。由此可见,阻尼比识别结果与理论值吻合较好,这很好地验证了本文所提方法的有效性和准确性。
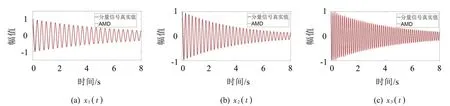
图4 基于AMD分解得到的各阶分量信号
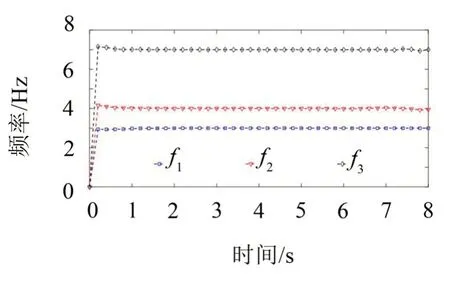
图5 HT-KF 估计的频率
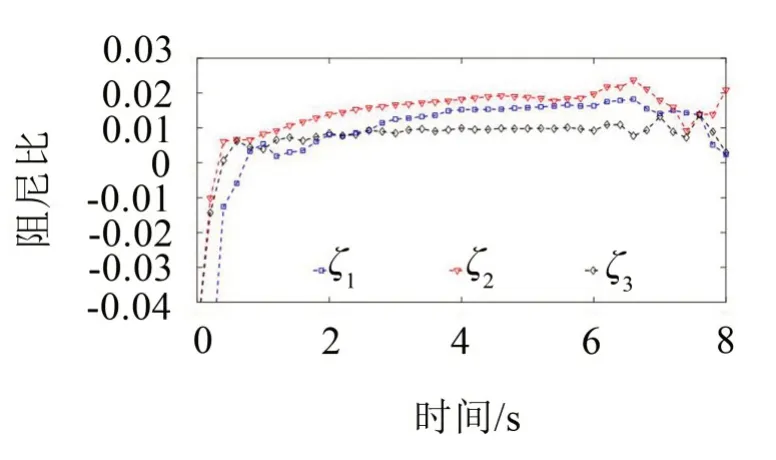
图6 HT-KF 估计的阻尼比
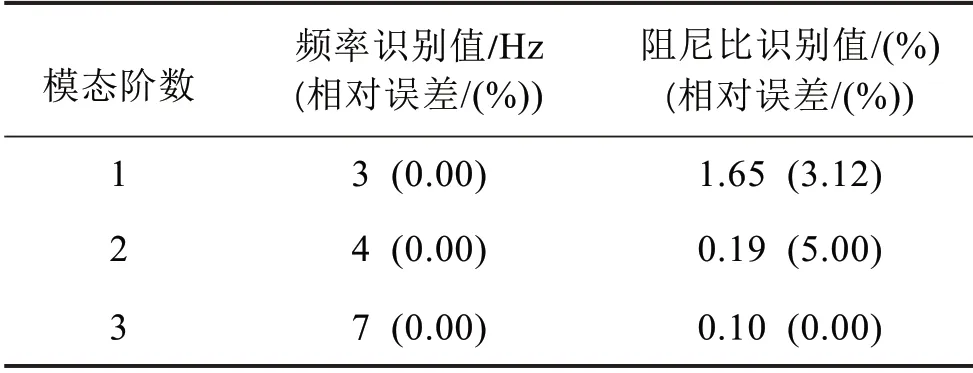
表1 合成信号固有频率和阻尼比识别值
3 试验验证
3.1 钢框架模型
通过一个钢框架结构动力试验来验证所提出的识别方法。图7所示为2 跨×1 跨的4 层钢框架缩尺模型,相应的数学简化模型如图8所示。梁柱轴间距为225 mm,各层层高均为225 mm。梁、柱材料均为碳素结构钢Q235,其界面尺寸和具体特性如表1所示。根据表1中的数据可求得结构各层质量为m1=m2=m3=4.02 kg,m4=3.48 kg,完整无损状态下结构各层理论刚度均为263 kN/m。在已知结构各层质量和刚度的前提下,可求解结构的1阶、2 阶、3 阶和4 阶固有频率理论值,分别为17.39 Hz、49.80 Hz、75.56 Hz、91.77 Hz。在试验过程中,利用支架上安装的激振器在结构顶层施加扫频激励,然后通过在结构第4 层布置的传感器测量其加速度响应信号,其中采样频率和采样时长分别为1 000 Hz和600秒。
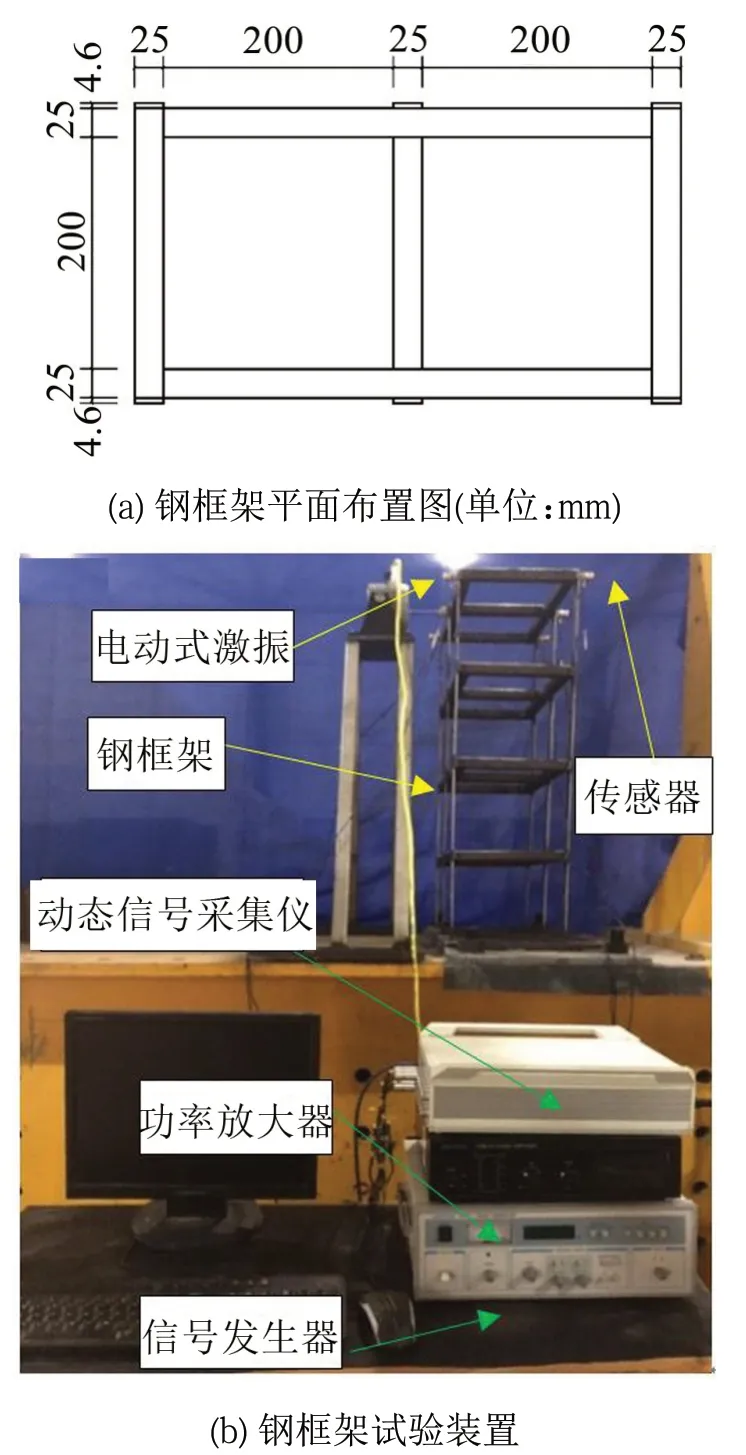
图7 缩尺钢框架结构模型
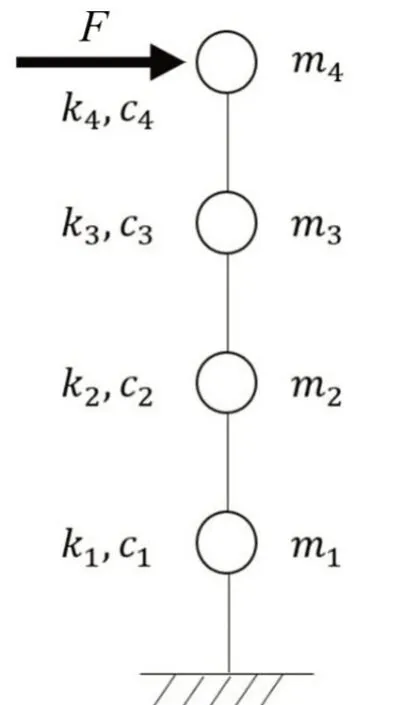
图8 结构简化数学模型
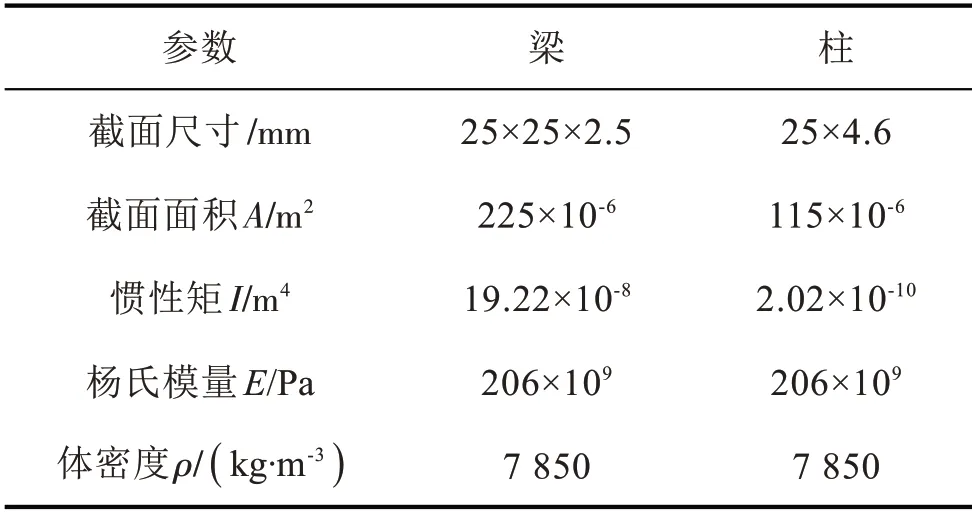
表2 结构构件特性
3.2 模型参数识别
实测的结构第4 层加速度响应信号如图9所示。首先,采用RDT 将第4 层加速度响应信号转换成自由振动响应信号,此时,时间被缩短为1.2 秒,共1 200 个样本,结果如图10所示。由图10可知,相比于原始信号,自由振动响应信号更加光滑,其受噪声干扰较少。通过选择合适的截止频率,采用AMD 定理分解自由振动响应信号从而得到如图11所示的各阶模态分量信号。采用HT 可初步估算出各阶模态分量信号的频率,但由于激励和求导运算的缘故上述频率估计值呈现振荡模式,因此需通过KF 对其进行光滑处理,其结果如图12所示。由图12可知,由于端点效应,频率识别值在端点附近存在较大的起伏,但随后收敛于一个特定的值。通过HT 和KF 算法估计的各阶模态分量信号的阻尼比值如图13所示。由于端点效应的缘故,阻尼比识别值在端点附近也存在较大的起伏,但随后收敛于一个特定的值。从表3也可以看出,前3 阶频率识别值与理论值吻合度较高,误差率分别为0.75 %、2.22 %和3.16 %。第4 阶的误差相对较大(误差率为6.76 %),这是由于试验材料自身的缺陷、焊接的影响等多种因素引起的。整体来说,频率识别值与理论值吻合度较好。通过动力试验实测得到的1、2、3 和4 阶阻尼比理论值分别为1.23 %、0.19 %、0.12 %、0.08 %,而1、2、3 和4 阶阻尼比识别值分别为1.26 %、0.20 %、0.13 %、0.07 %。由表3可知,阻尼比识别值与理论值吻合度较高,相对误差较小,这再次验证了本文所提方法的有效性和准确性。
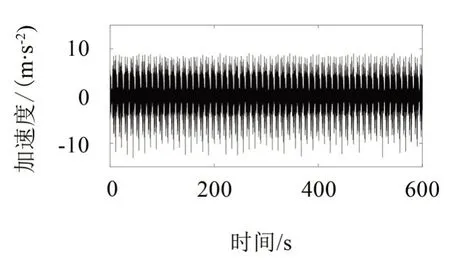
图9 第4层的响应信号
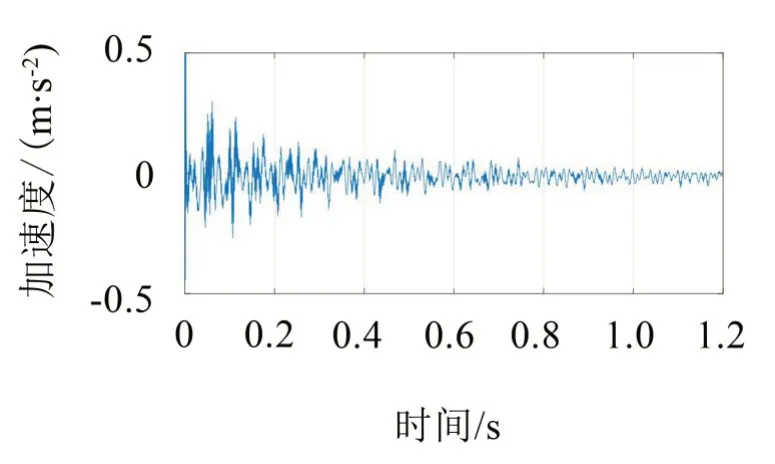
图10 基于RDT提取的自由响应信号
4 结语
结合随机减量技术、解析模态分解、希尔伯特变换和卡尔曼滤波理论提出了一种未知激励下土木工程结构模态参数识别新方法。通过一个含有密集模态分量信号的合成信号以及一个未知激励作用下4 层钢框架结构试验验证了提出的方法,主要结论如下:
(1)RDT 能有效地提取未知激励下的结构自由振动响应,同时消除一些测量过程中产生的噪声。
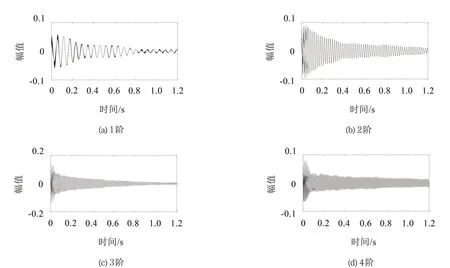
图11 基于AMD分解得到的各阶分量信号

表3 识别的钢框架固有频率和阻尼比
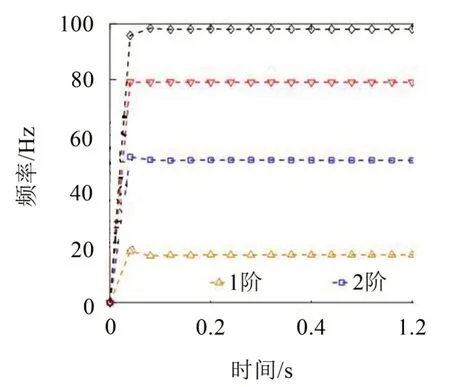
图12 基于HT-KF 估计的频率
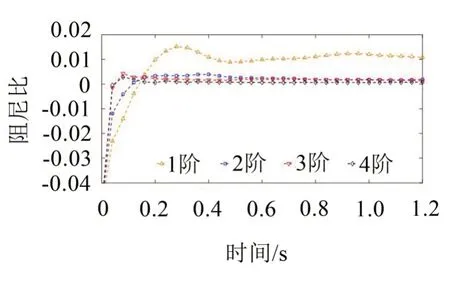
图13 基于HT-KF 估计的阻尼比
(2)AMD 能够分解含有密集模态分量的多分量信号,但是通过HT 和求导估计的分量信号的幅度和频率通常是时变和振荡的,而KF 滤波算法可以最小化这种可能存在的误差。
(3)基于RDT、AMD、HT 和KF 联合的模态参数识别方法能够准确有效地识别未知激励作用下4层钢框架结构的各阶频率和阻尼比,将来有可能应用于实际土木工程结构。
