功率分流式风电机增速箱振动特性分析
2019-12-27于印鑫
于印鑫,李 宽,郑 朋,李 诤
(1.昆明理工大学 机电工程学院,昆明650500;2.云南省高校振动与噪声重点实验室,昆明650500;3.大连华锐重工集团股份有限公司齿轮箱研究所,辽宁 大连116013)
大功率风机增速箱均以两级行星齿轮和一级平行轴齿轮的形式进行设计,但结构形式差别较大,由于行星齿轮传动系统自身结构及内部激励复杂,导致其早期失效频发,已成为制约其向长寿命和高可靠性应用发展的重要因素之一。故研究行星齿轮传动系统的激励、建模及振动响应特征,对提高和改善行星齿轮传动系统的动力学特性,实现减振降噪、减小故障发生率具有重要的理论价值和工程意义。
国内外专家学者对其进行了诸多有益研究。Kahraman 等[1-2]建立了具有齿侧间隙的直齿圆柱齿轮副非线性动力学模型,运用谐波平衡法来研究内外激励作用下系统的振动情况;Han等[3]计入时变啮合刚度与轴弯曲等因素,建立了具有多自由度的单级齿轮系统,并对其振动响应特性进行了较为详细的研究;郇立荣等[4]建立了变载荷激励下故障半直驱风电行星齿轮传动系统动力学模型,引入了随机风载及故障动态参数激励,分析了系统的动态响应和时变载荷激励下含故障的行星齿轮系统的动力学特性;叶福民等[5]利用Kato公式法,分析了内激励对齿轮副振动噪声的影响;许华超[6]等基于齿轮系统动力学推导出行星齿轮传动系统的平移-扭转耦合非线性振动微分方程,采用特征值问题解法求解其固有频率及振型,并进行归类和描述;秦大同等[7]采用Runge-Kutta 数值积分方法求解了变载荷激励下半直驱风电行星齿轮系统的动态响应,并分析了激励对系统动态特性的影响规律;陈裴等[8]采用多体动力学方法对某船用行星齿轮进行刚柔耦合仿真,将发生故障后的动力学响应与正常状态进行对比。
由于风机齿轮箱结构的不规则性,在进行行星齿轮系统的动力学特性分析时以上研究未对包括箱体在内的整机振动进行研究。目前缺少对功率分流式两级行星齿轮和箱体的整机多体动力学特性的研究。
本文以某风电功率分流式6 MW风机增速箱为研究对象,基于多体动力学的刚柔耦合模型对其整机动态特性进行研究,为增速箱的动态设计和优化提供依据,以提高动态特性下的强度和寿命。
1 基于刚柔耦合多体动力学模型增速箱总成模态与谐响应分析
1.1 基于Romax 增速箱总成刚柔耦合多体动力学模型建模
增速箱的功率分流是通过将输入功率分别输入一级行星轮保持架和二级行星齿轮圈,以此明显降低低速端的扭矩负载,降低其应力。
增速箱功率分流拓扑图如图1所示。
功率先分给一级行星轮和二级齿圈,最后通过一级行星轮汇集到太阳轮轴,输出到连接发电机的平行轴系。
面向生产的三维模型有众多的倒角、圆角、螺栓孔和油管及油孔,这些特征对模拟计算结果影响不大,但是给有限元的网格划分带来诸多不便,所以首先对6 MW 风机增速箱几何模型进行必要的简化。部分组件的简化如下图2所示。

图1 增速箱功率分流拓扑图

图2 前箱体盖的简化模型
增速箱多体耦合模型中齿轮轮齿和轴承简化为弹簧阻尼单元;而行星轮轴和太阳轮轴及三级输出轴按集中参数模型简化;对其他箱体等结构建立其有限元模型,考虑其弹性变形。

图3 三级输出轴
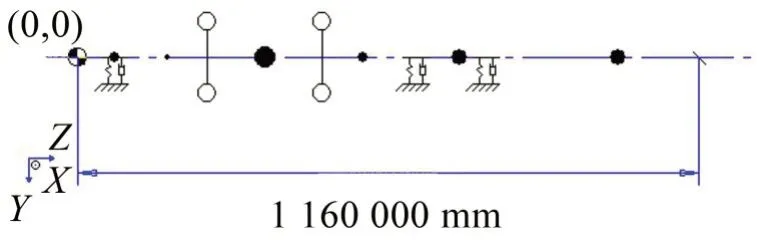
图4 三级输出轴集中参数模型
其中各箱体部分之间的螺栓安装用接触面部位的节点耦合进行模拟,如图5所示。

图5 前后箱体有限元节点耦合模型
增速箱后箱体两端吊耳通过液力耦矩器与风机基体相连,模型中以弹性连接的方式利用限位力元进行扭转和周向位移约束。增速箱总成耦合模型如图6所示。
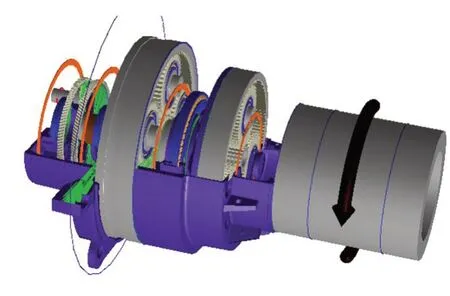
图6 增速箱总成耦合模型
部件材料属性如表1所示。

表1 材料属性
增速箱输入端受到来自风机叶轮的轴向扭矩,其额定工况载荷如表2所示。

表2 额定载荷
1.2 增速箱模态分析
考虑增速箱输入端转速较低而输出端转速较高的特点,在对增速箱主要部件进行模态分析时,主要分析增速箱中速度较高的三级输出齿轮轴系和三级输入齿轮轴系,此外,一级太阳轮轴属于细长轴,且相对转速较高,因此也有必要对其进行模态分析。
1.2.1 模态分析频率范围
根据额定转速确定的模态分析频率范围如表3所示,转速的上下限分别取额定转速的30%。

表3 频率分析范围/(r∙min-1)
前箱体主要激励频率为一级行星齿轮的啮合频率和二级行星齿轮系内齿圈的啮合频率,如表4所示。
对增速箱各部件进行模态分析时,主要考虑各部件在所受激励频率范围内的各阶固有频率,由于两级行星轮系均为平行齿轮,而三级人字形斜齿轮的啮合轴向力内部平衡,此外,两级行星轮太阳轮和内齿圈的齿轮啮合激励沿周向均匀分布且啮合激励均处于轴系末端,因此,对增速箱进行模态分析时,主要考虑两级行星轮系的扭转振动、后箱体横向振动和三级输出轴的扭转及弯曲振动。

表4 行星轮系频率分析范围/(r∙min-1)
1.2.2 主要模态振型与频率
对增速箱前箱体、二级太阳轮轴、一级太阳轮轴、三级输入轴、三级输出轴和后箱体进行部件非耦合模态分析,在工作转速对应的各齿轮啮合频率内均不存在固有频率或扭转固有频率,增速箱总成在工作转速范围内的扭转模态均是由各部件之间的耦合作用形成的。

图7 总成68.5 Hz对应的耦合模态振型
对处于工作转速范围内的耦合振型进行分析,前箱体+二级太阳轮轴+一级内齿圈+一级太阳轮轴在68.5 Hz 处存在耦合固有频率,振型为扭转振动,且固有频率处于一级行星轮工作转速对应的啮合频率范围内。

图8 总成102.8 Hz对应的耦合模态振型
一级内齿圈保持架+一级内齿圈+二级太阳轮在102.8 Hz 处存在耦合固有频率,振型为1 阶扭转振动,固有频率同样处于一级行星轮工作转速对应的啮合频率范围内。
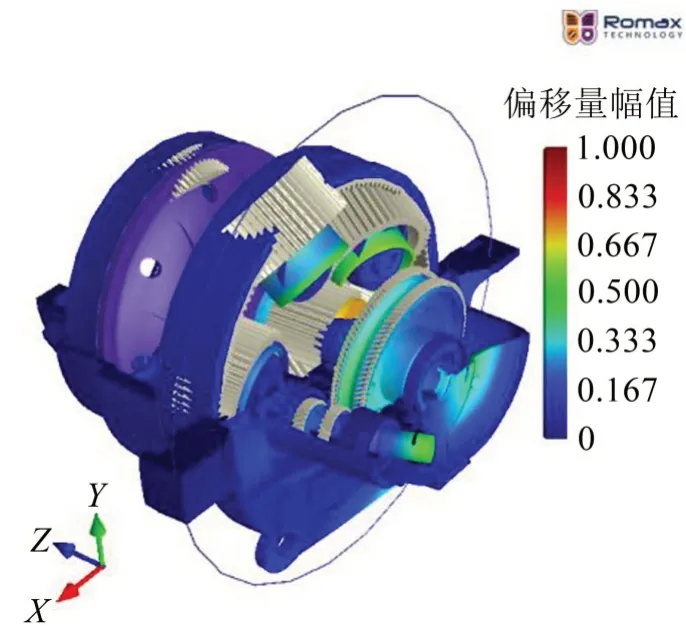
图9 总成346 Hz对应的耦合模态振型
箱体后盖+三级输出齿轮+二级太阳轮在346 Hz处存在耦合固有频率,振型为齿轮的摆振和后盖的横向振动。
1.3 增速箱谐响应分析
为了进一步分析各级齿轮啮合激励对增速箱不同模态振动的贡献度,对增速箱在不同齿轮啮合激励下的谐响应进行分析。
分别在前箱体、保持架和后箱体选取对应节点作为谐响应输出点,如图10、图11所示。

图10 保持架和前箱体响应点分布

图11 后箱体响应点分布
图12至图14分别为一级内行星轮啮合激励和二级内行星轮啮合激励及三级齿轮啮合激励下各节点谐响应振动位移频谱图。

图13 一级行星轮系啮合激励下节点2振动位移频谱图

图14 三级平行轴啮合激励节点3振动位移频谱图
由图2至图14可知,在69 Hz和105 Hz、344 Hz、490 Hz附近存在振动位移的峰值。
如表6所示为增速箱各部件节点在各啮合激励下的主要共振振幅及对应激振频率。

表5 工作转速内各阶固有频率和振型

表6 共振转速下各节点共振响应幅值和共振频率
2 基于刚柔耦合多体动力学模型增速箱总成稳态响应分析
2.1 基于Simpack的增速箱总成刚柔耦合多体动力学模型建模
对增速箱部分结构进行子结构柔性化处理,同时为了缩小计算规模,利用子结构分析方法对柔性部件的模态向主节点进行缩减,获得子结构部件的刚度和质量缩减矩阵,对柔性部件进行模态筛选,确定柔性部件特征模态矩阵。增速箱模型中将高速轴、一级太阳轮轴、箱体轴承支座、一级端盖-二级太阳轮轴系等轴径尺寸比较大或内部关键部件进行柔性化处理。对将齿轮箱箱体和轴向尺寸较小的行星轮轴和人字齿轮、行星轮设为刚体部件。图15所示为关键柔性体部件和刚体部件。

图15 柔性高速轴和刚性平行轴大齿轮
增速箱各部件之间的装配关系通过joint中的不同装配关系模型实现,增速箱各齿轮、花键和轴承分别通过齿轮力元、花键力元、限位力元和轴承力元等力元模型进行模拟。

图16 增速箱多体动力学模型
模型以x方向为轴线方向,z方向为水平方向,y方向为竖直方向。
增速箱受到来自外部风载导致的变载荷和内部齿轮啮合导致的变刚度激励影响。在不考虑外部风载变化的情况下,对增速箱总成在内部齿轮啮合产生的内部啮合激励下的振动响应进行分析。
2.2 增速箱稳态响应分析
在额定工况下对增速箱进行稳态分析,获得各轴系关键点的振动幅值如表7所示。振动主要出现在一、二级行星轮系,其中一级行星轮系的振动较大。

表7 各轴系振动指标/mm
一级太阳轮径向振动位移曲线如图17所示。

图17 一级太阳轮y方向振动位移
一级行星轮系齿轮啮合刚度突变较多,说明存在较为明显的冲击载荷,二级行星轮系齿轮啮合刚度较为规整,突变较少,齿轮啮合冲击激励较少。
为了分析增速箱啮合激励的频率成分,对增速箱一级太阳轮轴、二级太阳轮轴和高速轴的内部啮合激励进行频域分析。表8给出额定工况下各轴系啮合力中不同频率成分的幅值。

表8 额定工况下各级啮合激励频率成分及对应幅值
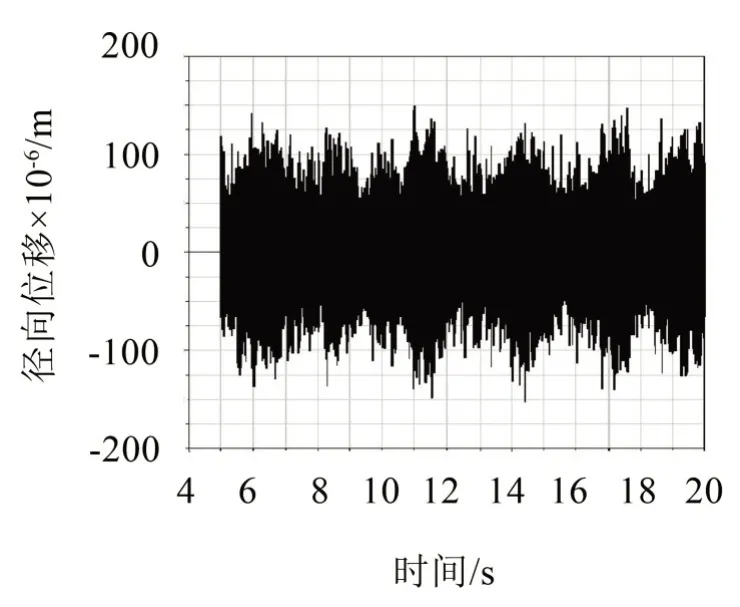
图18 二级太阳轮y方向振动位移
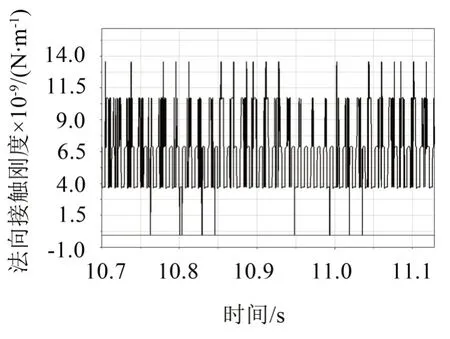
图19 一级太阳轮-行星轮1啮合刚度

图20 二级太阳轮-行星轮1啮合刚度
由表8可知,在额定工况下80 Hz的啮合激励频率和振动频率分布在增速箱各轴系的啮合激励频率成分中,是造成增速箱振动的主要原因。
3 结语
(1)工作转速范围内,增速箱存在68 Hz 和102 Hz对应的扭转振型及346 Hz对应的耦合摆振振型,其中68 Hz对应的前箱体的扭振会导致一级内齿圈保持架+一级内齿圈和一级太阳轮轴的扭转振动,而102 Hz 处以一级内齿圈保持架+一级内齿圈扭转振动为主,导致一级太阳轮随其扭转振动。
(2)通过对增速箱模态和谐响应分析可知,激起增速箱共振响应的内部激励主要是一级行星轮啮合频率和三级人字形齿轮的啮合频率。
(3)在额定工况下,增速箱一级内齿圈的振动造成其啮合激励中出现较多的冲击载荷,其中80 Hz的激励频率及其倍频是造成增速箱振动较大的主要原因。
