考虑车桥接触非线性因素的桥梁动力响应研究

周子骥，高芳清

(1.西南交通大学 力学与工程学院，成都610031；2.西南交通大学 应用力学与结构安全四川省重点实验室，成都610031）

随着现代交通事业的迅猛发展，公路车辆的运行速度及荷载均有大幅度提高，车辆对桥梁结构的动力作用显著增加[1-2]。对于行驶中的车辆而言，地面对车辆的影响显然比空气影响更为显著。地面作用力通过轮胎传递至汽车，因此作为车桥接触构件的轮胎是车桥耦合研究的重要部分。车辆行驶过程中，尤其是发生跳车情况，轮胎与桥面接触的过程往往存在大变形。因此由轮胎大变形引起的车桥接触非线性效应该予以关注。

XW Liu 等[3]运用半解析法研究车轮瞬时跳跃时的车桥动力相互作用问题。刘钰等[4]建立车辆过桥时由于桥面不平度引起的跳车情况下的车桥耦合振动计算模型，通过数值模拟来研究跳车情况下桥梁的动力响应。周子骥等[5]建立1/4 车辆模型研究了桥面障碍物引起跳车情况下的桥梁动力响应。虽然更深入研究了桥梁动力响应问题，但是上述研究均将车桥接触看作是线弹性接触而未涉及接触非线性问题。1979年，Captain基于轮胎变形和受力之间关系，从理论上推导了轮胎刚度模型[6]。刘任先提出轮胎刚度的多项式回归模型[7]；其后管迪华根据轮胎的模态参数建立了便于离散计算的时域仿真模型[8]；最后陈栋华等通过振动试验台进行轮胎动静态试验，提出反映轮胎变形、轮胎压强和外激励频率等轮胎刚度的非线性解析模型[9]。此模型的提出为车桥接触非线性的研究奠定了基础。因此可以在前人对车桥接触构件所进行的研究基础上，结合桥梁动力响应问题研究方法，进一步研究考虑车桥接触非线性时的桥梁动力响应问题。

结合简支梁桥特点，采用简构车辆和简支梁桥模型，通过胎压非线性模拟、基于泰勒展开的车桥接触刚度拟合、车桥耦合非线性动力学方程的改进与建立、“新型预测-校正积分”数值求解方法的引用等工作，对不同跳车高度和车速情形下的桥梁动力学响应进行计算分析，并与基于车桥耦合作用线性方程的分析结果进行对照，探究车桥接触非线性与线性条件下分析结果的差异。

1 车桥接触非线性的研究

1.1 轮胎模型的建立

车辆轮胎是汽车的重要部件，是将车辆荷载传递给桥梁结构的主要构件，是车桥接触的枢纽。在车桥耦合研究中，尤其是在特殊行车状态时的桥梁动力学研究中，轮胎往往存在大变形，因此轮胎与桥梁的接触非线性效应尤为明显，所以需要在轮胎冲击桥梁时刻进行仿真研究。

在建立系统模型过程中需进行合理的简化。由于主要研究胎压变化与轮胎非线性关系，所以桥梁简化为刚性路面。在轮胎橡胶区域使用实体solid185 单元，对内部气体使用solid242 单元，用质量单元mass21 模拟轮胎连接结构件的质量，用conta173 和targe170 接触单元模拟轮胎与地面的接触，用conta175 和targe170 接触单元模拟轮毂的支撑作用，用solid265 单元模拟钢丝加固层。设定轮胎区域边上网格数量，可使截面网格形状较为规则，然后沿轮胎轴向方向扫略生成整个轮胎网格。轮胎与桥梁有限元模型如图1所示。

1.2 轮胎压强变化公式

轮胎非线性因素主要与胎压有关。轮胎压强变化直接引起轮胎非线性效应的改变。在跳车冲击过程中，车辆下落冲击桥面时，轮胎压强变化尤为明显。因此，研究车辆冲击桥面时的轮胎压强变化对研究轮胎非线性效应尤其重要。

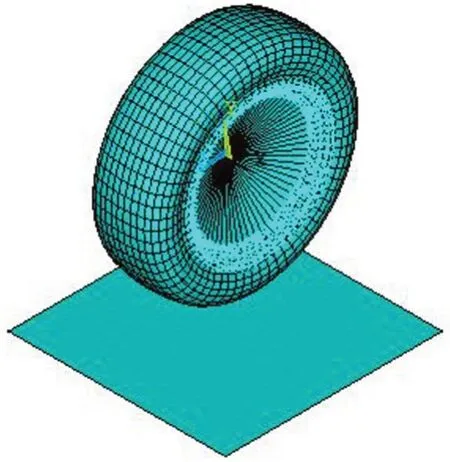
图1 轮胎与桥梁有限元模型

对于重车，根据规范《GB/T2977-2016 载重汽车轮胎规格、尺寸、气压》，选取参数为10.00R20 轮胎进行研究。轮胎充气后胎压为830 kPa，承受荷载为1/6车辆重量，下落高度为50 mm。

轮胎在车辆重力荷载作用下开始自由下落，冲击桥面。其求解运算分为4个步骤：

(1）施加初始温度和车辆荷载；

(2）施加充气压强；

(3）删除压力和位移约束；

(4）自由下落撞击桥面。

计算后得到如图2所示的轮胎压强变化曲线：

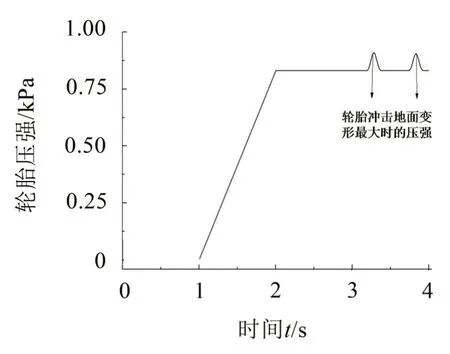
图2 轮胎压强变化过程图

由压强变化曲线可知，轮胎在前1 s时初始温度为27°C。从1 s开始压强增大使得轮胎初始压强达到830 kPa。从3 s 开始轮胎受车辆重力作用而下落，在3.177 8 s 时接触桥面。轮胎下落时最大压强为909 kPa，压强最大时间出现在3.276 s。在3.411 4 s时，轮胎压强恢复。根据ANSYS模拟结果可知，轮胎压强变化与时间成线性关系；轮胎从下落撞击桥面开始变形到变形恢复所用的时间与轮胎下落高度有关。拟合ANSYS数据曲线，可以得到胎压与下落高度关系，即

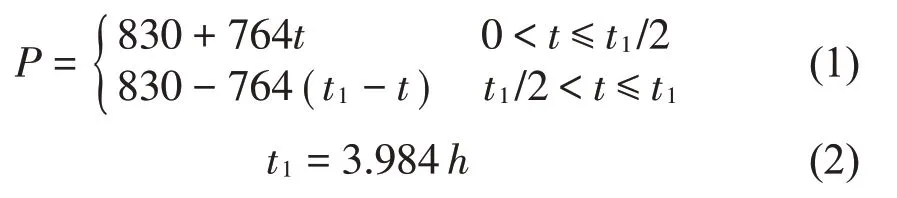
其中：P为压强，单位是kPa；t1代表从轮胎下落撞击桥面开始变形到变形恢复所用的时间，单位是s；h代表下落高度，单位是m。

1.3 轮胎刚度与压强关系

由文献[9]可知，轮胎的受力与其刚度有关，即

其中：F代表受力大小，单位为N；δ代表轮胎变形量，单位是mm；k1、k2为刚度系数，单位分别为N⋅mm-1和N ⋅mm-2。

同样由文献[9]可以得到kl和k2值与胎压变化P关系的准确表达式。即

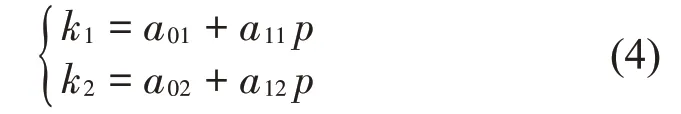
其中：kl、k2为轮胎刚度的相关量，单位分别为N ⋅mm-1和N ⋅mm-2；P为胎压，单位为kPa；a01、a11、a02、a12为系数，单位分别是N ⋅mm-1、mm、N ⋅mm-2、mm；其中a01、a11、a02、a12数 值 分 别18.204 0 N ⋅mm-1、0.626 2×10-6mm 、-0.675 4 N ⋅mm-2、0.010 5×10-6。

2 非线性方程建立与求解

桥系统的计算模型见图3。

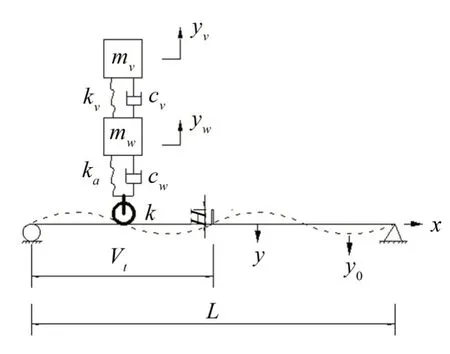
图3 考虑轮胎非线性时的车桥耦合模型

其中：yw、yv与y分别表示汽车悬挂结构、车体和桥的位移；y0表示路面不平顺；mw、mv分别为汽车悬挂结构和车体的质量；cw、cv分别是汽车悬挂结构和车体的阻尼；k、ka、kv分别是汽车轮胎、汽车悬挂结构和车体的刚度。桥梁长度为L，单位长度质量为m，抗弯刚度为EI。H为障碍物高度。K与k1、k2有关，kw代表轮胎和悬挂结构非线性刚度。

2.1 轮胎与悬挂结构刚度拟合

由式（3）可知轮胎刚度k=k1+k2δ。由图3可知，轮胎刚度和悬挂结构刚度组成串联系统，因此其串联刚度为

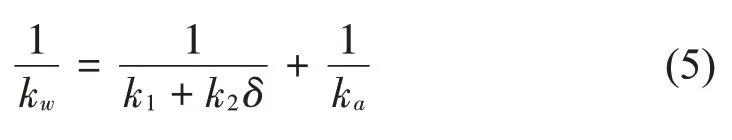
其中：kw为悬挂结构和轮胎整体刚度，δ为轮胎变形量。将式（5）化简可得

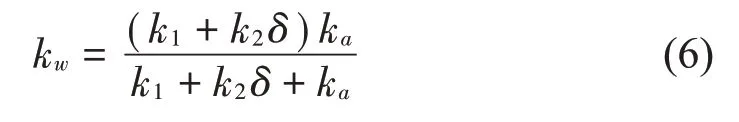
虽然k2的数值大小远远小于k1和ka，是其值的1/60，但是轮胎变形量δ较大，因此分母中k2δ不能省略。运用泰勒展开式可将整体刚度表示为

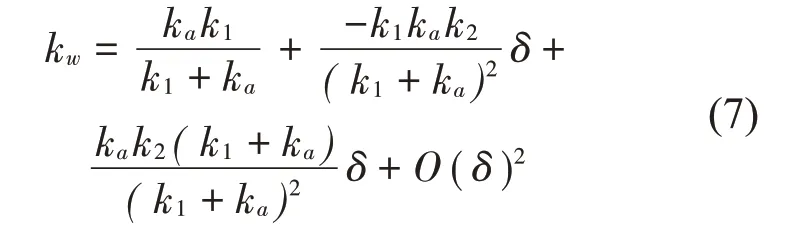
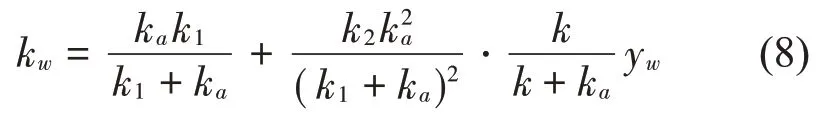
2.2 车辆与桥面接触

车辆轮胎与桥面保持接触时，车-桥系统方程为耦合方程，即

将方程式（11）按照模态展开并积分，由φi(x)正交性，可以得到

令mv+mw=mt，将上述公式代入式（9）、式（10）、式（13）中得到

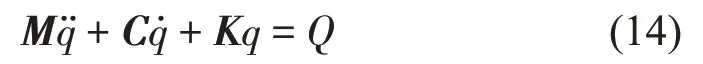
其中：M、C和K分别为(i+2)阶质量、阻尼和刚度矩阵，Q为(i+2)阶荷载向量，q为(i+2)阶向量。表达式如下

2.3 车辆离开桥面过程

跳车即车辆轮胎受到障碍物影响而腾起，与桥面发生脱离，对应时间为ts≤t＜ts+tL。tL表示车辆离开桥面腾空时间。车-桥系统可用非耦合方程表示为

写成矩阵形式

其中矩阵M2、C2、K2和向量Q2、q分别为

对于跳车持续时间tL：y+y0+yw+H-0.5g⋅tL2≥0。

3 算法选取与路面不平顺

3.1 算法选取

文中计算涉及非线性方程组，使用Newmark 隐式法计算，虽然稳定性较好，但是由于每步积分都需要求解高阶线性代数方程组，且需要重新计算刚度矩阵，其时效性较差；使用Newmark显式法计算，虽然稳定性较好，但是显著受稳定性限制，容易影响计算精度。为保证结果精确性与时效性，互补2 种计算方法的优缺点，采用翟婉明提出的“新型预测-校正积分”方法来进行数值求解[10]。

预测式修正

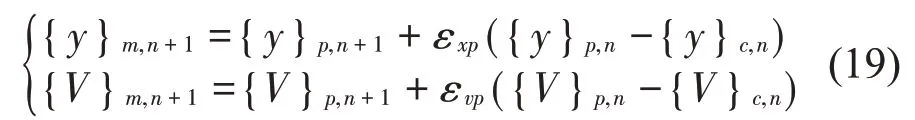
校正式修正

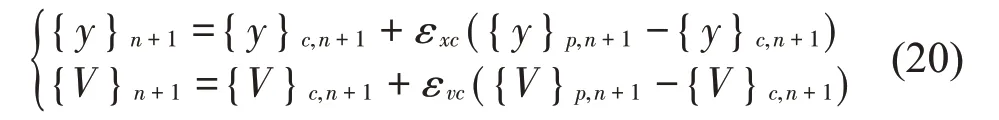
由此构成的预测与校正积分模式，共分为6 个步骤：

（1）进行预测{y}p,n+1，{V}p,n+1；

（2）校正，求得{y}m,n+1，{V}m,n+1；

（3）通过计算，求得{A}p,n+1={M}-1({P}n+1-(K)n+1{X}n+1- {C}n+1{V}p,n+1)；

（4）校正{X}c,n+1、{V}c,n+1；

（5）改进{X}n+1、{V}n+1；

（6）计算{A}n+1。

初始条件为

得到

于是便可以开始积分了。

其中ε为误差补偿系数，下标p、c、m代表预测值(predict)、校正值(correct)、改进值(modifier)；下标n和（n+1）表示t=nΔt 和t=(n+1)Δt 的响应量；{C}n+1、(K)n+1表示(n+1)Δt时的瞬时阻尼、刚度矩阵，仅对线性问题才为定值。{M}为质量阵，{A}(或{y})、{V}为广义位移、速度矢量。

3.2 路面不平顺

国内外学者对路面进行大量测试和研究，通过傅里叶变换将路面功率谱转化为表面平顺度数据。其桥面平顺度数据可以描述为

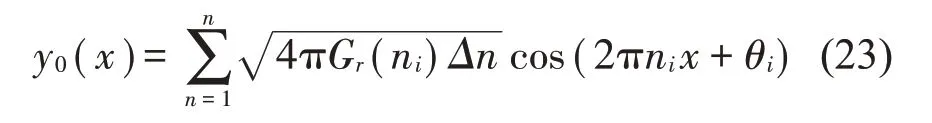
式中：θi为[0,2π]上均匀分布的随机数；ni是空间频率，Gr(ni)为路面功率谱函数。

图4为利用傅立叶逆变换法得出的路面较差的A、D级路面随机不平顺样本。

4 算例与分析

桥的参数为：EI=2.05×1010N ⋅m2，m=9.36×103kg/m，L=24 m。车辆的参数：mv=15 670 kg，mw=2 530 kg，Cv=10 000 N ⋅s/m，Cw=5 000 N ⋅s/m，kv=1.8×106N/m ，P=830 kPa，ka=126×106N/m。结构阻尼参数η=0.001；时间步长Δt=0.001 s。

4.1 起跳高度不同时的跳车冲击过程计算结果比较

桥面不平顺取A、D级路面不平度，车辆速度取V=10 m/s。考虑车辆起跳高度H=0.03 m、0.05 m时，冲击点选择为跨中。比较在不同起跳高度情况下，考虑车桥接触线性与非线性时跳车冲击对桥面竖向动态位移响应的影响差异。计算结果如图5所示。

车辆过桥过程计算结果表明：当跳车高度H=0.05 m 时，车桥接触线性与非线性两种情况对桥梁跨中竖向位移值影响尤为明显，最大差异超过4 mm；考虑接触非线性时，桥梁跨中竖向位移值有所增加。车辆未处于跳车状态时，考虑接触非线性对桥梁位移值的影响与其线性情况影响差异很小。路面不平顺度越高，接触非线性和线性差异越明显。

4.2 车辆速度不同时的跳车冲击过程计算结果比较

桥面不平顺取A、D级路面不平度，障碍物高度H=0.03 m，车辆速度V=10、20 m/s 时，考虑在桥梁跨中处发生跳车冲击现象。比较不同车速情况下，考虑车桥接触线性与非线性时跳车冲击对桥面竖向动态位移响应的影响。

桥梁跨中响应如图6所示，计算结果表明：车桥接触非线性对桥梁竖向位移响应的影响与速度有关；当V=10 m/s时，接触非线性与线性条件下桥梁跨中位移值相差超过2 mm，当V=20 m/s 时，其差异超过1 mm；随着速度增大，接触非线性影响减弱。车辆行驶速度越快，路面不平度使接触非线性对桥梁影响越减弱。

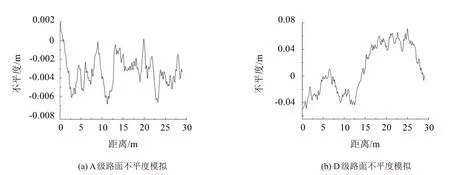
图4 桥面不平度模拟

图5 跳车高度不同时轮胎线性与非线性差异

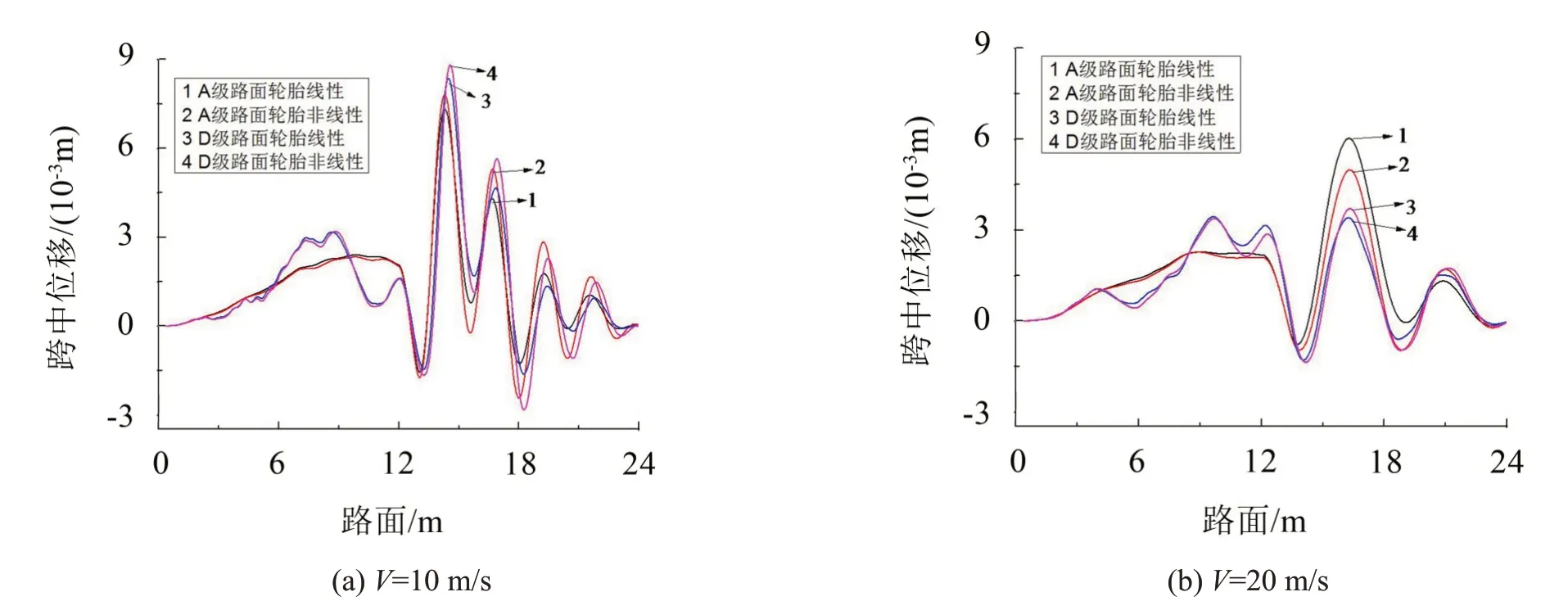
图6 车速不同时轮胎线性与非线性差异

5 结语

车辆过桥面发生跳车冲击过程时，考虑不同跳车高度、不同车速工况下，车辆对桥梁冲击作用受轮胎非线性影响程度。

(1)考虑车桥接触非线性与轮胎线性两种情况，车桥接触非线性会使桥梁跨中竖向位移值增大。

(2)车辆未处于跳车状态时，车桥接触非线性与线性两种情况对桥梁竖向位移值影响差异不明显。而出现跳车状况时，车桥接触非线性对桥梁竖向位移值的影响与轮胎线性条件下相比，差异明显。因此研究发生跳车冲击时的桥梁动力响应，应该考虑车桥接触非线性效应影响。

(3)桥面不平顺度越高，车桥接触非线性对桥梁竖向位移值影响越明显，但是其影响趋势不太显著。

因此，当不考虑车辆跳车冲击时在桥面耦合行驶时，可以忽略车桥接触非线性的影响；而当考虑特殊行车状态时，应该考虑车桥接触非线性影响。