小型大幅值两轴振动台优化设计

高玉龙，张 啸，杨斌堂

（上海交通大学 机械系统与振动国家重点实验室，上海200240）

振动试验是机电产品抗振性能和可靠性检定的必备手段，在航天、航空、兵器、船舶、核工业等国防工业领域以及汽车、建筑等民用工业部分都有广泛的应用[1]。

而振动台是实现振动模拟实验的物理基础和实现载体，可适用于不同规格试件的振动环境试验[2-3]。传统的振动试验采用的是单轴振动试验方法，实验设备是传统的单轴电动式、电液式振动台或单轴振动台加水平台，它对现代工业的发展做出了巨大贡献，但单轴运动模拟实际振动环境的真实性存在很多问题，实验结果背离实际，常出现欠试验和过实验的情况[4]。随着多点激励振动控制方法的研究，采用多个单轴振动台在多个方向上进行多自由度振动模拟实验越来越普遍，其中使用较多的是两轴或三轴振动台[5]。另外，随着并联机构的研究深入，其高刚度、高负载能力、高动态性能等优点越来越受到多轴振动台研究者的重视，并成功开发出了基于并联机构的多自由度振动台，大大提高了振动试验技术[6-7]。

当振动台作为综合性能测试仪中一个测试模块时，往往要求其具有紧凑性、模块化、小型化等特点。虽然目前市场上的小型振动台种类和品牌多样，但都很难实现大幅值激振，比如东菱ES-3-150 型振动台[8]、埃特斯力ITS03 型振动台[9]以及亿恒EDS-300型振动台[10]等。它们具有相同的推力、加速度和频带指标，但激振幅值都只有12.5 mm。因此，文中将在此类振动台的基础上，开发具有更大幅值且较宽频带的小型两轴振动台，以适应研制综合性能测试仪测试模块的需求。

1 小型两轴振动台方案介绍

小型两轴振动台采用两个单轴振动台分别在x、y方向激振进行振动模拟实验。由于电动振动台频带宽，加速度大，易于实现随机控制，可以实现大位移、大推力[11-12]，故本文选用杭州亿恒科技有限公司的EDS-300 型电动振动台，在其基础上扩大其激振幅值，保证其较高的工作频带。EDS-300 型电动振动台部分性能指标如表1所示。

表1 EDS-300型电动振动台部分指标

由表1可知，该电动振动台尺寸小，输出位移振幅仅有12.5 mm，故考虑对电动振动台的激振幅值进行放大。低频时为尽量提高激振幅值，采用幅值放大，但在高频激振时，为保证激振频率和加速度，不采用幅值放大。具体的两轴振动台方案设计如图1所示。

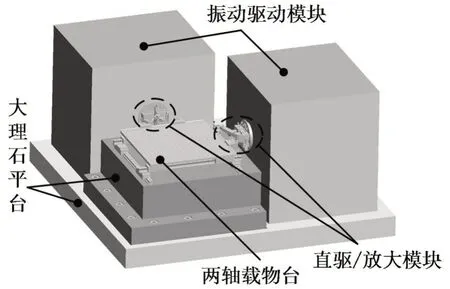
图1 两轴振动台总体方案

两轴振动台的基台选用大理石平台，对来自地面3 Hz 以下的振动进行隔振；两台EDS-300 型电动振动台安装在大理石平台上，由一个振动控制仪控制其工作，可同时分别从x、y两垂直方向进行激振；振动信号通过直驱/放大模块传递到两轴载物平台上；两轴载物平台由高性能滚柱直线导轨和滑块搭建而成，提供x、y方向两轴运动，能够承受较大的载荷；试件安装在载物平台上进行振动环境模拟实验。整个两轴振动台尺寸为1.6 m×1.6 m×1 m。

直驱/放大模块的具体结构如图2所示，激振信号通过剪叉结构进行放大。

图2 直驱/放大模块方案

剪叉结构主要由两根连杆组成，连杆传递激振力。对称布置的连杆在放大振幅的同时，消除了寄生位移。剪叉结构的销轴固定在大理石平台上，而其输入端和输出端通过轴承和支座固定，支座固定在滑块上。由于EDS-300 型振动台输出台面较小，故增加扩展台安装在电动振动台的台面上，以安装输入端直线导轨和支座等。

固定块的作用是进行直驱/放大模块的状态切换，具体原理如图3所示。

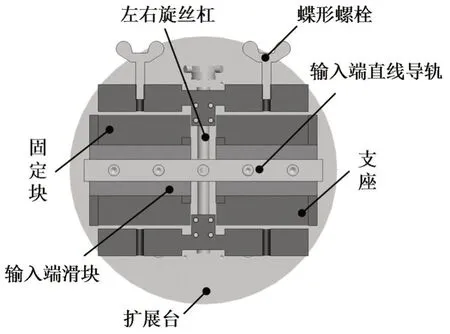
图3 直驱/放大状态切换方案

当需要高频激振时，旋转左右旋丝杠使固定块卡入输入端支座的槽中，并旋转蝶形螺母抵在直线导轨上，防止固定块在丝杠上松动，同时抽出销轴，切换至直驱状态。由于支座固定在滑块上，导致输入端和输出端的滑块都无法滑动，剪叉结构变成一个刚体，激振信号通过刚体剪叉结构直接作用在载物平台上。当需要进行低频大位移激振时，旋转左右旋丝杠，使固定块脱离支座的槽中，插入销轴，剪叉结构正常工作。

2 直驱/放大模块关键零件设计

2.1 连杆的设计

连杆的作用是传递电动振动台的激振信号，同时放大输出位移的幅值。因此需合理设计连杆的放大比，保证其结构强度，且其固有频率不在激振频率范围内。

如图4所示为连杆的部分重要尺寸。显然，连杆的长度越短，厚度和宽度尺寸越大，则其强度越高，固有频率也越大。

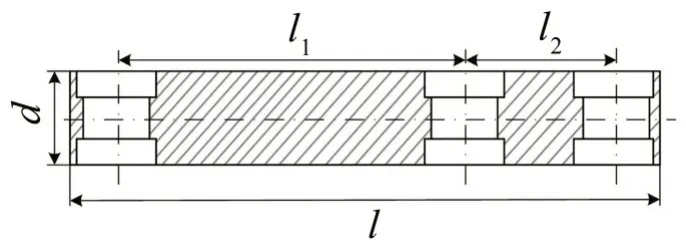
图4 连杆的重要参数尺寸

综合考虑振幅放大状态时各部件的运动情况、振幅指标和连杆的强度、固有频率等要求，取l1=105 mm，l2=45 mm，d=20 mm，连杆宽度b=30 mm，此时l=178 m。因此，振幅放大比为

此时两轴振动台的最大输出振幅和最大正弦激振力为

其中：A0为电动振动台的最大输出振幅，即12.5 mm；F0为电动振动台的最大正弦激振力，即2 940 N。

正弦推力公式为

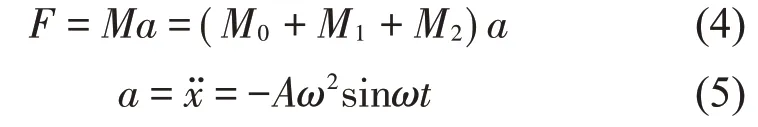
其中：M0为动圈质量，即为3 kg；M1为直驱/放大模块质量及两轴载物平台运动部件质量，取为2 kg；M2为试件质量；a为加速度；x为激振位移；A为激振幅值；ω为激振频率。

因此，根据推力公式可知，振幅放大状态时的振动台的空载加速度可达32 g。此外，代入最大正弦激振力和最大输出振幅，还可计算出，空载时输出最大振动位移时，最高工作区间可达5 Hz～93 Hz，实际工作时最大振动位移的低频区间需根据试件质量求出。

连杆承受的最大推力为2.94 kN，作用于连杆的两端孔上。如图5所示为连杆在最大推力作用下的有限元应力分析结果。连杆的最大应力为4.73 Mpa，显然满足结构强度要求。如图6所示为连杆的1 阶模态，其频率为4 906.6 Hz，远高于最大激振频率4 000 Hz。

图5 连杆在最大推力作用下的应力

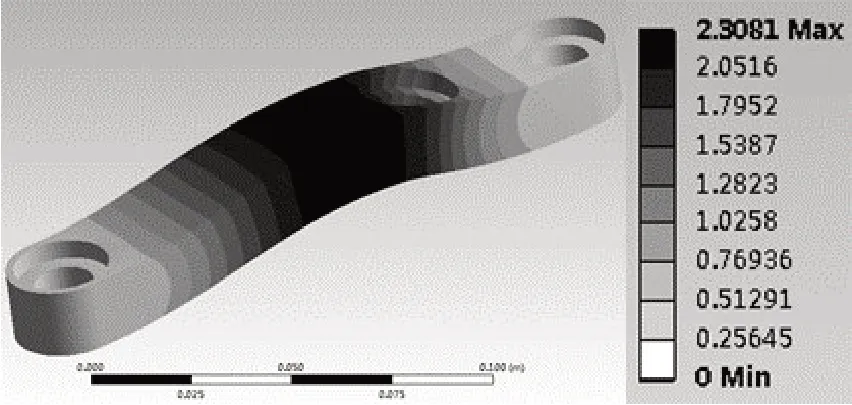
图6 连杆的1阶模态

2.2 支座的设计

直驱/放大模块中的支座关键尺寸为支座前端半径R和台阶高度t，如图7所示。支座前端半径越大，支座的固有频率越高。而台阶高度t影响连接刚度。

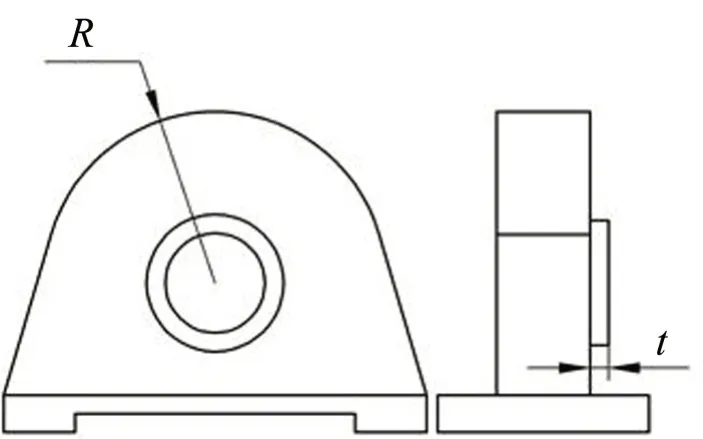
图7 支座的部分关键尺寸

初步设计时取支座前端半径为45 mm，台阶高度为3 mm，模态分析结果如图8所示。

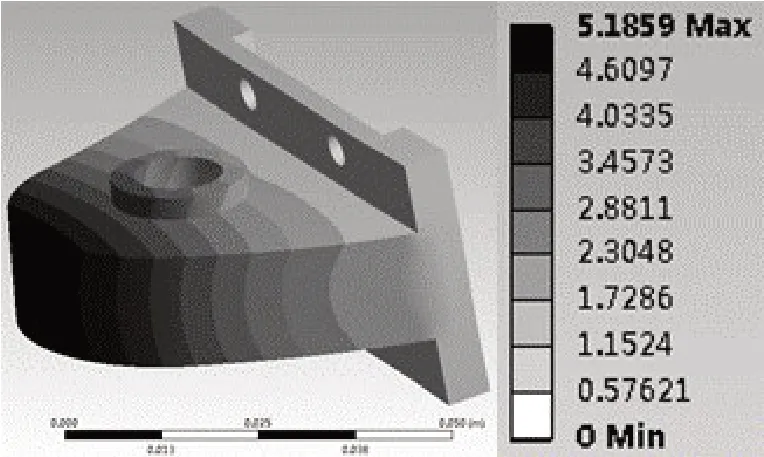
图8 输出端支座的1阶模态

其1阶模态为8 072 Hz，远高于电动振动台的最大激振频率。

2.3 固定块的设计

固定块用于直驱/放大模块在进行直驱时，卡入输入端的支座槽中，使直驱/放大模块的剪叉结构锁死，成为刚体，直接将激振信号传递到两轴载物平台上。因此，要求固定块在最大激振力2 940 N作用下具有足够的强度，且其1阶模态固有频率在3 000 Hz以上。

固定块设计为一个长142 mm、宽18 mm、高18 mm的长方体，其在最大激振力下的应力分布如图9所示，最大应力为28.7 Mpa，满足强度要求。固定块的1阶模态如图10所示。

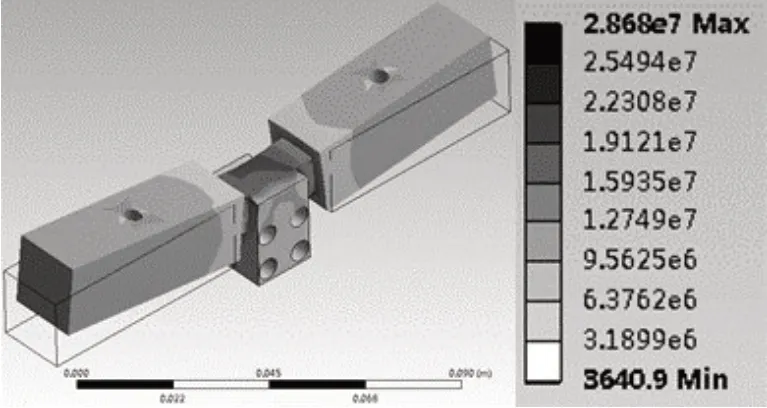
图9 固定块在最大激振力下的应力

图10 固定块的1阶模态

其1 阶固有频率为12 069 Hz，远高于最大激振频率4 000 Hz，因此固定块满足设计要求。

3 振动台1阶固有频率优化设计

3.1 模型简化与分析

虽然上述关键零件的设计保证了零件固有频率高于激振频率，但是两轴振动台整体的1 阶固有频率却还未知。因此，为保证足够宽的工作频带，需对其1阶固有频率进行分析优化。

首先对两轴振动台直驱状态下的模型进行简化。考虑两轴振动台的对称性，同时略去对振动台1阶模态无影响的部件，得到直驱状态下简化模型如图11所示。

简化后的直驱状态模型包含多个零件，相当于一个n自由度系统，其振动方程为

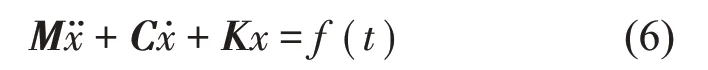
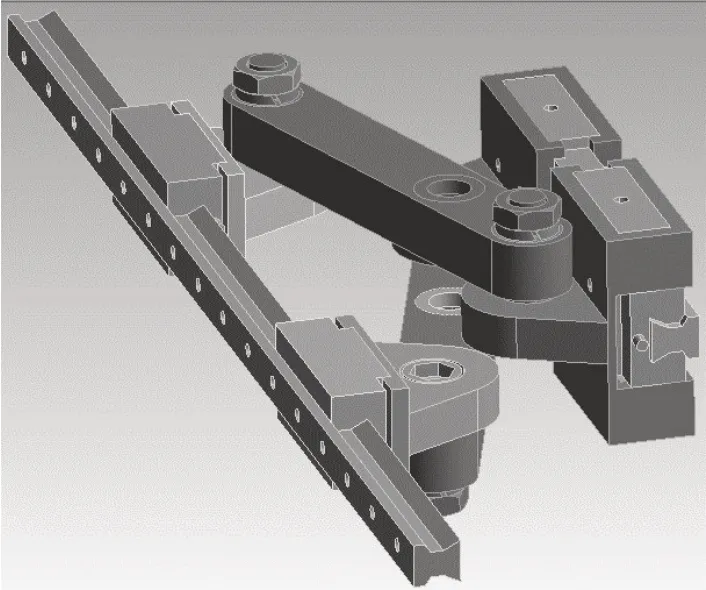
图11 简化后的直驱状态模型

式中：M为质量矩阵、C为阻尼矩阵、K为刚度矩阵为加速度列阵、为速度列阵以及f(t)为激振力列阵。

直驱状态下的材料阻尼以及轴承阻尼较小，影响可以忽略不计，则式(6)可变为无阻尼自由振动微分方程

式(7)中，当f(t)=0 时，系统为自由振动模式，通解为

式中：X是振幅列阵，将式(8)代入式(7)中，可得到振型方程

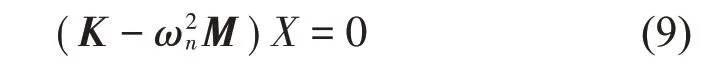
由式(8)和式(9)即可求出直驱状态下的模态频率和模态振型。对简化后直驱状态模型进行模态分析，得到其1阶模态如图12所示。

图12 直驱状态的1阶模态

固有频率为2 349.5 Hz，显然零部件之间的连接刚度不足，还需要对各零部件进行结构和参数优化。

3.2 零部件结构参数优化

为了优化直驱状态的1 阶固有频率，选取连杆的厚度d、宽度b以及支座的台阶高度t、前端半径R为优化参数，在保证直驱/放大模块运动不受干涉的前提下，以直驱状态的1阶固有频率为优化目标，进行有限元分析。

首先，针对连杆的厚度d进行优化，取厚度d=10 mm～25 mm，得到直驱状态的1阶固有频率随连杆厚度d的变化趋势如图13所示。

显然，连杆的厚度对直驱状态下的连接刚度具有一定影响，当d=17 mm，连接刚度最大，此时直驱状态的1阶固有频率为2 560 Hz。

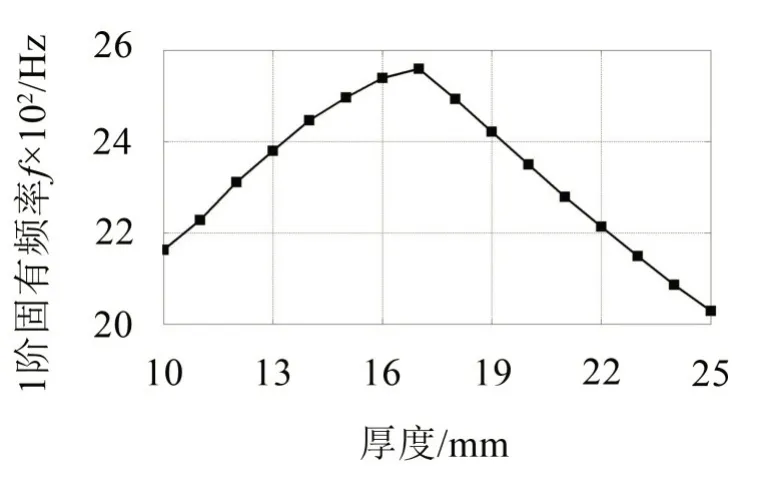
图13 直驱状态1阶固有频率与连杆厚度的关系

在厚度优化结果的基础上，针对连杆的宽度进行优化。由于连杆宽度过大则会和支座干涉，宽度过小则会影响轴承孔，故仅取宽度b=28 mm～36 mm，得到分析结果如图14所示。

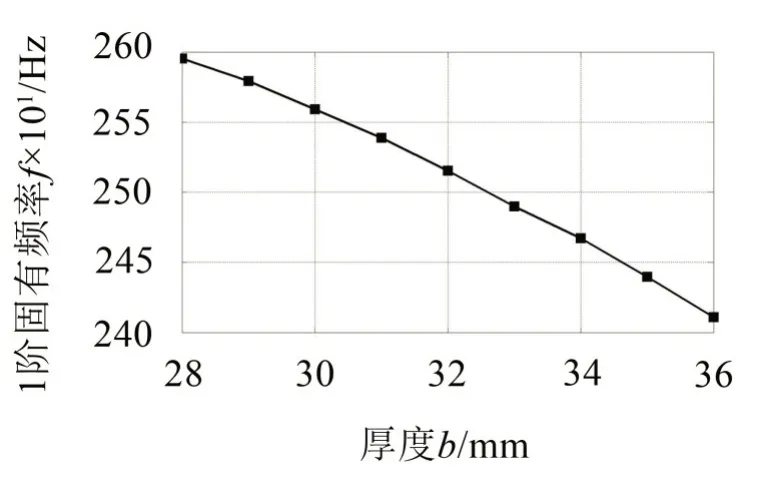
图14 直驱状态1阶固有频率与连杆宽度的关系

显然，在所选择参数范围内，连杆宽度越小，直驱状态1阶固有频率越高。因此，取d=28 mm，此时直驱状态1 阶固有频率为2 595.3 Hz。连杆的参数优化表明并不是零件的刚度越高，装配体的连接刚度也越高。

基于连杆的参数优化结果，针对支座的台阶高度t进行优化，得到直驱状态的1阶模态频率优化结果如图15所示。

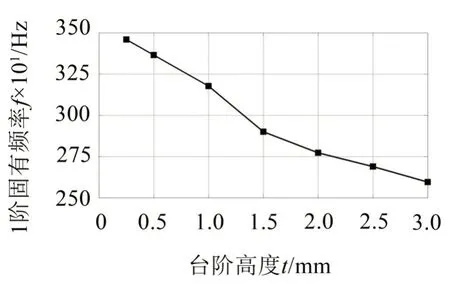
图15 直驱状态1阶固有频率与台阶高度t的关系

1 阶模态频率对台阶高度很敏感，台阶高度越小，相当于连杆和支座之间的间隙越小，连接刚度越大，1 阶模态频率越高。因此，取台阶高度为t=0.25 mm，尽量增大连接刚度，保证1 阶固有频率。此时直驱状态的1阶固有频率为3 458.7 Hz。

最后，基于上述优化结果针对支座的前端半径R进行优化，取前端半径R=25～65 mm，分析得到直驱状态的1阶模态频率优化结果如图16所示。

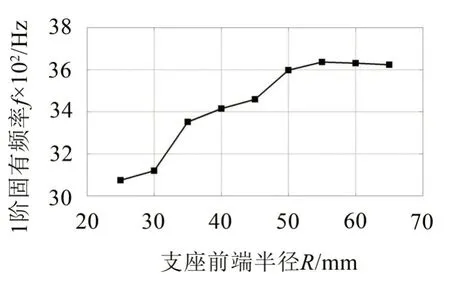
图16 直驱状态1阶固有频率与支座前端半径R关系

当支座前端半径开始增大时，直驱状态的1 阶固有频率随之增大，继续增大时，支座材料增加减少，故最终趋于平缓。根据优化结果，取支座半径R=55 mm，此时1阶频率为3 635.7 Hz。

在优化零件结构参数的同时，对支座的结构进行优化，比如增设加强筋、增厚支座等，以影响连接刚度获得直驱状态更高的1 阶固有频率。最终，经过零件参数的优化以及结构的优化之后，直驱状态的1阶固有频率为3 971.8 Hz，其模态如图17所示。

图17 直驱状态优化后的1阶模态

3.3 振动台工作频带

为了确定两轴振动台的工作频带，还需考虑直驱/放大模块在放大状态时的1阶固有频率。由于放大状态时剪叉结构是运动的，故分析剪叉结构在零位和两个极限位置时的模态和1阶固有频率。对放大状态时的两轴振动台模型进行简化，简化结果如图18所示。

图18 简化后的放大状态模型

图19 放大状态时不同位置的1阶模态

模态分析得到的结果是，放大状态在零位时的1阶模态频率为4 440.1 Hz，在位移最大处为4 369.4 Hz，在位移最小处为4 642.4 Hz，1 阶模态如图19所示。由此可以得出结论，两轴振动台能在5 Hz～3 971.8 Hz的频带内工作。

尽管两轴振动台无论是直驱状态还是放大状态都能在5 Hz～3 971.8 Hz 的频带内从低频到高频连续工作，但在低频时采用直驱状态达不到较大的输出振幅，而在高频时采用放大状态则达不到足够的激振力。因此，需要根据实验对象的振动环境模拟要求来决定切换至直驱状态还是放大状态。

4 结语

（1）本文在小型单轴电磁振动台的基础上，提出小型大幅值两轴振动台设计方案，解决了目前市场上小型振动台无法实现大幅值激振问题。

（2）采用剪叉结构放大输出振幅，放大比为2.33，最大输出振幅为29.17 mm。

（3）设计直驱/放大切换结构，低频下为获得大振幅，采用放大状态；高频下为获得较大激振力，采用直驱状态。

（4）通过结构优化设计，提高直驱状态的1阶固有频率，保证了两轴振动台可在5 Hz～3971.8 Hz频带内工作，但需根据试件的具体实验需求选择合理的直驱/放大状态。

（5）目前已经加工小型两轴振动台的实验样机，未来将通过实验验证两轴振动台的实际输出振幅和工作频带。