数列思想在生物学教学中的应用

王玉龙 马晋闽

(广东实验中学 广州 510055)

《普通高中生物学课程标准(2017年版)》明确指出以提高学生生物学学科核心素养为宗旨[1]。所以在课堂教学中，要注重对学生科学思维的培养。数列方法是构建数学模型的重要手段，也是培养科学思维的一种方式。在日常教学中，可以创设数学与生物学规律联系的桥梁，将学生所具备的数列知识充分挖掘与应用，引导学生通过数学建模解决生物学问题，深化对生物学规律的认识。

1 科学思维和模型建构

科学思维是观察和研究自然现象的思维范式，是具有意识的人脑对自然界中事物(包括对象、过程、现象、事实等)的本质属性、内在规律及其相互关系间接的、概括的和能动的反映[2]。模型建构是培养科学思维的重要方式和途径，生物学模型是借助某种手段对生命现象以及生命过程进行描述，用简洁的方式呈现生命规律。数学模型是一种重要的模型，是指用数学语言来表述实物的状态、关系和过程，是将生物学知识、实际问题与数学结合起来，以数学的形式反映生物学问题。在课堂教学中引导学生进行数学建模解决某些生物学问题，有利于培养学生的逻辑推理、计算、归纳、演绎等科学思维能力。

2 建构数学模型的实例

例： (2013年山东卷)用基因型为Aa的小麦分别进行连续自交、随机交配、连续自交并逐代淘汰隐性个体、随机交配并逐代淘汰隐性个体，根据各代Aa基因型频率绘制曲线如下图。下列分析错误的是

A. 曲线Ⅱ的F3中Aa基因型频率为0.4

B. 曲线Ⅲ的F2中Aa基因型频率为0.4

C. 曲线Ⅳ的Fn中纯合体的比例比上一代增加(1/2)n+1

D. 曲线Ⅰ和Ⅳ的各子代间A和a的基因频率始终相等

该题目具有较强的综合性，将自交、随机交配、全部个体都能存活和某一种特定基因型致死或淘汰等复杂情况结合在一起，并以数学曲线的形式来体现其变化规律，让学生加以判断，是高中遗传学上的一道比较复杂的习题。其中随机交配并淘汰隐性个体、自交并淘汰隐性个体的变化趋势是难点，常见的解题思路是： 算出杂合子在各种情况下F1、 F2、 F3中的比例，并依据图像作出判断。这种通过特例来判断曲线类型的方法用于解题十分简便，但并不利于学生对遗传规律本质的认识与理解。

在连续自交问题上，学生通常是用观察、归纳的方法看出规律，来理解杂合子比例的变化规律，即在逐代自交的过程中，杂合子以(1/2)n形式递减，虽然该结论是正确的，但由观察归纳所得出的结论是缺乏逻辑的必然性的，若将其转化为数学问题，将数学中的数列思想引入到该问题中，建立数学模型则可以顺利解决该问题。

2.1 连续自交，每代中杂合子比例变化规律 设Fn中杂合子Aa出现的概率为an，则Fn-1中杂合子Aa出现的概率可表示为an-1。

∵ Fn中杂合子Aa只能由Fn-1中杂合子Aa自交分离得到，且自交分离比为1/2

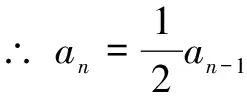
2.2 连续随机交配，每代中杂合子比例变化规律 随机交配的本质是亲本群体所能产生的雌雄配子，相互之间可随机结合。由于该情境下的亲本群体基因型均为Aa，故可产生各两种类型的雌雄配子A和a，且比例各占1/2。所以，雌雄配子之间的随机结合所产生的F1结果为AA、 Aa、 aa，比例分别为1/4、 1/2、 1/4。在计算由F1继续随机交配所产生F2时，可知所能产生的雌雄配子还是A和a，且比例依然为1/2，所以可得由F1至Fn，其中的杂合子比例均不再变化即为1/2。

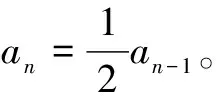
∵ Fn中的aa只能由Fn-1中杂合子Aa自交分离得到，且自交分离比为1/4

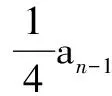
∵ 实际上Fn中淘汰了隐性个体aa

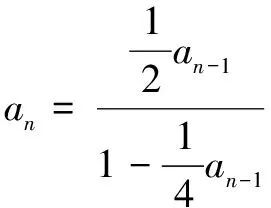
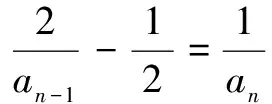
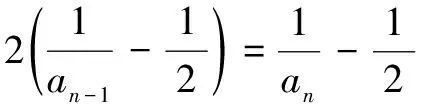
2.4 随机交配淘汰隐性个体，每代中杂合子比例变化规律 设Fn中杂合子Aa出现的概率为an，则Fn-1中杂合子Aa出现的概率可表示为an-1。

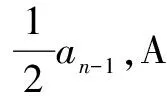
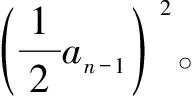
∵ Fn中的Aa为Fn-1所产生的配子A与配子a结合所得

∵ 实际上Fn中淘汰了隐性个体aa

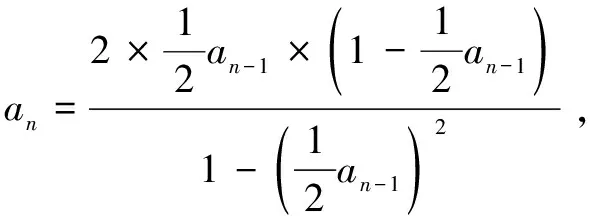
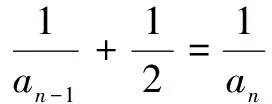
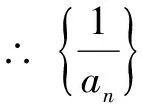
通过上述分析可以得出曲线Ⅰ为随机交配情况下的变化曲线，曲线Ⅱ为随机交配并逐代淘汰隐性个体的变化曲线，曲线Ⅲ为自交并逐代淘汰隐性个体的变化曲线，曲线Ⅳ为连续自交的变化曲线。可根据各曲线的变化规律对题目中的各个选项做出判断，进而选出该题的答案为C选项。

以上数学推导过程所用到的数学知识是高中生所普遍具备的，通过上述的情境转化，建立起生物学与数学间的桥梁，用数学知识解决生物学问题，让学生学以致用，用而致知。在此数学建模的过程也可让学生意识到： 高中生物学知识的学习不止局限于生物学教材中的内容；在现有的知识范围内，学生自己发现问题，加以深入思考后，可以解决某些问题，能够做知识的自我建构者，而非一味地被动接受知识；跨学科的数学建模是认识和解释某些生物学问题的有力工具；理科科目的学习是一体的，不同科目的知识和方法会相互渗透，而不应相互割裂开，在知识融合中深化对科学知识的认识。