Rn空间中几乎凸不等式系统的度量正则性与全局误差界

陈慧敏

( 西华师范大学数学与信息学院，四川南充 637009)

0 引言

在本文中, 考虑如下不等式系统：

f(x)≤0，x∈C，

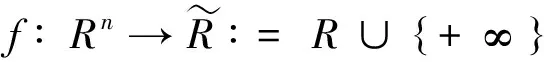
S∶={x∈C|f(x)≤0}=C∩(lev≤0f)，本文中始终假设集合S≠Ø.当X=Rn时,f为几乎凸函数, 集合C⊆Rn为几乎凸集，此时，称该系统为几乎凸不等式系统(1).当X=Rn时，f为凸函数，集合C⊆Rn为闭凸集，此时，称该系统为凸不等式系统(2).凸不等式系统(2)为几乎凸不等式系统(1)的特殊情况.

近年来，关于误差界、度量正则性和Slater条件的研究在数学规划中引起了广泛的关注.度量正则性已被认为是当代变分分析的核心概念之一，其在广义方程，变分不等式，优化等方面发挥着非常重要的作用(参见文献[1,2,3]).1998年，Deng[4]在Banach空间中证明了凸不等式系统的度量正则性、全局误差界和Slater条件之间的关系.在一定条件下，文献[5]在 空间中证明了几乎凸不等式系统(1)全局误差界的存在性，即：存在λ>0，使得

d(x,S)≤λ[f(x)]+，∀x∈C.

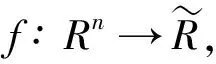
1 预备知识

首先回顾一些相关的概念与基本结论.

f(tx+(1-t)y)≤tf(x)+(1-t)f(y)，∀x,y∈S，∀t∈[0,1]，

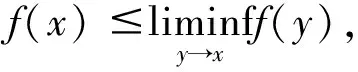
为证明主要结论, 我们需要如下定义、引理和命题.

定义1[6]设A，B是Rn的子集， 若clA=clB和riA=riB， 则称集合A和B近似相等， 表示为A≈B.

定义2[3]设A是Rn的子集， 若存在Rn的一个凸子集D， 使得D⊆A⊆clD， 称A为几乎凸集.

定义4[4]假设系统(1)的解集S非空且集合Ŝ⊂S， 若存在正常数δ和τ(δ)， 使得：

d(x,S)≤τ(δ)[f(x)]+当d(x,Ŝ)≤δ，∀x∈C

称系统(1)在集合Ŝ上有度量正则性，其中[f(x)]+=max{f(x),0}.

当Ŝ={z}时， 称系统(1)在z处有度量正则性.若系统(1)在z处有度量正则性，并且对任意的z∈S均成立， 则称系统(1)在集合S中的每一点处都有度量正则性.

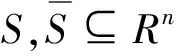
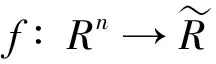
注1[8]A为几乎凸集且riA=Ø， 则riA和clA为凸集.

2 主要结果

S∶={x∈D|h(x)≤0}非空， 考虑以下结果：

(ⅰ)系统(2)具有全局误差界.

(ⅱ)系统(2)在任意非空集合Ŝ⊂S上具有度量正则性.

(ⅲ)系统(2)在集合S上有度量正则性.

(ⅳ)系统(2)在集合S内每一点处都有度量正则性.

(ⅴ)系统(2)满足Slater条件.

则以下关系成立：

(ⅰ)⟺(ⅱ)⟺(ⅲ)⟺(ⅳ)⟺(ⅴ)

证明在Banach空间中，Deng[4]证明了该结论成立.当x∈D∩domh，在Rn空间中，经过验证该结论仍成立.当x∈D|domh时，h(x)=+∞，[h(x)]+=+∞， 故该结论显然也成立.

clf(x)≤0，x∈clC

(3)

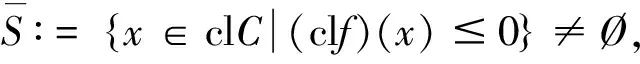
(ⅰ)系统(1)具有全局误差界.

(ⅱ)系统(1)在任意非空集合Ŝ⊂S上具有度量正则性.

(ⅲ)系统(1)在集合S上有度量正则性.

(ⅳ)系统(1)在集合S内每一点处都有度量正则性.

(ⅴ)系统(1)满足Slater条件.

则以下关系成立：

(ⅰ)⟹(ⅱ)⟹(ⅲ)⟹(ⅳ)⟸(ⅴ)

证明(ⅰ)⟹(ⅱ)：几乎凸不等式系统(1)具有全局误差界，即：存在正常数λ>0， 对于任意的x∈C， 都有d(x,S)≤λ[f(x)]+.

所以，对于任意的x∈C且满足d(x,Ŝ)≤δ， 上式也是成立的.故系统(1)在集合S的任意非空子集Ŝ上具有度量正则性.

(ⅱ)⟹(ⅲ)：已知系统(1)在集合S的任意非空子集Ŝ上具有度量正则性， 即存在正常数δ与τ(δ)， 使得

d(x,S)≤τ(δ)[f(x)]+，当d(x,Ŝ)≤δ，∀x∈C

当Ŝ=S时， 易得系统(1)在集合S上有度量正则性.

(ⅲ)⟹(ⅳ)：系统(1)在集合S上有度量正则性， 即存在正常数δ与τ(δ)， 使得

d(x,S)≤τ(δ)[f(x)]+，d(x,S)≤δ

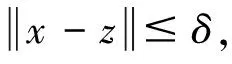
所以， 若几乎凸不等式系统(1)满足Slater条件， 则系统(1)在集合S中的每一点处都有度量正则性.

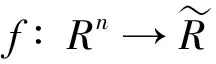
(ⅰ)凸不等式系统(3)有全局误差界⟹几乎凸不等式系统(1)有全局误差界.

(ⅴ)几乎凸不等式系统(1)满足Slater条件⟹凸不等式系统(3)满足Slater条件.

证明(ⅰ) 证明参见文献[5].

d(x,S)≤τ(δ)[f(x)]+，当d(x,S)≤δ

同理， 用类似的证明方法可以推出(ⅲ)、(ⅳ)成立.

(ⅴ)由文献[8]中引理6.3与命题6.2可知， 几乎凸不等式系统(1)满足Slater条件可以推出凸不等式系统(3)满足Slater条件.