Multisim在“自动控制原理”实验教学中的应用
2019-12-27张良,杨涛
张 良 ,杨 涛
(1.绵阳师范学院机电工程学院,四川绵阳 621006;2.西南科技大学信息工程学院, 四川绵阳 621010)
0 引言
“自动控制原理”是控制科学与工程学科的基础,是工业自动化应用的核心理论基础[1-2],也是自动化、电气工程及其自动化、测控技术与仪器等专业重要的专业基础课程[3].该课程知识涵盖面广,理论性强[4],内容抽象,涉及较多的高等数学、线性代数、复变函数等数学基础知识,学生在学习时不易接受和掌握[5-7].自动控制原理实验能够帮助学生掌握和理解控制系统分析、设计、调试方法,加深对自动控制原理课程中涉及到的稳定性、快速性、准确性、抗干扰性等问题的理解[8-10].
1 “自动控制原理”实验教学现状
绵阳师范学院机电工程学院的自动控制原理实验采用的是浙江天煌科技实业有限公司的“THKKL-6”型控制理论实验箱.学生在做实验时,直接按照实验指导书给出的实验步骤进行参数设置和电路连接,然后使用计算机上的虚拟示波器软件观察实验现象,读取系统响应曲线的性能参数和保存要求记录的实验波形.这种实验方式虽然可以加深学生对课堂理论知识的理解,在一定程度上锻炼了学生的动手能力,但是也存在一些不足[11-13]:学生按照实验步骤被动接线,对整个实验的认识仅仅停留在接线阶段,不能深入理解具体的实验电路与理论课程中相关知识点之间的联系,以至于一旦实验现象不对,便束手无策,不知道该怎么去分析和解决问题;实验箱上的元器件固化,不能扩展,只能开展验证型实验项目; 随着实验箱使用年限的增加,元器件逐渐老化,虽然按照实验指导书上的步骤正确的接线和参数设置,但实验结果误差偏大.因此,本文针对现有实验设备存在的诸多问题,提出了Multisim软件仿真和试验箱相结合的实验教学方式,以提高“自动控制原理”实验课程的教学效果,促进和培养学生通过计算机仿真来辅助控制系统调试的工程实践应用能力.
2 采用Multisim仿真实验举例
根据我院电气工程及其自动化专业自动控制原理教学大纲的要求,只讲授经典控制理论,根据这部分理论教学内容对应安排了6个实验项目,分别是:典型环节的电路模拟;二阶系统的瞬态响应;高阶系统的瞬态响应和稳定性分析;线性定常系统的稳态误差;典型环节和系统频率特性的测量;线性定常系统的串联校正.在进行实验课时,首先要求学生通过Multisim软件进行仿真完成实验,然后再使用实验箱完成实验,下面简要介绍采用Multisim软件来实现这部分实验项目.
2.1 典型环节的电路模拟
在自动控制系统中,常见的典型环节有比例环节、积分环节、惯性环节、比例积分环节、比例微分环节、比例积分微分环节.本实验要让学生采用Multisim软件模拟出以上环节,并掌握各个环节的传递函数.学生通过Multisim软件搭建各个典型环节,不仅能对典型环节建立一个直观感性的认识,还能通过参数调节,掌握各个典型环节的动态和静态特性,加深各个环节物理模型和数学模型的理解,图1就展示典型环节的Multisim模拟.一般的控制系统都是由图1中若干个典型环节有机组合而成的,因此当学生们充分理解了这些典型环节后,可以对后续的实验起到了很好的铺垫作用.

图1 典型环节的Multisim模拟Fig Multisim Simulation of Typical Links
2.2 二阶系统的瞬态响应实验举例
在分析和设计自动控制系统时,常常把二阶系统的瞬态响应特性做为一种基准[14],因此二阶系统的瞬态响应分析就显得特别重要.
2.2.1 理论分析 典型二阶系统的闭环传递函数为
(1)
(2)

(3)
针对不同的ζ值,特征根会出现下列四种情况:
1)欠阻尼:0<ζ<1
(4)
(5)
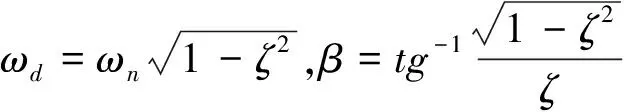
2)临界阻尼: ζ=1
S1,2=-ωn
(6)
C(t)=1-e-ωnt(1+ωnt)
(7)
此时,系统的单位阶跃响应是一条单调上升的指数曲线.
3)过阻尼: ζ>1
(8)
此时系统有二个相异实根,它的单位阶跃响应包含两个单调衰减的指数项,也是一条单调上升的指数曲线.
4)无阻尼: ζ=0
S1,2=±jωn
(9)
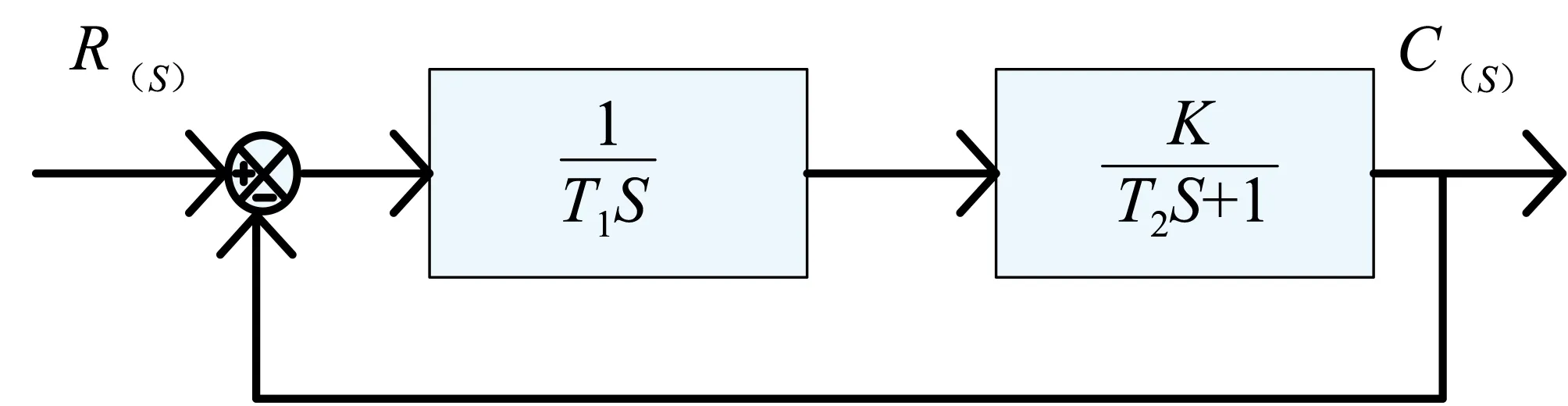
图2 二阶系统方框图Fig.2 Block Diagram of Second-order System
此时,系统的单位阶跃响应是一个等幅振荡曲线.
2.2.2 仿真建模 典型的二阶系统结构方框图如图2所示.根据方框图可以看出典型的二阶系统是由惯性环节和积分环节组成.
由图2可以得到该二阶系统的开环传递函数为:
(10)


图3 二阶系统的模拟电路图Fig.3 Analog Circuit Diagram of Second-order System
图中:R1=R2=R3=R6=R7=200kΩ
R4=R5=R=100kΩ
C1=C2=C=1μF,Rx是可调电阻,T1=R5C2=RC,T2=RxC1=RxC
闭环传递函数为:
(11)
与典型二阶系统的闭环传递函数(1)式对比可得:
(12)
(13)
2.2.3 仿真分析 在ωn值一定时,给系统输入单位阶跃信号,观察不同ζ值的实验曲线.
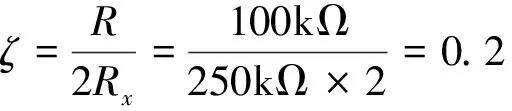


图4 ζ=0.2时系统的单位阶跃响应Fig.4 Unit Step Response of the System at ζ=0.2图5 ζ=0.707时系统的单位阶跃响应Fig.5 Unit Step Response of the System at ζ=0.707



图6 ζ=1时系统的单位阶跃响应Fig.6 Unit Step Response of the System at ζ=1图7 ζ=2.5时系统的单位阶跃响应Fig.7 Unit Step Response of the System at ζ=2.5
2.3 高阶系统稳定性分析实验举例
2.3.1 理论分析 在实际的控制工程中,绝大部分控制系统都是三阶及三阶以上的系统,这类系统称之为高阶系统.在进行高阶系统的稳定性判断时,常常采用Routh或Hurwitz这两种代数稳定判据方法.这两种判断方法的本质是相同的,都是根据相同特征方程的系数来判断特征根在s平面的位置,从而判断系统的稳定性.
2.3.2 仿真建模 下面研究一个三阶系统的稳定性和系统参数K的变化对系统性能的影响情况.三阶系统的方框图如图8所示,根据方框图可以看出该二阶系统是由两个惯性环节和一个积分环节组成,因此,通过典型环节电路模拟,可以很容易的得到二阶系统的模拟电路图如图9所示.

图8 三阶系统方框图Fig.8 Block Diagram of Third-order System

图9 三阶系统的模拟电路图Fig.9 Analog Circuit Diagram of Third-order System
由图3可以得到该二阶系统的开环传递函数为:
(14)
式中:
T=R4×C3=100kΩ×10μF=1S
T1=R2×C1=100kΩ×1μF=0.1S
T2=R3×C2=500kΩ×1μF=0.5S

S3+12S2+20S+20K=0
由Routh判据得:
K>12 系统不稳定
K=12 系统临界稳定
0 2.3.3 仿真分析 给系统输入单位阶跃信号,取不同的K值观察系统实时输出曲线. 图10 K=2时系统的单位阶跃响应Fig.10 Unit Step Response of the System at K=2图11 K=12时系统的单位阶跃响应Fig.11 Unit Step Response of the System at K=12 图12 K=20时系统的单位阶跃响应Fig.12 Unit Step Response of the System at K=20 在“自动控制原理”实验教学中引入Multisim 软件,加深了学生对电子CAD软件的灵活运用,提高了学生的动手能力,克服了传统“按图接线”硬件实验的不足,增强了实验与理论课程知识点之间联系的理解,清楚了实验原理、实验方法和实验结论的关系,实现了“自动控制原理”实验课程的教学目的与效果,也初步培养了学生通过计算机仿真辅助控制系统设计和调试的工程实践应用能力.


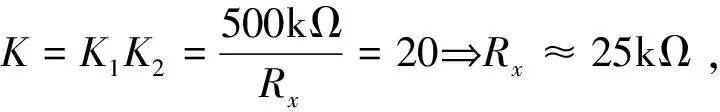
3 结论
