关于有序分拆的分部量1的几个In-place恒等式

郭育红,马蕾

(河西学院数学与统计学院,甘肃 张掖 734000)

1 引言

在经典的分拆理论中,对于分拆恒等式的研究一直是一个热点问题[1-3].近年来,文献[4-12]得到了丰富的研究成果.特别是,文献[4]建立了下面的恒等式.

定理 1.1[4]正整数n的无序分拆中偶分部量出现偶数次的分拆数等于正整数n的分部量不是4m+2型的无序分拆数.

开展白花前胡留种技术研究和优质种子培育技术研究从而实现有效控制早期抽薹率是未来值得重点关注的研究方向，不但对中药资源的开发利用具有重要意义，而且能为开展优良中药材品种选育研究提供理论支撑。

文献[13]给出了关于正整数的有序分拆的相应恒等式.

定理 1.2[13]设n≥0,则正整数n的有序分拆中偶分部量出现In-place偶数次的分拆数等于正整数n的分部量不是4m+2型的有序分拆数.

定理 1.3[13]设n≥0,则正整数2n的有序分拆中奇分部量出现In-place偶数次的分拆数等于正整数n的每个奇分部量有两种形式的有序分拆数.

孕妈妈可以根据自己的体能和身体状况安排游泳时间，通常每周1～2次。对孕妈妈来说，游泳环境的清洁和安全尤为重要，选择水质干净合格的游泳场所，避免病菌感染而影响妊娠结局。

定理 1.4[13]设k≥2,l≥2是给定的整数.设n≥0,则正整数n的有序分拆中能被k整除的分部量出现In-place次数是l的倍数的分拆数等于正整数n的分部量不是lkm+ik(其中:1≤i≤l−1)型的有序分拆数.

定理 1.5[13]设k≥2是给定的整数.设n≥1,则正整数kn的有序分拆中不能被k整除的分部量出现In-place次数是l的倍数的分拆数等于正整数n的不能被k整除的分部量有两种形式的有序分拆数.

该次数据采用SPSS 14.0统计学软件分析，组间计数资料[n（%）]和计量资料（±s）分别行 χ2检验和 t检验，P<0.05为差异有统计学意义。

2016年,本文作者研究了关于分部量是1,2的有序分拆的In-place恒等式,给出了下面的结论.这里把分部量是1,2的有序分拆记为“1-2有序分拆”.

定理 1.6[14]设n≥1,则正整数n的1-2有序分拆中分部量2出现In-place偶数次的分拆数等于正整数n+1的分部量不是4m+3型的有序分拆数.

进而研究回文的有序分拆的 In-place恒等式.所谓回文的有序分拆[1]是指一个有序分拆从左边读和从右边读是相等的.例如,4的回文有序分拆有:(4),(2,2),(1,2,1),(1,1,1,1).关于回文的有序分拆的In-place恒等式,有以下结论.

综合各方面因素,两种方案比较,方案2较理想，采用变频发电技术，使江都三站电机效率得以提高,同时有利于长期抽水运行，也可减小电机体积和重量，节约投资。

在这段语料中，从宾利先生对本内特太太提议的回答可以看出，宾利先生的话语中存在着明显的语用模糊现象。宾利先生想要达西先生和伊丽莎白两个人单独出门。但是他询问的却是伊丽莎白的妹妹 （Kitty）是否觉得路程太远了。这种语用模糊的现象，通常使得话语的言外之意的不确定性带有一定的动机。一方面为达西先生和伊丽莎白的独处创造了条件，另一方面又从礼貌原则出发保存了伊丽莎白妹妹在对话中的面子。

上述恒等式是定理2.2及正整数的没有限制的有序分拆数的直接结果.这里给出一个组合证明.

自然地,得到下面的恒等式.

西双版纳国家公园的建设是基于上世纪八十年代成立国家级自然保护区，九十年代保护区也尝试在小范围采用“社区共管”的方式来缓解发展与保护的矛盾，但浅尝辄止。随着西双版纳大规模的引入橡胶种植，周边社区的经济收入得到较大改善，对保护区和国家公园的依赖也大大降低，对资源权利的诉求较弱，主要是希望国家公园的建设也能带动本村旅游业发展。

本文继续沿用学者们采用的术语 “In-place”.所谓有序分拆的一个分部量出现In-placej次是指该分部量出现在连续的j个位置上.

例如,有序分拆(2,2,2,2,3,4,5,6,6,2,2,3,1,1)中,每个偶分部量出现In-place偶数次,而奇分部量出现的次数有奇数次,也有偶数次.文献[13]把奇分部量有两种形式中的一种形式表示为带“*”号.本文仍然采用这种表示方法.

本文首先给出正整数的有序分拆中的分部量1有两种形式的一个恒等式.其次得到了几个关于正整数的分部量是1或者2的有序分拆数以及回文的有序分拆数的In-place恒等式.

2 几个In-place恒等式

首先给出下面关于分部量1的一个In-place恒等式.

定理 2.1设n≥1,则正整数n的有序分拆中分部量1有两种形式的分拆数等于正整数2n的分部量1出现In-place偶数次,且不含大于1的奇分部量的有序分拆数.

证明证明类似于文献[13],对于正整数的分部量1有两种形式的任一个有序分拆C,作如下的变换:

•把大于1的分部量λ变换成2λ;

•把没有标“*”号的分部量1变换成2;

《萨蒂钢琴曲全集（第二版）》，CD6张，商标：Warner Classics/Parlophone，唱片号：B07CQL32G3，发行日期：2018年8月24日。演奏：阿尔多·齐科里尼。埃里克·萨蒂的钢琴作品充分体现了他作为创作者的独特声音，包括幽默和模仿神秘主义和宗教色彩。对于这些神秘的作品，阿尔多·齐科里尼的诠释是无可替代，他对萨蒂音乐的善变情绪和幽默感非常敏感，没有人能像他那样出色地演绎萨蒂。当音乐需要时，他会以纯洁、细腻和力量的完美融合来演绎作品。

例 2.1设n=3,则正整数3的分部量1有两种形式的有序分拆有下面13个:

按照上述变换,得到正整数2n的一个有序分拆,在该有序分拆中,分部量1总是成对出现,即分部量1出现In-place偶数次;而且该有序分拆中没有大于1的奇分部量.

[26][28]哈贝马斯：《在事实与规范之间》，童世骏译，北京：生活·读书·新知三联书店，2003年，第148、379-380页。

上述变换显然是一一的,故结论成立.证完.

给出一个例子来说明定理2.1中的对应关系.

•把标有“*”号的分部量1变换成1,1.

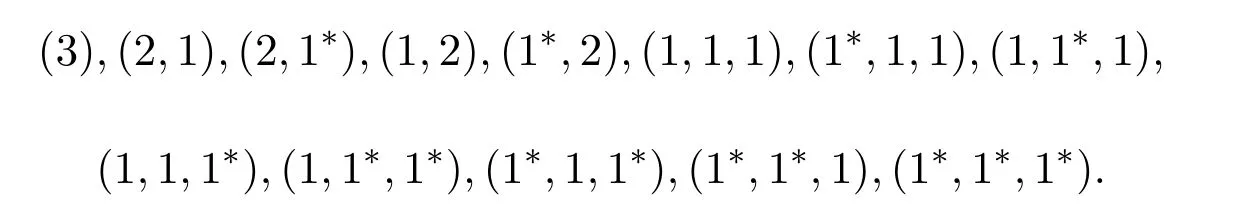
6的分部量1出现In-place偶数次,且不含大于1的奇分部量的有序分拆有下面13个:

尽管市场不断扩大、业务不断增长，IoT仍处于技术发展的初期，依旧面临一系列的安全隐患，庞大的数量和自身的脆弱性使得IoT设备极易成为黑客的首选目标。电影《速度与激情8》中数以万计的智能车辆被“天眼”系统恶意操控，进而组成“僵尸车联网”围剿国防部长；再如，2016年下半年，Mirai病毒控制超过30多万台的IoT设备对Dyn公司、OVH公司发动大规模分布式拒绝服务（DDoS）攻击，致使164个国家或地区受到影响。因此，IoT产业化的日益加速与技术的安全可信之间的矛盾成为该领域急需解决的重要问题，也是推动新型IoT技术发展的重要因素之一。

由定理2.1的证明很容易得到下面关于1-2有序分拆的In-place恒等式.

定理 2.2正整数2n的1-2有序分拆中分部量1出现In-place偶数次的有序分拆数等于2n.

证明如果在有序分拆中,分部量1有两种形式,则正整数n的分部量均为1的有序分拆(1,1,···,1)产生2n个有序分拆.于是按照定理2.1中的变换,这2n个有序分拆对应2n的1-2有序分拆,而且分部量1出现偶数次.证完.

并且,他们将上述恒等式做了推广,得到了较为一般的结论.

伴随企业的运行及发展，在企业集团运行中，战略性成本管理作为较为重要的内容，是企业经济发展的保障。在企业运行中，若只是依靠短期成本降低是无法满足企业发展需求的。在成本管理中，应该结合成本管理的理念，转变以往的成本核算以及成本经营控制机制，结合企业成本管理工作的特点，进行成本管理策略的完善，逐渐提高企业的经济性，为企业成本功能、成本质量以及成本管理的制度完善提供参考。

定理 2.3正整数2n的1-2有序分拆中分部量1出现In-place偶数次的有序分拆数等于正整数n+1的有序分拆数.

定理 1.7[14]设n≥1,则正整数n的1-2回文有序分拆中分部量2出现In-place偶数次的分拆数等于正整数n+1的分部量不是4m+3型的回文有序分拆数.

对于(B)中的任意一个分拆,首先按照从右到左的顺序把2和它左边连续的分部量1相加得到新的分部量,得到2n的分部量是偶数的有序分拆.然后,把每个分部量除以2,就得到n的有序分拆.最后,给得到的n的有序分拆的右端添上分部量1,于是得到n+1的右端分部量是1的有序分拆.

(A)右端的分部量是1;

(B)右端的分部量是2.

对于时间要素(见图2),事件e19和事件e20都是在时间编号为t19的时间段内发生的,这时就在事件e19的属性tid中同时标注出t20.

对于(A)中的任意一个分拆,首先按照从左到右的顺序把连续的分部量1和它右边的2相加得到新的分部量,得到2n的分部量是偶数的有序分拆.然后,把每个分部量除以2,就得到n的有序分拆.最后,给得到的n的有序分拆的右端分部量加上1,于是得到n+1的右端分部量是大于1的有序分拆.

证明(组合证法)将正整数2n的1-2有序分拆中分部量1出现In-place偶数次的有序分拆分为下面两类:

综上,可得到n+1的所有有序分拆.反之亦然.证完.

城区学校规模大，师资充足，能够做到开齐学科，开足课时；但市郊农村学校重文化轻素养，认识偏颇,艺术教师配备情况远低于城镇学校，师资严重缺乏且多为兼职、专职，专业的艺术教师甚少而且人员流动大，主课老师兼职情况也比较普遍。具体表现在：

给出一个例子来说明定理2.3中的对应关系.

(1) Research on the teaching function of UltraLab network experiment

例 2.2设n=3,则6的1-2有序分拆中分部量1出现In-place偶数次的有序分拆与正整数4的有序分拆之间的对应关系如下:

当然,由定理2.3的证明很容易得到下面的恒等式.

推论 2.1正整数 2n的 1-2有序分拆中第一个分部量是 1,且分部量 1出现In-place偶数次的有序分拆数等于正整数n的有序分拆数.

推论 2.2正整数 2n的 1-2有序分拆中最后一个分部量是 1,且分部量 1出现In-place偶数次的有序分拆数等于正整数n的有序分拆数.

推论 2.3正整数 2n的 1-2有序分拆中第一个分部量是 2,且分部量 1出现In-place偶数次的有序分拆数等于正整数n的有序分拆数.

推论 2.4正整数 2n的 1-2有序分拆中最后一个分部量是 2,且分部量 1出现In-place偶数次的有序分拆数等于正整数n的有序分拆数.

接下来,考虑回文的有序分拆,得到下面的恒等式.

定理 2.4正整数2n的1-2有序分拆中分部量1出现In-place偶数次的回文有序分拆数等于正整数n+1的回文有序分拆数.

定理2.4的证明类似于定理2.3,故略去.这里给出一个例子来说明定理2.4.

例 2.3设n=3,则正整数 6的分部量 1出现 In-place偶数次的有序分拆有下面 4个:(2,2,2),(1,1,1,1,1,1),(1,1,2,1,1),(2,1,1,2).而4的回文有序分拆是:(1,1,1,1),(4),(2,2),(1,2,1).