空间分数阶半经典Schrödinger方程解的高振荡行为

孙苏珍,王冬岭

(西北大学数学学院,陕西 西安 710127)

1 引言

经典Schrödinger方程是量子力学中的一个基本方程,也是量子力学的一个基本假定,它描述了微观粒子的状态随时间变化的规律.半经典量子力学界于经典物理和量子物理之间,运用到了量子力学量子化的概念,但同时并没有摒弃经典物理中的一些理念,是经典力学过渡到量子力学中的产物.在半经典量子力学中,物质运动状态有一条近似的经典轨迹,同时也会受到不可忽略的量子效应扰动.从数学方程角度来看,由于单个粒子的状态高度集中在某条近似经典轨迹的附近,波函数会在局部形成强烈的高振荡,即半经典 Schrödinger方程的解具有局部高振荡特征.对于半经典Schrödinger方程的研究,文献[1-7]在这方面做了很多工作.

整数阶Laplace方程基于经典的布朗运动假设,分数阶Laplace方程基于粒子运动的 Lévy过程,Lévy过程有利于刻画粒子的非局部特征,于是许多学者开始重视研究分数阶 Laplace方程.文献 [8]利用 Rieze位势给出了 (−∆)s的定义,至此人们开始对分数阶Laplace方程展开了丰富的研究并获得了大量成果.文献[12]给出了分数阶Laplace算子基本解,为之后研究分数阶Laplace方程解的性质奠定了基础.文献[9]给出了(−∆)s的最大值原理,文献[10]研究了分数阶Laplace方程解的正则性.目前,分数阶Laplace算子在自然科学领域已经有了重要的应用.分数阶导数是一个非局部算子,与整数阶微分方程相比,能更好地描述具有长程效应的物理现象和动态过程.

首先简单介绍几种分数阶Laplace的定义方法[11]:

(i)定义在Rn上的分数Laplace算子是一个具有非局部性的拟微分算子,形式如下:

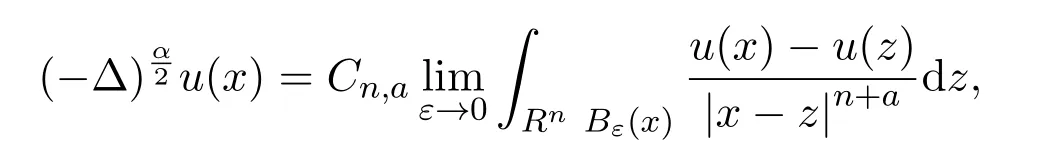
其中α∈(1,2)是任意实数,Cn,a是依赖于空间维数n和α的常数,该算子定义在S空间,即由Rn光滑速降函数构成的Schwarz空间.

(ii)在S空间中,也可以用Fourier变换来等价地定义分数阶Laplace算子:

其中F(u)是u的Fourier变换.当α=2时,分数Laplace算子退化成经典的Laplace算子,当1<α<2时,该分数阶Laplace算子为非局部算子.

(iii)还可以将算子延拓到广义函数空间

其中该空间内积定义如下

(iv)还可以通过考虑在Rn×[0,+∞)的以下问题来定义Laplace算子:

其中C=C(n,a)是一个合适的正常数,详见文献[12].本文用Fourier变换来定义分数阶Laplace算子.

选择谱方法(Galerkin谱方法[13]和拟谱方法[1-2])作为求解 Schrödinger方程的首要数值方法,主要是因为谱方法有高精度,并且Schrödinger方程本身具有谱算子特征.分裂算法是微分方程计算中常用到的一种方法,它将原方程分裂成几个更简单的方程,然后通过某种组合方式来构造出原方程的数值算法.分裂算法和拟谱算法的结合,可以同时具备显格式,高精度,保结构的特点.由于Schrödinger方程在空间方向是线性的,可以直接用谱方法进行空间离散变成线性常微分方程,并且势函数可以精确求解,所以用分裂谱方法来求解Schrödinger方程有很明显的优势.

本文主要通过分裂谱算法把文献[14]中关于半经典整数阶Schrödinger方程解的高振荡行为推广到空间分数阶Schrödinger方程,并通过数值比较研究空间分数阶阶数α对解的高振荡行为的影响.

2 整数阶半经典 Schrödinger方程

考虑d(d≥1)维线性 Schrödinger（LS）方程:

其中u=u(x,t)是关于空间变量x和时间变量t的波函数,i是虚数单位,~是普朗克常数,V=V(x)是势函数,(x,t)∈R+×Ω,Ω⊂Rd是波函数在空间中的定义域.在线性 Schrödinger方程中,当常数很小时,即 0<≪1,则称其为半经典 Schrödinger方程.半经典Schrödinger方程的解在局部具有高振荡性质.

半经典的 Schrödinger方程在许多应用中起着核心作用,是量子力学的基本模型[15].具有时间依赖势的Schrödinger方程在量子物理学和理论化学中具有重要意义,考虑具有时间依赖势的半经典Schrödinger方程的初值问题[14]

初值条件u(x,0)=u0(x),其中V是一个实值的,具有时间依赖的势函数,0<ε≪1是半经典参数.

(1)式描述了一个由电子和一个更大质量的粒子或粒子系统组成的系统,例如原子核或原子晶格,具有相互作用势V,ε是电子和质量更大的系统质量之比的平方根.由于方程(1)是线性的,可直接对空间变量半离散化,将其转化为线性ODE方程,然后通过计算矩阵指数来求解.但其中半经典参数ε的微小变化会引起解的快速震荡,因此给数值离散带来了很大的困难,解决这些困难既需要算法的灵活性也需要对原方程解的结构进行一定的分析和理解.一个很好的方法是用分裂谱方法,因为Schrödinger方程在空间方向是线性的,可以直接用谱方法进行离散变成线性方程,并且分裂谱方法对整数阶和分数阶都有优势,从而避免了分数阶算子的非局部特征差分离散导致的满矩阵带来的计算量增加.

3 空间分数阶半经典 Schrödinger方程

4 数值试验与分析

4.1 一维例子

根据上面的数值方法,首先考虑一维的数值例子,其中V(x)=2x2,初值条件

取x=[−π,π],N=1000,t=[0,0.5],M=500,通过分裂谱方法对空间分数阶半经典 Schrödinger方程进行数值计算,下图为数值解u(x,t)及Re(u(x,t)),Im(u(x,t))的图像,其中取各种参数ε,α进行比较分析.

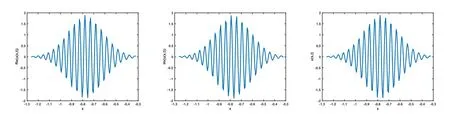
图 1 取 ε=10−2,α=2时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

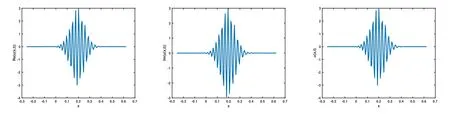
图 2 取 ε=10−2,α=1.8时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

图3 取ε=10−2,α=1.6时对应的Re(u(x,t)),Im(u(x,t),u(x,t)图像

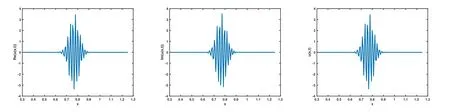
图4 取ε=10−2,α=1.2时对应的Re(u(x,t)),Im(u(x,t),u(x,t)图像

图5 取 ε=10−4,α=2时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

图6 取ε=10−4,α=1.6时对应的Re(u(x,t)),Im(u(x,t),u(x,t)图像

从图1-图6可以看到,通过与整数阶薛定谔方程的比较,当α不断变小时,波函数在空间方向的振荡频率增高,振荡宽度变小,峰值变大.说明空间分数阶算子的阶数α对于解的高振荡特征具有明显而直接的影响.空间分数阶算子的非局部特征具有使得解的振荡聚集的效应.改变势函数为V(x)=1+cos(x),其他条件和上面例子相同,分别取不同的α,对应计算结果的图像如下,从图中不难发现和上面类似的结果,即空间分数阶算子对于解的高振荡产生显著的影响和聚集效应.

图7 取ε=10−1,Re(u(x,t))在α=2,1.95,1.9的图像

图 8 取 ε=10−1,Re(u(x,t))在 α=1.85,1.8,1.75的图像

图 9 取 ε=10−1,Re(u(x,t))在 α=1.7,1.6,1.2的图像

图10 取 ε=10−3,α=2时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

图 11 取 ε=10−3,α=1.6时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

图 12 取 ε=10−3,α=1.2时对应的 Re(u(x,t)),Im(u(x,t),u(x,t)图像

4.2 二维例子

进一步考虑二维空间分数阶半经典Schrödinger方程的例子

其中 Ω=[−4π,4π]2×(0,T],取T=4,N=250,M=400,同样用分裂谱方法对其进行数值计算,分别取α=2,1.6,1.2,下图为数值解及其等高线图像.

图13 取 ε=10−1,u(x,t)在α=2,1.6,1.2的数值解

图14 取ε=10−1,u(x,t)在α=2,1.6,1.2数值解的等高线图

图15 取 ε=10−2,u(x,t)在α=2,1.6,1.2的数值解

图16 取ε=10−2,u(x,t)在α=2,1.6,1.2数值解的等高线图

图17 取 ε=10−6,u(x,t)在α=2,1.6,1.2的数值解

图18 取ε=10−6,u(x,t)在α=2,1.6,1.2数值解的等高线图

对于二维情况,从计算结果可以看出,空间分数阶算子对于解的振荡也产生了明显而直接的影响.当参数ε相对较大时,空间分数阶算子对于解的振荡的区域有着非常敏感的影响,随着α的变小,振荡区域开始扩散,振荡的区域变大.但是当参数ε相对较小时,空间分数阶算子对于解的振荡的区域的敏感性降低,随着α的变小,振荡区域变小,振荡特征逐步减弱,此时的分数阶算子表现出光滑效应,即逐步消除振荡的效果.当参数继续变小取ε=10−6时,数值解基本上不再具有明显的振荡特征.