半环上的素同余和同余的根

吴亚楠,任苗苗

(西北大学数学学院,陕西 西安 710127)

1 引言

众所周知,同余在代数的研究过程中扮演着非常重要的角色.文献[1]通过类比交换环上的理想,引入了可换加法幂等元半环的素同余的概念,且完整地描述了tropical半域T,半域Zmax和二元半域B上的多项式半环和Laurent多项式半环的素同余.

定义 1.1设(S,+,·,0,1)是(2,2,0,0)型代数.若S满足下列条件:

(1)(S,+,0)是可换幺半群;

(2)(S,·,1) 是幺半群;

(3)(∀a,b,c∈S)a(b+c)=ab+ac,(a+b)c=ac+bc;

(4)(∀a∈S)a·0=0·a=0;

则称S是半环[2].进一步,若(S,·)是交换半群,则称S是交换半环.接下来给出交换半环上同余的概念.

定义 1.2设S是交换半环,ρ是S×S的子集.若对于任意a,b,c,d∈S,

(1)(a,a)∈ρ;

(2)(a,b)∈ρ蕴含着 (b,a)∈ρ;

(3)(a,b),(b,c)∈ρ蕴含着 (a,c)∈ρ;

(4)(a,b),(c,d)∈ρ蕴含着 (a+c,b+d)∈ρ;

(5)(a,b),(c,d)∈ρ蕴含着 (ac,bd)∈ρ,

则称ρ是S上的同余.

容易验证,{(a,a)|a∈S}是S上最小的同余.称其为平凡同余,记为∆.另一方面,S×S是S上最大的同余,称其为S上的泛同余,记为∇.若同余ρ是∇的真子集,则称ρ是S上的真同余.

定义 1.3设S是交换半环.若(S,+)是幂等元半群,则称S为可换的加法幂等元半环.

分配格和max-plus代数都是可换的加法幂等元半环的例子.以下总假设S为可换的加法幂等元半环.

定义 1.4设S为可换的幂等元半环.在S×S上定义二元运算如下:

(a1,a2)(b1,b2)=(a1b1+a2b2,a1b2+a2b1),

称上述运算为扭积运算[1].

定义 1.5设ρ,σ是S上的同余.称{αβ|α∈ρ,β∈σ}生成的同余为ρ和σ的积,记为ρσ[1].

引理 1.1[1]设ρ是S上的同余.若α∈ρ,β∈S×S,则αβ∈ρ.

定义 1.6设ρ是S上的真同余.若对于任意的α,β∈S×S,αβ∈ρ蕴含着α∈ρ或β∈ρ,则称ρ是S上的素同余[1].

定义 1.7设ρ是S上的同余.称包含ρ的所有素同余的交是同余的根,记为[1].

引理 1.2[1]设ρ是S上的同余.则

其中α=(a,b),α∗=(a+b,0),GP(α)={α∗k+(c,0))αl|k,l∈Z+,c∈S}.

定义 1.8设ρ是S上的同余.若,则称ρ是根同余[1].

本文将研究可换幂等元半环的同余.给出素同余和同余的根的一些结果,且揭示了同余ρ的根与包含ρ的素同余的全体之间的关系.

2 素同余

为了方便叙述,本文将{1,2,···,n}记为.

定义 2.1设ρ是S上的真同余.若对于S上的任意同余σ,ρ⊆σ⊆∇蕴含着ρ=σ或σ=∇,则称ρ是S上的极大同余.

命题 2.1每个可换的加法幂等元半环都有素同余.

证明假设Σ是S上的真同余的全体.易证 (Σ,⊆)是偏序集.假设{ρi}i∈I是 Σ上的链.易知是同余.现证.假设.则存在i∈I,使得(0,1)∈ρi.进一步,有∇∈ρi,与ρ∈Σ相矛盾,所以.运用 Zorn引理,得 Σ有极大同余,所以S上都有极大同余.由文献[1]可知S上的极大同余是素同余.证毕.

注 2.1S上的素同余对交运算未必封闭.例如:设S={1,0,x}是可换的幂等元半环,它的运算表如下:

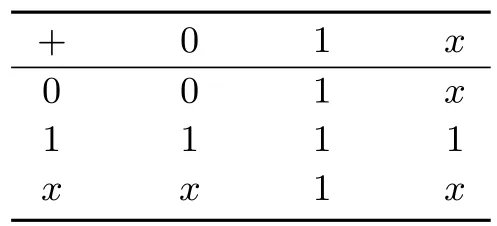
表 1 运算 “+”

表 2 运算 “·”

证明假设α是S×S上的幂零元.由定义2.2和引理 1.2得,存在k,l∈Z+,c∈S,使得 (α∗k+(c,0))αl∈∆,则 (α∗k+(c,0))αl−1α∈∆.由定义 2.3 可得,α是零因子.

注 2.2定理2.2的逆命题不成立.例如:设S={1,0,a,b}是可换的幂等元半环,它的运算表如下:

3 同余的根

致谢感谢赵宪钟教授和邵勇教授的指导.