On the nonlinear exponential sums involving the Liouville function
2019-12-26HuangJingYanXiaofeiZhangDeyu
Huang Jing,Yan Xiaofei,Zhang Deyu
(School of Mathematics and Statistics,Shandong Normal University,Ji′nan 250014,China)
Abstract:Let λ(n)be the Liouville function.The main purpose of this paper is to consider the case that β is variable and generalize the results in Sankaranarayanan and Sun,the main techniques we used is Vaughan′s identity and Perron′s formula,so we will prove a nontrivial upper bound for the nonlinear exponential sum.
Keywords: nonlinear exponential sums,Liouville function,Vaughan′s identity
1 Introduction
In analytic number theory,the problems concerning nonlinear exponential twisting arithmetic functions arise naturally in investigating equi-distribution theory,zerodistribution of L-functions and so on.We usually consider the general nonlinear exponential sum of the form
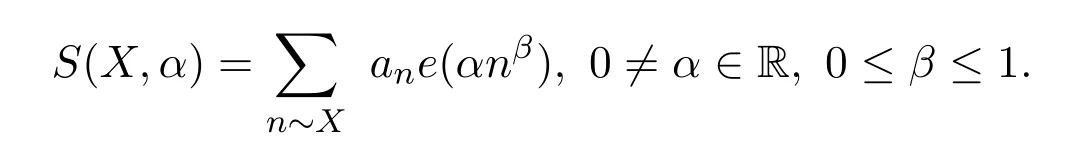
Here,n∼XmeansX≤n≤2Xande(z)=e2πiz.When,the sumS(X,α)was studied by Vinogradov for the von Mangoldt functionan= Λ(n)[1-2].Foran= Λ(n)andan=µ(n)[3-4](µis the Möbius function)the sumsS(X,α)were studied by reference[5],and it showed that these sums are intimately related toL-functions ofGL2.Iffis a holomorphic cusp form of even weight on the upper half plane,they also proved that a good upper bound of(X,α)implies a quasi Riemann hypothesis forL(s,f).Ifβis variable andanare the Fourier coefficients of automorphic forms.These sums are studied in[6-7].Reference[8]proved an asymptotic formula for the nonlinear exponential sum

wheree(z)=e2πizandk∈Z+.
For prime powerspk,the Liouville functionλ(n)is defined byλ(pk)=(−1)k.Throughout this paper,we consider the sum

As noticed in reference[9],it is amusing to point out that the hypothesis that for someθ<1,
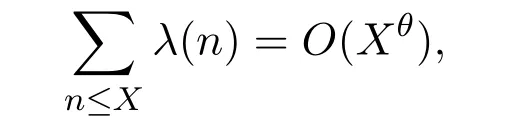
implies the quasi Riemann hypothesis.This approach is due to Polya.It should be pointed out that the Riemann hypothesis is equivalent to the view that the above estimate holds for every.Also,reference[5]considered the sums

withan≪nεfor anyε>0 andϕbeing a stabled smooth function compactly supported on R+,and under some hypothesis,it established the bound that


The main purpose of this paper is to consider the case thatβis variable and generalize the results in references[10-11].The principal aim is to prove Theorem 1.1.
Theorem 1.1Letλ(n)be the Liouville function.For any 0α∈R and 0<β≤1,for anyε>0,we have
where the implied constant depends only onε.
Remark 1.1To prove Theorem 1.1,we will apply the method in references[10-11].The main techniques we used is Vaughan′s identity and Perron′s formula.Asβis variable,for working out the dependence ofβ,we must handle the terms withβin the denominator carefully,especially in the error terms.In addition,we must choose new parameters in some place to make the method work.When,our results agree with reference[11]and improved the result in reference[10].
An analogous results can be proved whenλ(n)is replaced byµ(n).We have Theorem 1.2.
Theorem 1.2Letµ(n)be the Möbius function.For any 0α∈R and 0<β≤1,for anyε>0,we have

where the implied constant depends only onε.
Remark 1.2When,we get the upper bound estimate for our nonlinear exponential sums is.This agrees with(2)if we takefor any positive integerq,andan=λ(n)orµ(n).This is the best results so far while conjecturally the exponent ofXexpects to be.
Following references[11]and[10],we apply Vaughan′s identity forλ(n) first.For anyA,B0 andF,G,we have the formal identity:
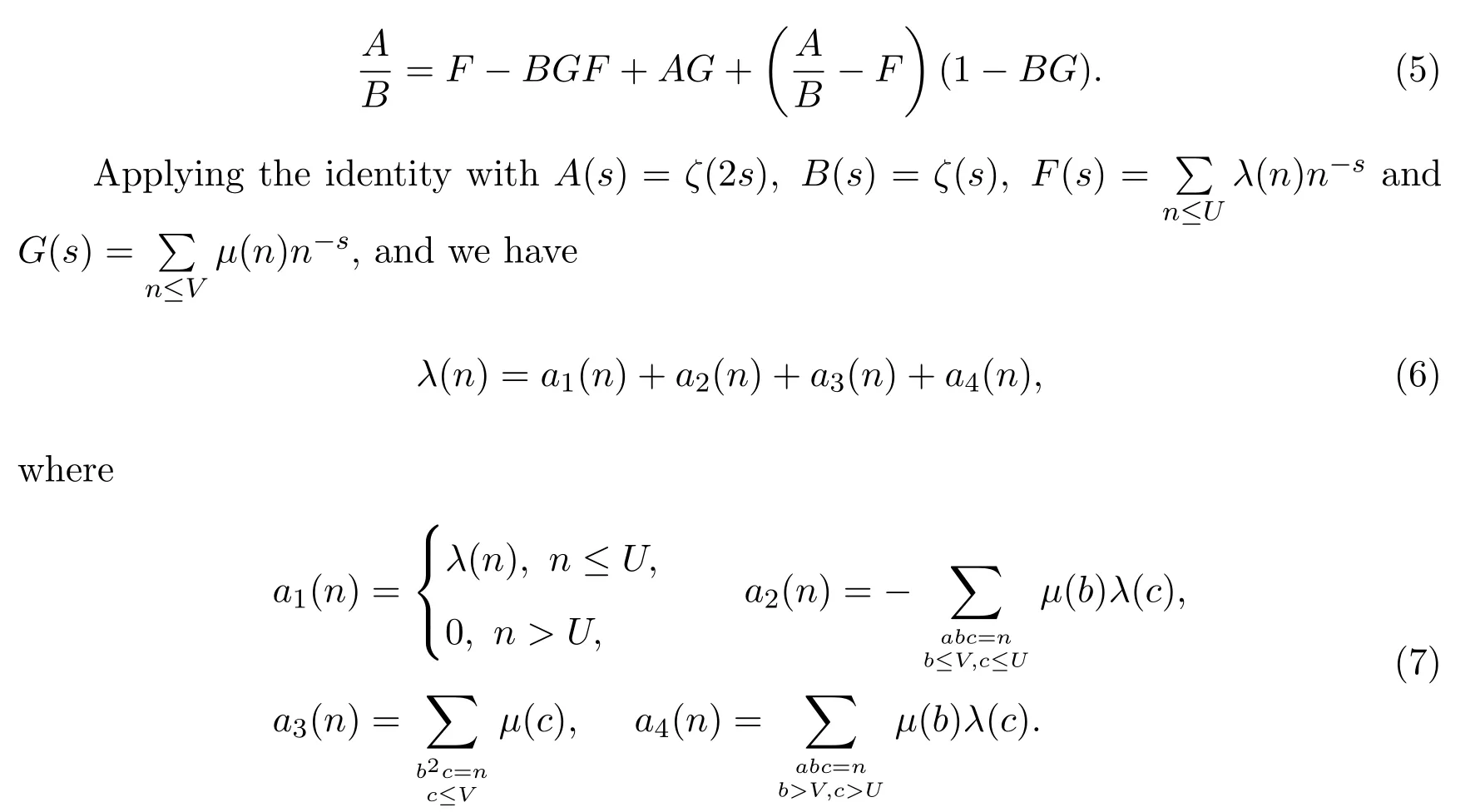
Here,U≥1 andV≥1 are free parameters to be chosen later,ζ(s)denotes the Riemann zeta-function.We have used that
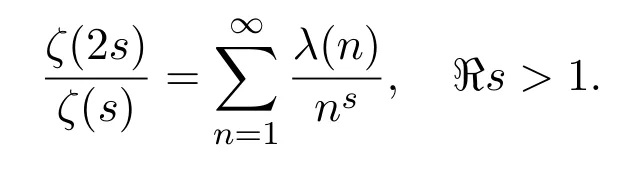
2 An application of Vaughan′s identity for λ(n)
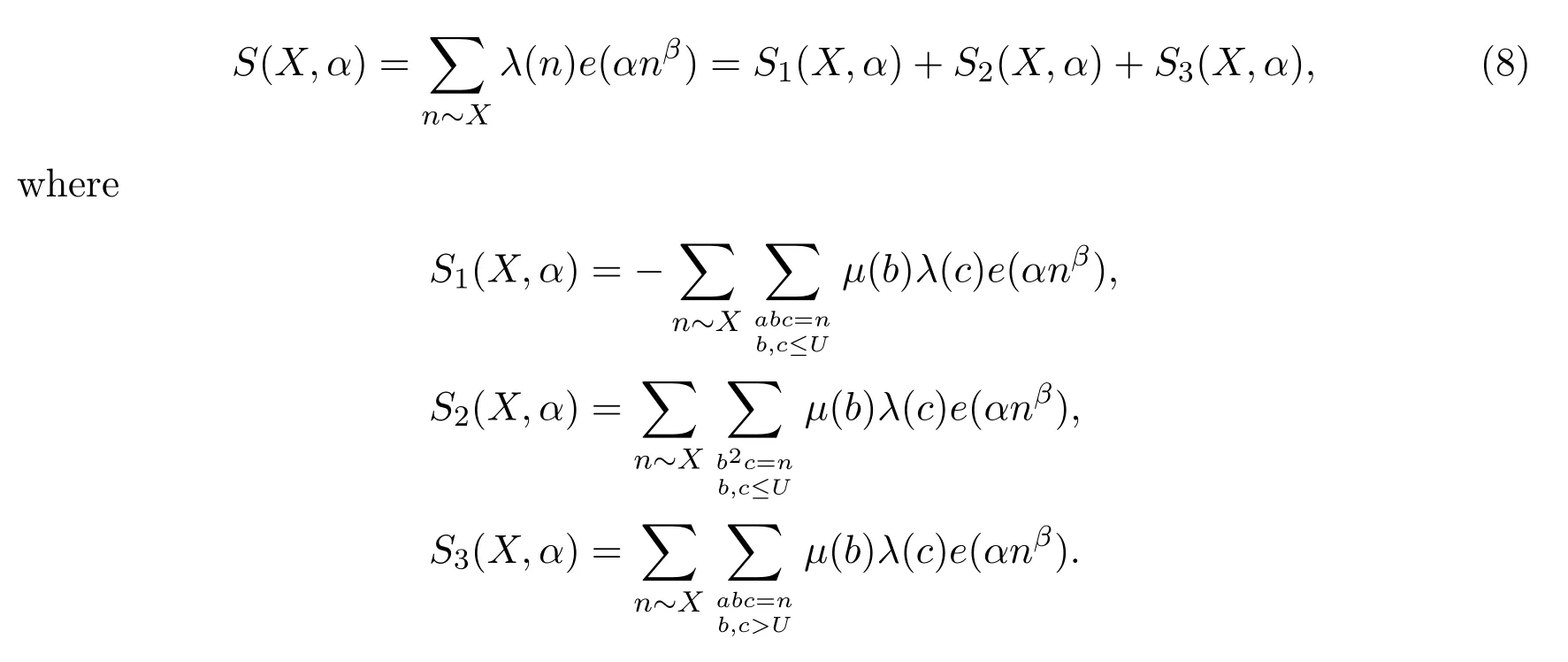

We will estimateS1,1(X,α)in Section 3 and Section 5,S1,2(X,α),S3,1(X,α)andS3,2(X,α)are of the same type and we will estimate them in Section 4.
3 Some lemmas
In this paper,we replace various exponential sums spirit in Van der Corput′s by exponential integrals and find a bound for the latter.The results from references[13]and[14]are as follows.
Lemma 3.1Letf(x)be a real-valued function,twice differentiable on[a,b]:
(1)Iff′(x)is monotonic,f′(x)≥n>0,orf′(x)≤−n<0 throughout the interval[a,b],we have
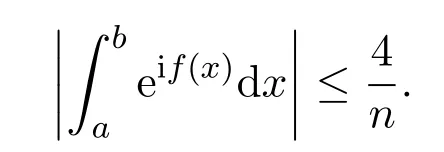
(2)Iff′(x)≥m>0,orf′(x)≤−m<0 throughout the interval[a,b],we have
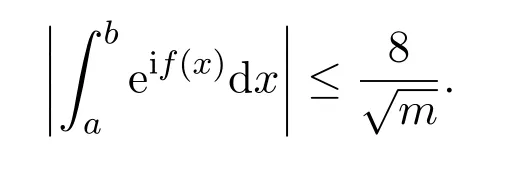
Lemma 3.2Letf(x)be a real-valued function with|f′(x)|≤1−θ|andf′(x)0 on[a,b],we have
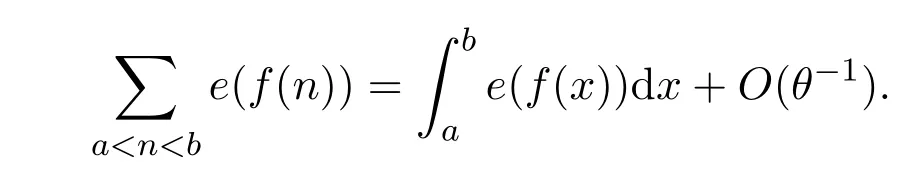
Lemma 3.3LetX,T≥1.For any complex numbersan,then
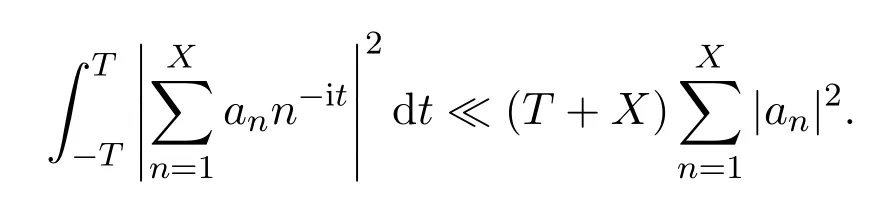
Lemma 3.4Letλandtbe real number whilex,kandβbe positive number.DefineT0=4kπ|λ|(2X)k,we have

Let|λ|≤θand setT∗=4kπθ(2X)k,then
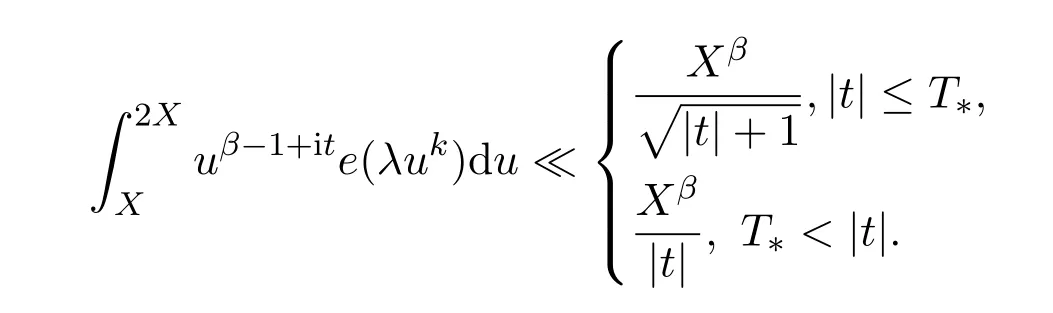
4 The estimation of S1,1(X,α)




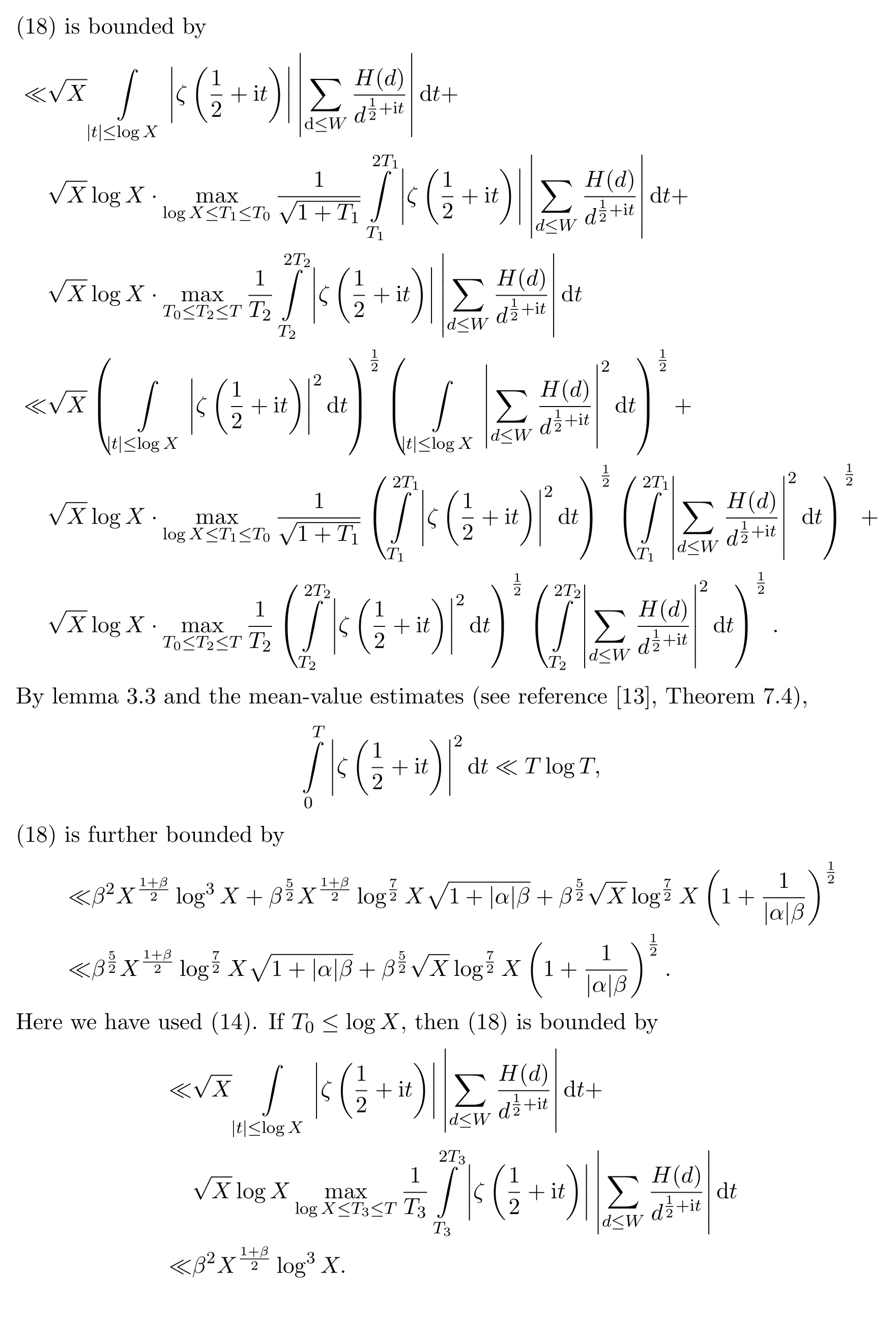

5 The estimation of S1,2(X,α),S3,1(X,α),S3,2(X,α)



6 The estimation of(X,α)and the proof of Theorem 1.1

7 Proof of Theorem 1.2

