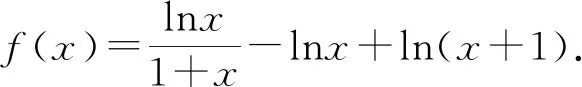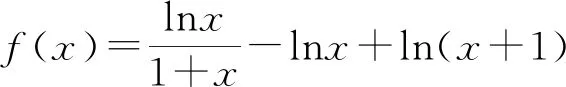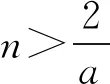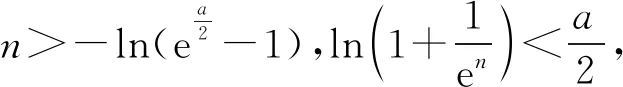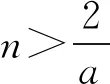揭示原有函数本质特征 助力导数综合问题解决
2019-12-26潘荣杰
潘荣杰
(北京市第八十中学 100102)
很多学生在面对导数综合题时,一般都会考虑原有函数的定义域,然后就对原有函数求导数,或根据问题情境,构造一个函数再求导数.那么为什么要求导?求导的目的是什么?所求得的导数便于后续研究吗?所研究问题的本质是要研究函数的什么性质?学生对诸多问题可能没有考虑清楚,更多的还是模式化解题.不可否认,函数的单调性是函数的最重要性质之一.导数最直接的应用就是研究函数的单调性,但不是所有的问题都要研究函数的单调性.如果需要研究函数的单调性,而导数含参数且特别复杂,分类讨论的分界点该如何确定呢?很多学生求导数之后,就陷入不知所措、无从下手、停滞不前的窘境,更谈不上找到解决问题的突破口了.
例如,2019年全国Ⅰ卷理科20题的第(Ⅱ)问,学生就遇到很大的挑战.
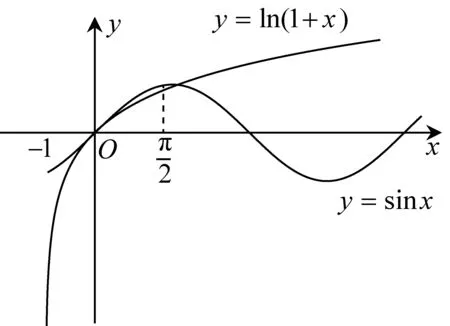
(2019年全国Ⅰ卷理20节选)已知函数f(x)=sinx-ln(1+x).
证明:f(x)有且仅有2个零点.
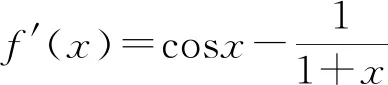
优先考虑函数的定义域,其实这就是关注原有函数的一种性质.但我们不能仅仅局限这一点,也不能求导数之后就抛弃了原有函数.我们要根据所求问题的本质,关注原有函数以及导函数的相关性质,找到问题的突破口,再利用导数这一工具解决问题.笔者结合自己的教学实践,重点谈一谈在解决函数与导数综合问题中除关注定义域外,还应关注原有函数的哪些性质?下面结合例子从四个方面加以说明.限于篇幅,所举例子均节选一个问题进行解释,以此来感受关注原有函数本身的某些性质对所研究问题带来的优化.
1 关注多项式或函数值整体的正负,明晰问题本质
关注多项式或函数值整体的正负对证明不等式、函数零点、恒成立或有解问题至关重要.
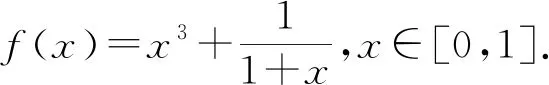
证法一
由f(x)-(1-x+x2)
得f(x)≥1-x+x2.
证法二
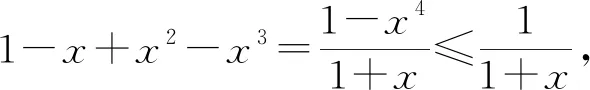
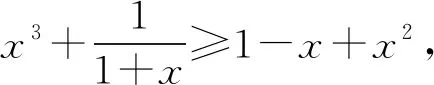
即f(x)≥1-x+x2成立.
点评本题没有用导数研究函数的最值来证明不等式,问题的解决根本就没用到导数这一工具.函数不等式的证明,不一定要构造函数,通过研究单调性等性质,再求出函数的最值达到论证的目的.函数不等式证明的数学本质还是作差,看差值的正负即可.本题根据题目的结构特征,用适当的转化、代数变形、放缩等手段就能达到论证的目标,从而问题得以快速解决.上面两种解法需要较高的数学素养,给学生带来震撼,是去除模式化的好素材.特别是“证法一”关注了f(x)-(1-x+x2)整体的正负.还有什么时候要关注多项式或函数值整体的正负呢?
例2(2016全国I卷理改编)
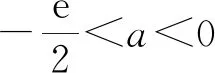
解法一
f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
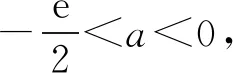

x(-∞,ln(-2a))ln(-2a)(ln(-2a),1)1(1,+∞)f'(x)+0-0+f(x)↗极大值↘极小值↗
而极大值f(ln(-2a))=-2a[ln(-2a)-2]+a[ln(-2a)-1]2=a{[ln(-2a)-2]2+1}<0.
故当x≤1时,f(x)在x=ln(-2a)处取到最大值f(ln(-2a)),且f(x)≤f(ln(-2a))<0恒成立,即此时f(x)=0无解.
而当x>1时,f(x)单调递增,至多一个零点.
综上,f(x)在R上至多一个零点,符合题意.
解法二

f(x)=(x-2)ex+a(x-1)2<0,
而f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
则f′(x)>0在(1,+∞)上恒成立,
f(x)单调递增,至多一个零点.
综上,f(x)在R上至多一个零点,符合题意.
点评函数最值或极值的正负某种程度决定该函数有无零点问题,这是零点问题的一个基本认识.解法一就是依据这个认识.但极值的正负不好判断,有时需要一定的技巧.更朴素的一个道理是:“函数在某区间上恒正或恒负,则函数在此区间上无零点”.若知道函数在某区间上恒正或恒负,就无需关注它在此区间上的单调性情况,更不用关注极值的正负,所以解法二是站在整体的角度看问题,解法当然更加简洁.在教学时,我们可以采取这种对比教学,既落实基本解法,又培养学生观察、整合、创新的意识,使学生对问题本质有更深刻的思考.
2 关注原有函数的零点,确立解题方向
零点是函数的一个重要性质,它与函数值的正负、单调区间、极值等有密切关系.
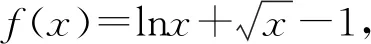

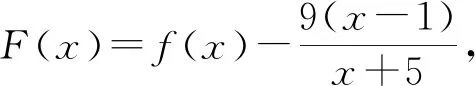
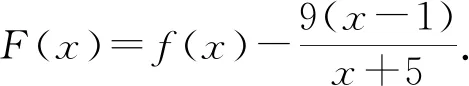
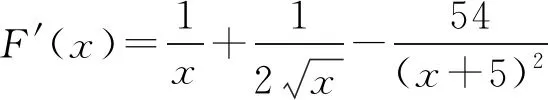
令G(x)=(x+5)3-216x(1 则x∈(1,3),G′(x)=3(x+5)2-216<0. 故G(x)在(1,3)上为减函数, 所以G(x) 即F′(x)<0在x∈(1,3)上恒成立, 故F(x)在(1,3)上为减函数. 所以F(x) 点评其实还可以去分母后,再构造函数,但不管怎样构造函数,看到了零点,就找到了解题方向,要培养学生观察零点的意识,有的函数零点可以直接看出,有时需要我们去估算原有函数或导数的零点,一般是函数的单调性与零点存在性定理相结合. (ax+1)(ex-1)-xex≤0, 设h(x)=(ax+1)(ex-1)-xex,则h(0)=0. 因为h′(x)=ex[(a-1)x+a]-a,h′(0)=0, 则h″(x)=ex[(a-1)x+2a-1]. 所以h′(x)在(0,+∞)单调递减, 故h′(x) 所以h(x)在(0,+∞)单调递减, 故h(x) 当a≥1,x∈(0,+∞)时,h″(x)>0, 所以h′(x)在(0,+∞)单调递增, 故h′(x)>h′(0)=0, 所以h(x)在(0,+∞)单调递增, 故h(x)>h(0)=0,所以a≥1不符合题意. 点评函数零点看似只是函数的一个局部性质,其实零点影响着函数的其它性质,比如函数只有一个变号零点,就知道函数在零点两侧一定异号,对我们解不等式就有很大帮助.关注函数的零点,当然也包括观察导函数的零点.本题这种寻求使命题成立的充分条件,再证明其是必要条件的解题策略在解决压轴题中很常用.在解导数压轴题过程中,也有先寻求使命题成立的必要条件,这样会缩小参数的取值范围,一般会减少分类讨论,再证明其是充分条件.此种解题策略不再举例,请读者自己体会. 例5已知函数f(x)=ex+(a-e)x-ax2,若函数f(x)在区间(0,1)内存在零点,求实数a的取值范围. 解由f(x)=ex+(a-e)x-ax2可知, f(0)=1,f(1)=0. 若函数f(x)在区间(0,1)内存在零点, 则f(x)=ex-ex+a(x-x2)≤0在区间(0,1)上有解. 设h(x)=ex-exx∈(0,1). h′(x)=ex-e<0, 故h(x)在区间(0,1)上单调递减. 所以h(x)>h(1)=0. (1)a≥0时,因为x∈(0,1),a(x-x2)≥0, 又ex-ex>0,所以f(x)>0 故此时f(x)≤0在区间(0,1)上无解. (2)a<0时,f″(x)=ex-2a>0, 则f′(x)=ex-e+a(1-2x)在区间(0,1)上单调递增. 又f′(0)=1-e+a<0,f′(1)=-a>0, 故存在x0∈(0,1),使得f′(x0)=0. 于是x∈(0,x0)时,f′(x)<0且x∈(x0,1)时,f′(x)>0. 所以f(x)区间(x0,1)上单调递增, 所以f(x0) 所以f(x)=ex-ex+a(x-x2)≤0在区间(0,1)上有解,a<0符合题意. 综上,a的取值范围为(-∞,0). 点评根据题目情境先观察出边界值f(0)=1,f(1)=0,根据存在零点存在定理,函数值必然存在小于等于零的值,这也是对零点问题的最朴素认识.有了这种认识,问题得以转化为不等式有解问题.不等式有解问题一定要关注函数值的正负,而关注函数值的正负,就找到了分类讨论的分界点,正是由于关注了原有函数的一些性质,问题才得到了完美解答. 解易证f(x)=acosx+xsinx为偶函数. f′(x)=-asinx+sinx+xcosx =(1-a)sinx+xcosx>0, 由f(x)是偶函数可知,f(x)有两个零点. 综上,当a>0时,f(x)的零点个数为0;当a=0时,f(x)的零点个数为1;当a<0时,f(x)的零点个数为2. 点评本题不但关注了原有函数的正负,更关注了函数的奇偶性.奇偶性是一种对称性,知道自变量在原点的一侧取值时的性质,就知道另一侧的性质.如果函数有奇偶性,我们可以将自变量取值范围缩小一半,这样有助于研究导数的正负. 这里我所说的函数的边界状态可以理解为函数在定义域边界的函数值或极限. 分析我们很难直接解出不等式f(x)≥a,那么应该怎样处理?我们可以尝试观察f(x)的函数值情况,将函数f(x)整理变形后,可以看出f(x)>0在定义域(0,+∞)上恒成立,因此若a≤0,f(x)≥a的解集就为f(x)的定义域为(0,+∞).若a>0,又x→+∞,f(x)→0,说明对于给定的正数a,当x取较大值时f(x)≥a不成立,我们可以用特例加以说明. 解f(x)的定义域为(0,+∞). 所以a≤0时, 不等式f(x)≥a的解集为(0,+∞). a>0时,易证x>2时,ex>x2(证明略). 不符题意. 综上,a的取值范围为(-∞,0]. 点评本题是以极限为背景命制的,其实是考查函数值的取值情况.如何研究函数值的取值情况呢?一般通过研究函数的单调性等性质来确定值域,但本题的导数十分复杂,很难找到原有函数的单调区间,若我们关注了原有函数值的正负,关注了函数边界的极限,我们就知道f(x)的值域一定为(0,M].当然本题x→0+,f(x)→0,因此第(2)类情况也可以取较小的正数进行论证.如何说明a>0时,f(x)≥a的解集不是(0,+∞),需要对极限概念有较深刻的认识. 教学要突出数学本质,函数问题的核心就是函数性质的研究与应用.根据问题情境,我们应培养学生有意识地关注原有函数的定义域、奇偶性、函数值的正负、零点、函数的边界状态等性质,问题很可能就找到了突破口,也会使得问题更简洁更方便的解决.导数压轴问题多出在证明不等式、解不等式、恒成立或有解问题中的求参数取值范围、以及零点问题等.我们需要归类,找到一般解题思路,但我们更应关注原有函数的结构、性质,而不是一概求导解决.要突出导数的思想、工具作用,更要站在函数整体的高度认识函数问题,这是一种意识,学生一旦形成了这种意识,就会做到在一般方法与特殊策略之间灵活转化,在更高的层面去认识问题、理解问题、解决问题.这样必会有利于帮助和引导学生对数学知识本质的理解,提升学生综合创新能力,促进学生数学核心素养的形成和发展.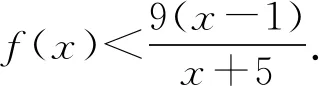
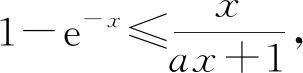
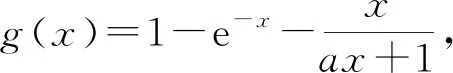
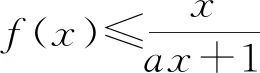
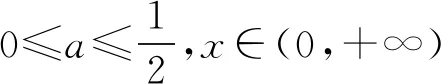
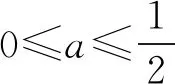
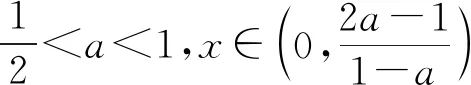
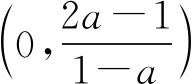
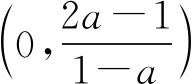
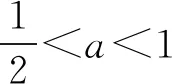
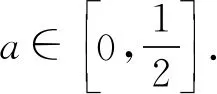
3 关注原有函数的奇偶性,降解问题难度
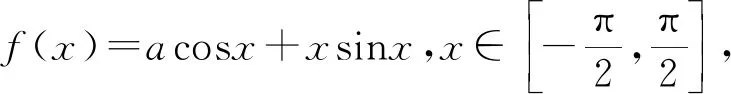
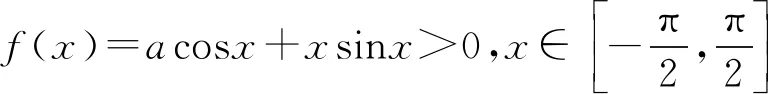
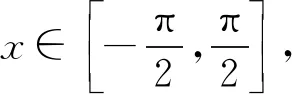
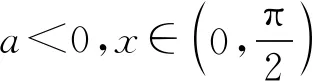
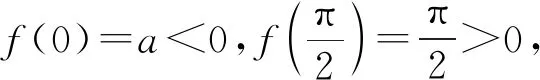
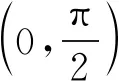
4 关注原有函数的边界状态,开阔解题视野