闵科夫斯基平面M2和闵科夫斯基变换

赵旭安

(北京师范大学数学科学学院，教育部数学和复杂系统重点实验室 100875 )

平面欧氏几何是中学数学教学的重要内容.对其中的经典结果，人们非常熟悉.而对和欧氏几何完全平行的另一种几何，闵科夫斯基几何，很多人都不了解.闵科夫斯基几何和欧氏几何有诸多相似之处，但也有一些本质的差异.利用闵科夫斯基变换可以很容易地解释狭义相对论中关于运动的参照系中所谓的尺缩和钟慢效应.本文不讨论闵科夫斯基几何的物理背景，只介绍相关的几何内容.下面为了叙述方便，我们把闵科夫斯基几何简称为闵氏几何.

平面欧氏几何是空间的几何，而平面闵氏几何是时空的几何.如果选取适当的坐标系，两个欧氏坐标都是空间坐标，而闵氏坐标同时包含时间坐标和空间坐标.爱因斯坦革新了牛顿的存在独立的时间和空间的错误认识，将对引力的研究归结为对时空几何的研究.本文也秉承这一思想，在讨论中将闵氏几何的坐标用(x,y)而不是(x,t)表示，这样也可以更好地与欧氏几何进行比较.根据Klein关于几何学的观点，研究一种几何，首先要看这种几何允许什么样的变换.因此下文会仔细介绍平面闵科夫斯基变换的概念.

1 闵科夫斯基平面M2

首先我们引进闵氏平面M2的概念.在平面上选取原点O和坐标轴x,y轴，对于向量(x,y)，定义闵科夫斯基度量d2(x,y)=x2-y2.如果这里将减号改为加号，我们的就得到欧氏度量.平面带上闵科夫斯基度量称为闵科夫斯基平面，简称闵氏平面.对于欧氏情形，d2(x,y)≥0成立，可以开方得到距离d(x,y).对于闵氏情形，d2(x,y)可以大于、小于或等于零，一般不能开方.因此可以给出以下定义.

定义1若d2(a)>0，=0或<0，则称向量a=(x,y)为类时、类光或类空向量.

类光向量a=(x,y)满足x2-y2=0，它们给出平面上过原点的两条直线，称为原点处的光锥.光锥(两条相交直线)将平面分成四部分，左右两部分中点的坐标满足x2-y2=k2>0，上下两部分中点的坐标满足x2-y2=-k2<0.

在欧氏几何中，曲线x2+y2=1称为单位圆，它是非常重要的几何对象.而在闵氏几何中，没有圆的概念.其原因在于圆在欧氏变换(平移、旋转和反射)下仍然变成圆.而这一性质在闵氏变换下不再成立.单位圆x2+y2=1的参数方程大家都很熟悉，它可以由x=cos(t),y=sin (t)给出，这里t是欧氏的角度参数.在闵氏几何下，最重要的曲线是将单位圆的方程中加号变成减号得到的单位双曲线x2-y2=1.

在欧氏情形下，我们有

引理1单位圆周x2+y2=1的参数方程为x=cos(t),y=sin (t)，这里t满足0≤t<2π.

证明设x2+y2=1，则有(x+iy)(x-iy)=1.这说明(x+iy)和(x-iy)都是单位复数.于是存在实数t使得x+iy=eit，且x-iy=e-it.根据欧拉定理eit=cos(t)+isin (t)可知引理成立.

顺便地我们得到了

和欧氏情形不同的是双曲线x2-y2=1包含两个连通分支，如果我们只选取x>0的分支，则相应的参数方程为

下面我们通过求参数方程的过程，也可以得到闵氏几何类似于角度的参数.

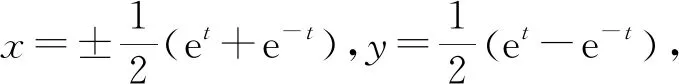
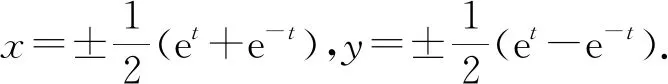
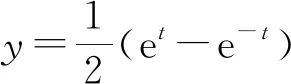
如果和欧氏情形进行比较，不难看出这里的参数t也具有某种类似角度的属性，差别是这里参数t的取值范围是整个实数轴.

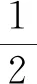
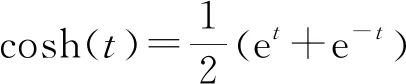
上面结果进一步说明闵氏和欧氏情形之间存在紧密的联系.对应于与三角函数的等式cos2(t)+sin2(t)=1.我们有双曲三角函数对应的结果cosh2(t)-sinh2(t)=1.

为了书写方便，下面我们把cosh和sinh简写为ch和sh.

2 闵科夫斯基变换

为了定义平面闵氏变换，我们先讨论欧氏情形是如何定义的.平面欧氏变换群Euc(2)包含平移、旋转和反射三种基本的变换.

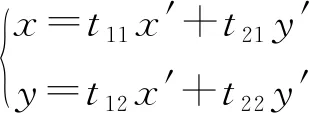
下面我们定义平面闵氏变换群Min(2).它包含平面上的平移变换群及平面上保持原点不动的子群O(1,1).这里O(1,1)称为(1,1)型的正交群.

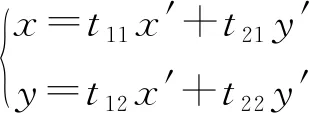
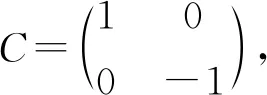
下面我们来求T的具体形式.将TtCT=C写成分量形式得到

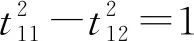
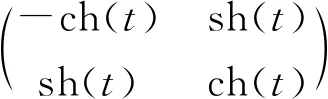
这里有四类解的原因是关于时间和空间都可以做反射.

定义5参数为t的闵氏旋转由表达式

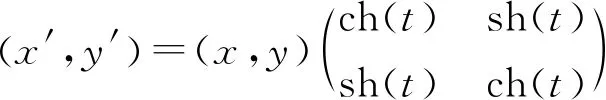
给出.对应于上面其它三种矩阵的变换分别是闵科夫斯基旋转和关于x轴、y轴的反射的复合变换和关于原点的中心对称的复合变换.

根据定义不难看出闵氏变换把平面上的双曲线x2-y2=k2，x2-y2=-k2<0和光锥保持不变.闵氏旋转可以把双曲线x2-y2=1某一分支的一点旋转至此分支上的任意其它点.平面上关于x轴的反射将坐标y变号，并且保持坐标x不变；关于y轴的反射将坐标x变号，并且保持坐标y不变.利用这两种反射及其复合变换可以把平面上一点变换到第一象限(包括边界)或者把光锥分割出的左右(或者上下)两个区域相互交换.容易验证参数为s的闵氏变换将双曲线x2-y2上参数为t的点变为参数为s+t的点.这类似于欧氏平面上的参数为θ的旋转将单位圆上参数为φ的点映为参数为θ+φ的点.

参数s的闵氏旋转和参数t的闵氏旋转的复合是参数s+t的闵氏旋转.这在代数上等价于公式ch(s+t)=ch(s)ch(t)+sh(s)sh(t)和sh(s+t)=ch(s)sh(t)+sh(s)ch(t).读者可以利用双曲函数的定义与指数函数的性质直接证明.

一个一般的闵氏变换是O(1,1)中变换和一个平移变换的复合变换.它具有形式

(x,y)=(x′,y′)T+(x0,y0).

对于欧氏情形有以下简单的结论.

命题1E2中的任一向量a=(x,y)可以通过以原点为中心的欧氏旋转变换变成标准形式(k,0),k>0或者(0,0).

对于闵氏几何，事情会更复杂一些.

命题2M2中的任一向量a=(x,y)可以通过以原点为中心的闵氏旋转和关于x和y轴的反射变换变成四类标准形式(k,0),(0,k),k>0,(1,1),(0,0)之一.

证明任取一点，设其坐标为(x,y).若a=(0,0)，则它变为(0,0).若它在光锥上，且不是原点，则x2-y2=0，利用反射可以将它变为(x,x),x>0.再通过闵氏旋转可以变为

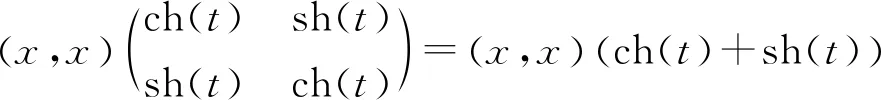
=(x,x)et

若x>0，通过选取适当的t可以使得(x,x)et=(1,1).

类似的若x2-y2=k2>0，则能够将(x,y)变为(k,0)；若x2-y2=k2<0，则(x,y)可以变为(0,k).读者可以自己去验证.

3 闵科夫斯基空间的直线和二次曲线的分类.

欧氏平面上的任意直线可以通过欧氏变换变成x轴.闵氏平面上的直线可以通过闵氏变换变成x轴、y轴或者直线y=x.出现这三种情形是因为直线的方向向量有类时、类空和类光三种情形.

我们也可以讨论闵氏空间中的二次曲线的分类，因为分类比较复杂，所以不再赘述.读者可参考文献[1]中欧氏情形的讨论，自己尝试去给出相应结果.