数学模型在购房贷款中的应用

广东省广州市第七中学 黄佳泰

贷款购房是人们生活中常见的消费贷款方式之一，寻求最优的贷款方案，为购房决策提供依据具有重要意义.目前，银行主要提供两种房贷还款方式：等额本金还款和等额本息还款.

等额本息还款，是指把按揭贷款的本金总额与利息总额相加，然后平均分摊到还款期限的每个月中，每个月按照相等（固定）的金额进行还款.

等额本金还款，是指把按揭贷款的本金总额平均分摊到每个月内，同时付清上一交易日至本次还款日之间的利息.这种还款方式相对等额本息还款而言，总的利息支出较低，但是前期支付的本金和利息较多，还款负担逐月递减.

一、提出问题

购房者李某向中国工商银行贷款100万元，贷款期限为20年或30年，2019年中国工商银行五年期以上银行贷款年利率为4.9%，规定按月还款.还款方式有两种，一是等额本息还款法，二是等额本金还款法.购房者可根据自身情况选择其中一种还款方式.那么购房者李某应选择哪种贷款期限，哪种还款方式所支付的还款总额更划算？

二、明确变量参数，模型假设

设银行贷款a万元，贷款期限为n个月，贷款月利率为r，每个月还款为x万元，第n个月（0≤n）尚欠银行本金为an，第n个月还款额为bn.采用等额本息还款方式所需支付的还款总额为Sa，采用等额本金还款方式所需支付的还款总额为Sb.

三、归纳变量关系，建立模型

（1）若采用等额本息还款方式，则有：

第1个月还款后，所欠银行的本金是a1=a-（x-a·r）=a（1+r）-x；

第3个月还款后，所欠银行的本金是a3=a2（1+r）-x=

……

由数学归纳法和等比数列求和公式可得，第n个月还款后，所欠银行的本金为an=an-1（1+r）-x=a（1+r）n-

所以当贷款还清时，an=0，由此可得：

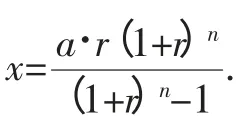
因此，采取等额本息还款法经n个月还清贷款时，总还款额Sa为：

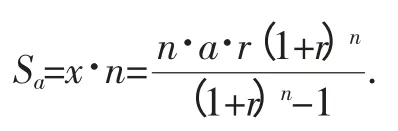
（2）若采用等额本金还款方式，则有：

……，

由数学归纳法可见，每月归还的还款额构成等差数列，且公差为

根据等差求和公式可得，第n个月后共归还银行的还款额Sb为：

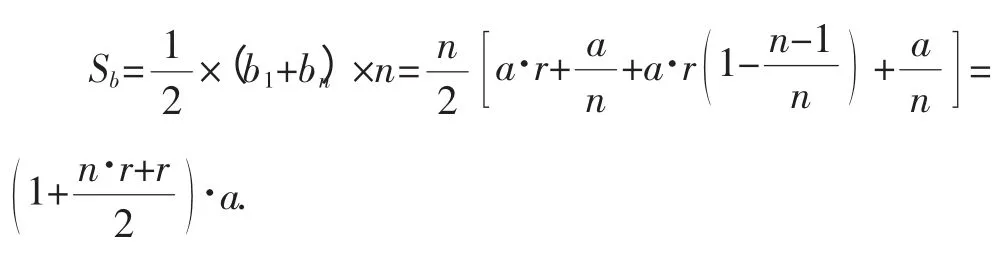
四、问题求解

由年利率4.9%可得，月利率为0.40833333333%.下面分别把r=0.40833333333%，a=100万元代入上面的数学模型则有：

当n=240时，

当n=360时，

经过以上计算可知，在不考虑其他因素的情况下，购房者李某选择贷款期限为20年，采取等额本金还款方式的贷款策略最划算，仅需要149.204167万元即可.F