考虑表面粗糙度和热效应的线接触非牛顿混合润滑分析*

(青岛理工大学机械与汽车工程学院 山东青岛 266520)

在实际工程中，大部分线接触副都处于混合润滑状态。对于混合润滑的研究，JOHNSON等[1]率先提出了载荷分享机制，即总载荷由油膜与粗糙峰共同承载。PATIR和CHENG[2]考虑了表面粗糙度的影响，并使用流量因子来修正Reynolds方程，得到平均Reynolds方程。MASJEDI和KHONSARI[3]结合文献[2]的研究成果，并基于粗糙峰接触模型建立了线接触混合润滑模型，系统地研究了工况条件、粗糙峰参数、材料参数对油膜厚度、油膜压力以及载荷比的影响，并通过大量的数值模拟，拟合出合适的中心膜厚、最小膜厚以及载荷比公式。刘乐民等[4]基于Patir-Cheng平均流量理论研究了表面波纹度、表面粗糙度以及润滑液黏度系数等因素对于轧制界面压力和摩擦力的影响。雷渡民和王素华[5]研究了混合润滑状态下表面织构参数对滑动轴承承载能力和摩擦因数的影响。但文献[4-5]都假定流体是不可压缩的，忽略了流体的可压缩性质。王志坚等[6]研究了表面粗糙度和润滑油性质对有限长线接触副润滑性能的影响，但其没有涉及非牛顿流体的讨论。

在混合润滑状态下必须考虑粗糙峰接触的影响。GREENWOOD和WILLIAMSON[7]提出了GW模型，模拟了光滑表面与粗糙表面的接触。GREENWOOD和TRIPP[8]拓展了GW模型，考虑了2个粗糙表面的接触，表明对于2个粗糙表面的接触GW模型是有效的。但是，GW模型只能用于粗糙峰的弹性变形，在发生塑性变形的情况下，GW模型预测的粗糙峰接触压力过高。考虑粗糙峰的弹性变形与塑性变形已成为摩擦学关注的重点。CHANG等[9]提出了CEB模型，将粗糙峰变形分为弹性变形与全塑性变形，但并没有考虑弹性变形到全塑性变形的过渡区。ZHAO等[10]开发了ZMC模型，考虑了弹性变形、弹塑性变形和完全塑性变形。ZMC模型的准确性要高于GW模型与CEB模型。

综上所述，基于平均流量模型，考虑表面粗糙度及热效应对非牛顿混合润滑影响的研究尚不多见。本文作者拟基于平均流量模型，建立线接触非牛顿混合润滑模型来研究表面粗糙度和热效应的影响。

1 数学模型

采用Eyring流变模型，等效黏度方程为

(1)

式中：η*为等效黏度；τ0表示Eyring流体的特征剪应力；τ表示剪应力；η表示非牛顿流体的表观黏度。

在混合润滑中，总负载是由油膜与粗糙峰共同承担的，所以在任何点的总压力p始终是油膜压力ph与粗糙峰压力pa之和：

p=ph+pa

(2)

为了计算油膜压力、油膜厚度和油膜温度，需要将非牛顿流体的平均Reynolds方程、膜厚方程、载荷平衡方程以及能量方程共同求解；粗糙峰接触压力由粗糙峰接触模型求解。因此，将数学模型分为2个模块：流体模块和粗糙峰接触模块。

1.1 流体模块

图1给出了粗糙表面接触时的油膜厚度模型，图中，ua、ub分别表示固体a、b的运动速度，且ua>ub，ht表示实际油膜厚度，h表示由2个粗糙表面中线构成的名义膜厚。

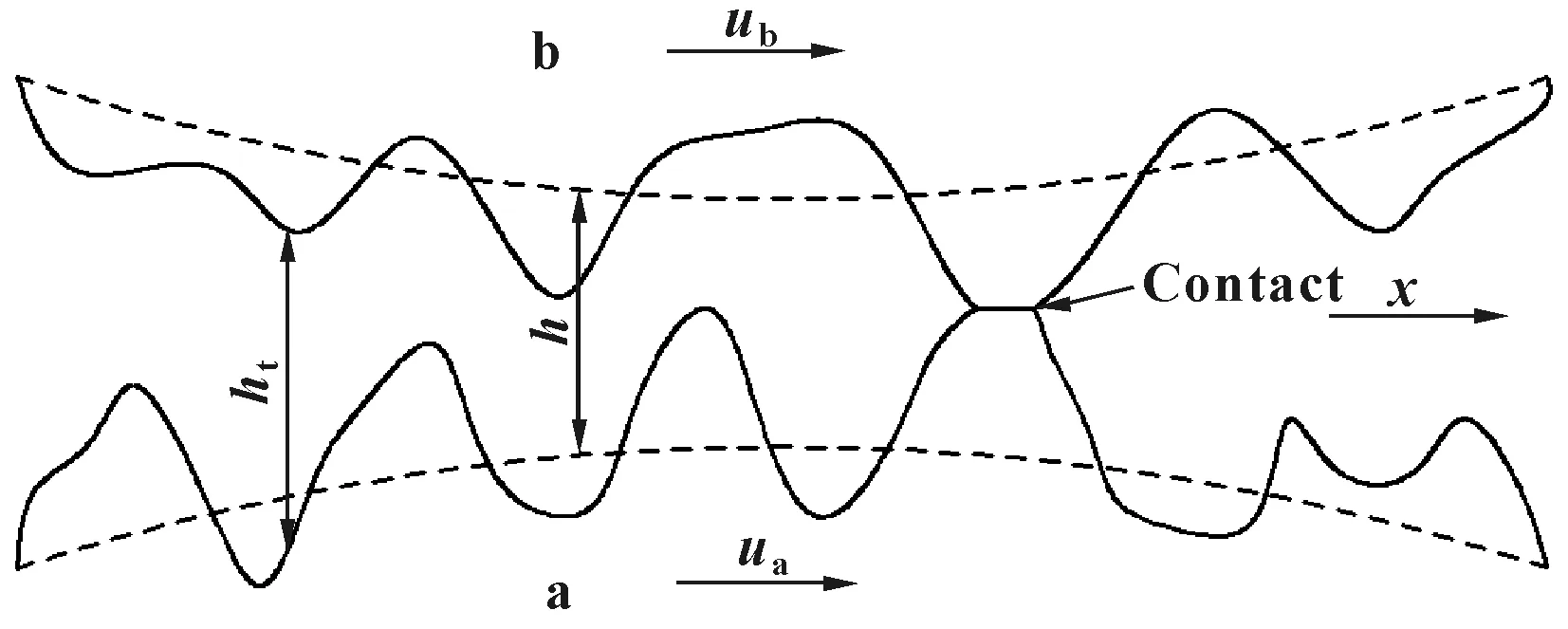
图1 粗糙表面接触时的油膜厚度Fig 1 The oil film thickness on rough surface contact

由PATIR和CHENG[2]平均流量模型，并假设固体a、b表面粗糙峰的分布一致，推导出广义平均Reynolds方程：

(3)

式中：φx表示压力流量因子;ue表示卷吸速度，ue=(ua+ub)/2；hT表示ht的平均值，称为运动表面的平均间隙；ρ表示润滑油的密度。

对于粗糙度是高斯分布的各向同性表面，PATIR和CHENG[2]推导了φx的表达式。

(4)

hT的表达式[11]可写为

(5)

广义平均Reynolds方程的边界条件为

(6)

式中：xin、xout表示计算域的边界。

式(1)中非牛顿表观黏度η和式(3)中密度ρ分别可通过Roelands黏压-黏温关系式[12]和Dowson-Higginson密压-密温关系式[13]求解。

η=η0exp{A1[-1+(1+A2ph)Z0(A3T-A4)-S0]}

(7)

Z0=α/[5.1×10-9(lnη0+9.67)]

S0=βT(T0-138)/(lnη0+9.67)

A1=lnη0+9.67，A2=5.1×10-9

A3=1/(T0-138)，A4=138/(T0-138)

式中：η0表示环境黏度；T表示油膜温度；α表示润滑油的黏压系数；βT表示润滑油的黏温系数；T0表示环境温度。

(8)

式中：ρ0为环境密度；ε=0.000 65。

式(3)中的油膜名义厚度h由下式求得：

(9)

式中：h00表示两表面的变形量。

需要注意的是，计算两表面的变形量所使用的压力是总压力p。

总载荷是由油膜与粗糙峰共同承载的，故载荷平衡方程的表达式为

(10)

载荷比的表达式为

(11)

式(7)和式(8)中的温度T由油膜的能量方程式(12)求得。

(12)

式中：c、k分别表示油膜比热容和热传导系数；u表示油膜流速；Qa为由粗糙峰引起的单位体积热量。

(13)

式中：us=|ua-ub|表示两粗糙峰接触时的滑动速度；fa表示粗糙峰接触时的摩擦因数。

固体a、b的能量方程：

(14)

式中：ca、cb分别表示固体a、b的比热容；ρa、ρb分别表示固体a、b的密度；ka、kb分别表示固体a、b的热传导系数。

固体a、b表面满足如下的热流量连续条件：

(15)

1.2 粗糙峰接触模块

为考虑粗糙峰的弹性变形、弹塑性变形以及完全塑性变形，采用ZHAO等[10]建立的粗糙峰接触模型(ZMC)，粗糙峰接触应力由下式求解：

(16)

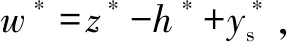
根据McCool的计算[14]，σs和ys的计算式为

(17)

1.3 接触副摩擦因数的计算

在混合润滑中，载荷由油膜与粗糙峰共同承载，因此，接触副的摩擦力由2部分构成：

F=Fh+Fa

(18)

式中：Fh表示油膜内剪应力产生的摩擦力;Fa表示粗糙峰接触产生的摩擦力。

(19)

(20)

因此，计算域内的平均摩擦因数的计算式为

fc=F/w′

(21)

2 数值方法

油膜压力求解采用多重网格法，膜厚方程中弹性变形采用多重网格积分法，温度场采用逐列扫描法求解。采用6层网格，最高层网格节点数为960个节点，计算域的起点坐标与终点坐标分别为Xin=-4.6，Xout=2.4。当压力相对误差与温度相对误差小于1×10-4，载荷相对误差小于1×10-3时达到收敛精度，跳出循环，计算结束。

3 计算结果及分析

公共输入的参数：ue=0.57 m/s ，pH=0.9 GPa，滑滚比ζ=0.5，β=σ/0.01，T0=303 K(30 ℃)，hd=0.01E′，fa=0.15。固体a、b的参数见表1，润滑油的参数见表2。

表1 接触固体的参数

表2 润滑油的参数

3.1 表面粗糙度对热效应膜厚、膜厚比、载荷比及平均摩擦因数的影响

图2(a)、(b)分别给出了等温及热条件下的中心膜厚hcen、最小膜厚hmin与膜厚比λ(λ=hmin/σ)随表面粗糙度σ的变化。由图2(a)可以看出，在等温条件下，由于“泵效应”的影响，中心膜厚与最小膜厚随着表面粗糙度的增大而增大。在热条件下，随着表面粗糙度的增大，中心膜厚与最小膜厚先增大后减小，原因在于表面粗糙度较小时热效应对膜厚的影响较小，表面粗糙度对膜厚的影响占据主导地位，所以膜厚随表面粗糙度的增大而增大；随着表面粗糙度增大，热效应对膜厚的影响逐渐变大，当热效应占主导地位时，膜厚减小，使得等温与热条件下膜厚的差值随着粗糙度的增大而增大。

由图2(b)可知，等温及热条件下的膜厚比随着表面粗糙度的增大而减小。在等温条件下，虽然最小膜厚逐渐增大，但是其膜厚比逐渐减小，原因在于表面粗糙度增大的幅度大于最小膜厚增大的幅度。虽然等温条件下最小膜厚与热条件下最小膜厚的差值随着表面粗糙度的增大而增大，但是2种情况下膜厚比的差值变化不大。主要原因是，表面粗糙度增大的幅度大于最小膜厚增大的幅度。

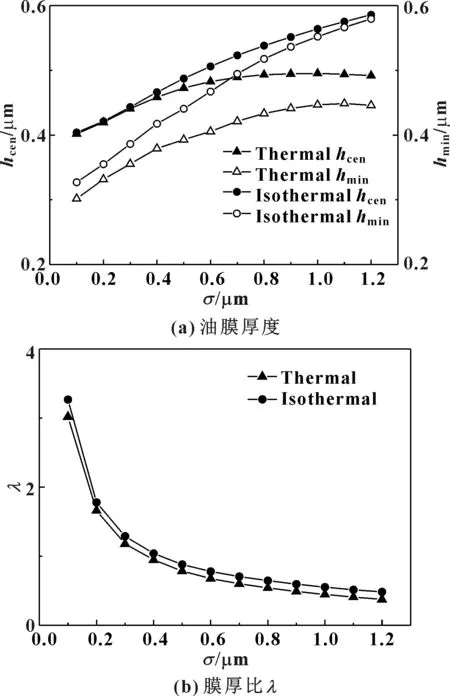
图2 油膜厚度与膜厚比λ随表面粗糙度σ的变化趋势Fig 2 Variation of film thickness and film thickness ratio with surface roughness σ(a) film thickness;(b) film thickness ratio λ

图3给出的是在等温及热条件下，载荷比La随表面粗糙度的变化。可知，载荷比随着表面粗糙度的增大而增大，主要由于，虽然在等温条件下，膜厚随表面粗糙度增加而增大(如图2(a)所示)，但是表面粗糙度增大的幅度比膜厚增大的幅度大，即膜厚相对于粗糙度减小了，导致更多的粗糙峰接触，进而使粗糙峰承受的载荷变大。尤其是在热条件下，膜厚随粗糙度的增加先增大再减小，相对于表面粗糙度，油膜变得更薄。因此，等温与热条件下载荷比的差值逐渐增大。

图3 载荷比La随表面粗糙度的变化趋势Fig 3 Variation of load ratio with surface roughness σ

图4给出的是在等温及热条件下平均摩擦因数fc随表面粗糙度σ的变化。可知，平均摩擦因数随表面粗糙度的增大而增大。等温条件下，平均摩擦因数要比热条件下大，但是其差值逐渐减小。原因在于，在同一表面粗糙度下，受热效应的影响，润滑油的黏度降低，进而使油膜内部的摩擦力减小，使得热条件下的平均摩擦因数比等温条件下小。

图4 平均摩擦因数fc随表面粗糙度σ的变化趋势Fig 4 Variation of average friction coefficient fc with surface roughness σ

随着表面粗糙度的增加，载荷比增大(如图3所示)，粗糙峰之间的摩擦力增大，粗糙峰摩擦力逐渐占据主导位置。因此，与等温条件相比，热条件下的平均摩擦因数增大的趋势更明显，使得等温与热条件下摩擦因数的差值逐渐减小。

3.2 表面粗糙度对油膜温度的影响

图5所示为压力随表面粗糙度的变化，包括总压力p、油膜压力ph、固体接触压力pa的变化趋势。可知，随着表面粗糙度的增大，总压力的承载区域增大，油膜压力降低、承载区域减小，固体接触压力上升、承载区域增大。

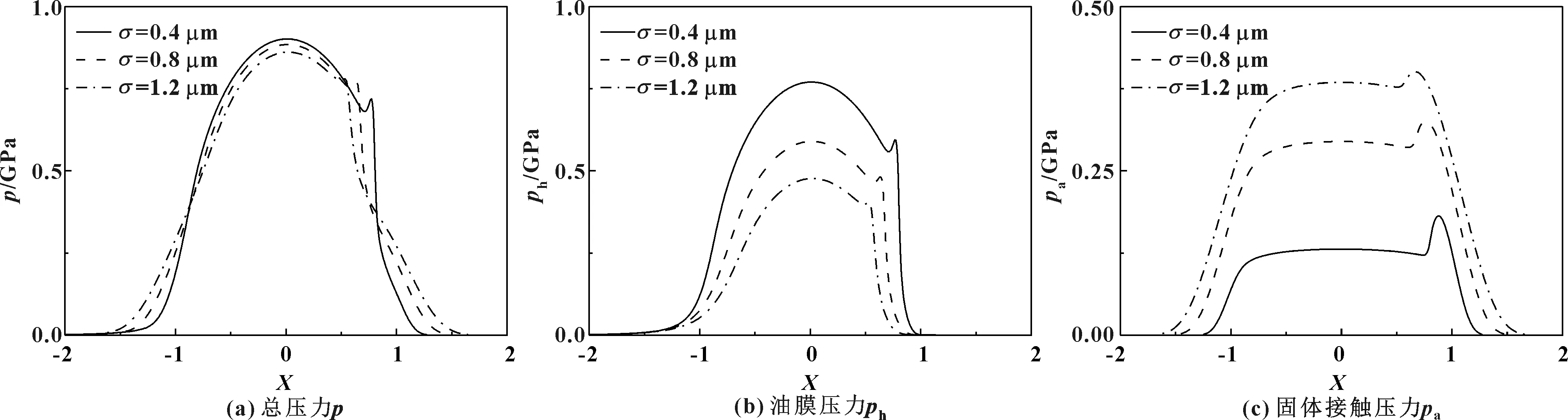
图5 压力随表面粗糙度σ的变化趋势Fig 5 Variation of pressure with surface roughness σ (a) total pressure p;(b) hydrodynamic pressure ph;(c) asperity pressure

图6所示为温度随表面粗糙度的变化，包括固体a表面温度ta、中层油膜温度t、固体b表面温度tb的变化趋势。可知，随着表面粗糙度的增大，油膜温度逐渐升高，尤其是入口区与出口区的温升最为明显。主要由于，随着表面粗糙度的增大，固体接触压力上升且承载区域增大(如图5(c)所示)，这反映了更多的粗糙峰相互接触，粗糙峰摩擦产生的热量要比油膜内部产生的剪切热大，且由于固体接触压力的承载区域增大，油膜压力的承载区域减小，因此，温升在入口区与出口区最为明显。

图6 温度随表面粗糙度σ的变化趋势Fig 6 Variation of temperature with surface roughness σ (a) surface temperature of solid a;(b) mid-layer film temperature t; (c) surface temperature of solid b

4 结论

(1)考虑热效应时，随着表面粗糙度的增大，膜厚先增大后减小，载荷比及平均摩擦因数增大，膜厚比减小。

(2)考虑热效应时，随着表面粗糙度的增大，膜厚变化的趋势与等温条件下差异较大，膜厚比与平均摩擦因数较等温解小，而载荷比较等温解大，这表明混合润滑条件下热效应的影响不可忽略。

(3)随着表面粗糙度的增大，油膜温度逐渐升高，尤其是出口区与入口区的温升最为显著。