旋转圆筒泄漏流模型研究*

赵国昌1 王 泉 宋丽萍1 邢仕廷

(1.中国民航大学适航学院 天津 300300；2.中国民航大学中欧航空工程师学院 天津 300300)

叶尖泄漏流动是叶轮机械中普遍存在的现象，由于气流流过叶背与叶盆的速度不同，导致吸力面与压力面间存在周向压差，引起泄漏流动。叶尖间隙过大将引起较大的泄漏流量，从而降低叶轮机工作效率，增加使用成本；叶尖间隙过小，将导致叶片在离心力的作用下与机匣发生碰撞或摩擦，危害叶轮机运行安全。研究表明,叶尖间隙为叶片高度的1%～3%较好[1-4]。为获得叶尖泄漏流动规律，本文作者对周向压差作用下同轴旋转圆筒间泄漏流进行研究。

同轴旋转圆筒间流动即Taylor-Couette问题的研究结果，广泛应用于润滑、密封等领域[5-8]。在初始的Taylor-Couette问题上引入新的变量，如加入周向压力梯度探究其对圆筒间流动的影响，具有重要的工程应用价值。考虑周向压力梯度的影响最早由Dean提出，因此又被称为Taylor-Dean问题[9]，目前对此方面的研究主要集中在对圆筒间流动稳定性分析上[10-14]，通过求解其临界泰勒数，描述流动从层流到湍流的转捩过程，而对圆筒间隙内流体流量影响规律的研究相对较少。

本文作者采用二维周向压力梯度下同轴旋转圆筒模型分析转速比、半径比等因素对叶尖泄漏流量的影响。

1 物理模型

周向压力梯度下旋转圆筒二维模型如图1所示，模型包含旋转速度不同的内外同轴圆弧，圆弧对应的圆心角为θ，其中内弧半径为R1，转速为Ω1；外弧半径为R2，转速为Ω2；压力梯度沿周向分布均匀，进口压力为p1，出口压力为p2。求解同轴圆弧间流体速度分布，获得通过旋转圆筒间不可压缩牛顿流体的体积流量，为泄漏流动研究提供理论基础。

图1 二维周向压力梯度下旋转圆筒模型Fig 1 Two-dimensional circumferential pressure gradient rotating cylinder model

根据经典黏性流体力学理论[15-17]，用连续方程、径向动量和周向动量方程描述该模型的控制方程组。

(1)连续方程

(1)

(2)径向动量方程

(2)

(3)周向动量方程

(3)

由于圆筒的半径很小，径向速度可以忽略，且二维模型不考虑轴向速度，则方程(1)可简化为

(4)

由于径向速度为0且流动定常，轴向速度关于转角的偏导数为0且不考虑体积力，因此径向动量方程可简化为

(5)

假设周向动量方程的径向速度为0且流动定常，轴向速度为0、轴向速度关于转角的偏导数也为0且不考虑体积力，因此

(6)

2 数学求解

相比于周向压力梯度，径向压力梯度很小，可近似为0，文中只考虑周向压力梯度对流动的影响，方程(6)可以通过无周向压力梯度的同轴旋转圆筒间的定常流动和有周向压力梯度下固定圆筒的Poiseuille流动2个解相叠加求得。

2.1 不考虑周向压力梯度的同轴旋转圆筒间的定常流动

不考虑周向压力梯度的同轴旋转圆筒间定常流动解只需考虑内外圆筒旋转对流动的影响，式(6)简化为

(7)

该方程的解

(8)

为了求出常数A和B，引入方程边界条件[18]

r=R1uθ(r=R1)=Ω1R1

(9)

r=R2uθ(r=R2)=Ω2R2

(10)

求解得到

(11)

(12)

其中，

2.2 考虑周向压力梯度的固定圆筒间的流动

描述固定圆筒间有周向压力梯度的流体流动的控制方程由式(6)表达，为便于求解，将式(6)改写为

(13)

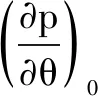
(14)

其中C、D为常数，引入边界条件[19]

r=R1，uθ(r=R1)=0

(15)

r=R2，uθ(r=R2)=0

(16)

得到

(17)

(18)

2.3 考虑周向压力梯度旋转圆筒间的定常流动

将2.1节中无周向压力梯度的同轴旋转圆筒间的定常流动解和2.2节中有周向压力梯度下固定圆筒的Poiseuille流动解相叠加，得出周向压力梯度下同轴旋转圆筒间定常流动周向速度解析解

(19)

2.4 泄漏流体积流量的求解

利用式(19)求得的二维周向压力梯度下旋转圆筒间周向速度解析解，通过积分得到旋转圆筒间泄漏体积流量表达式

(20)

考虑沿轴向存在单位长度，因此

(21)

代入周向速度表达式式(19)可得

(22)

代入常数A、B、C、D可得

(23)

(24)

其中

(25)

(26)

3 结果和讨论

3.1 η和ζ对Q1，Q2的影响

为便于讨论，定义量纲一体积流量

(27)

(28)

联立式(25)、(27)得到Q1与量纲一化数η和ζ的关系式。由内外圆筒转动引起的泄漏流Q1随半径比和转速比的变化趋势如图2和图3所示。

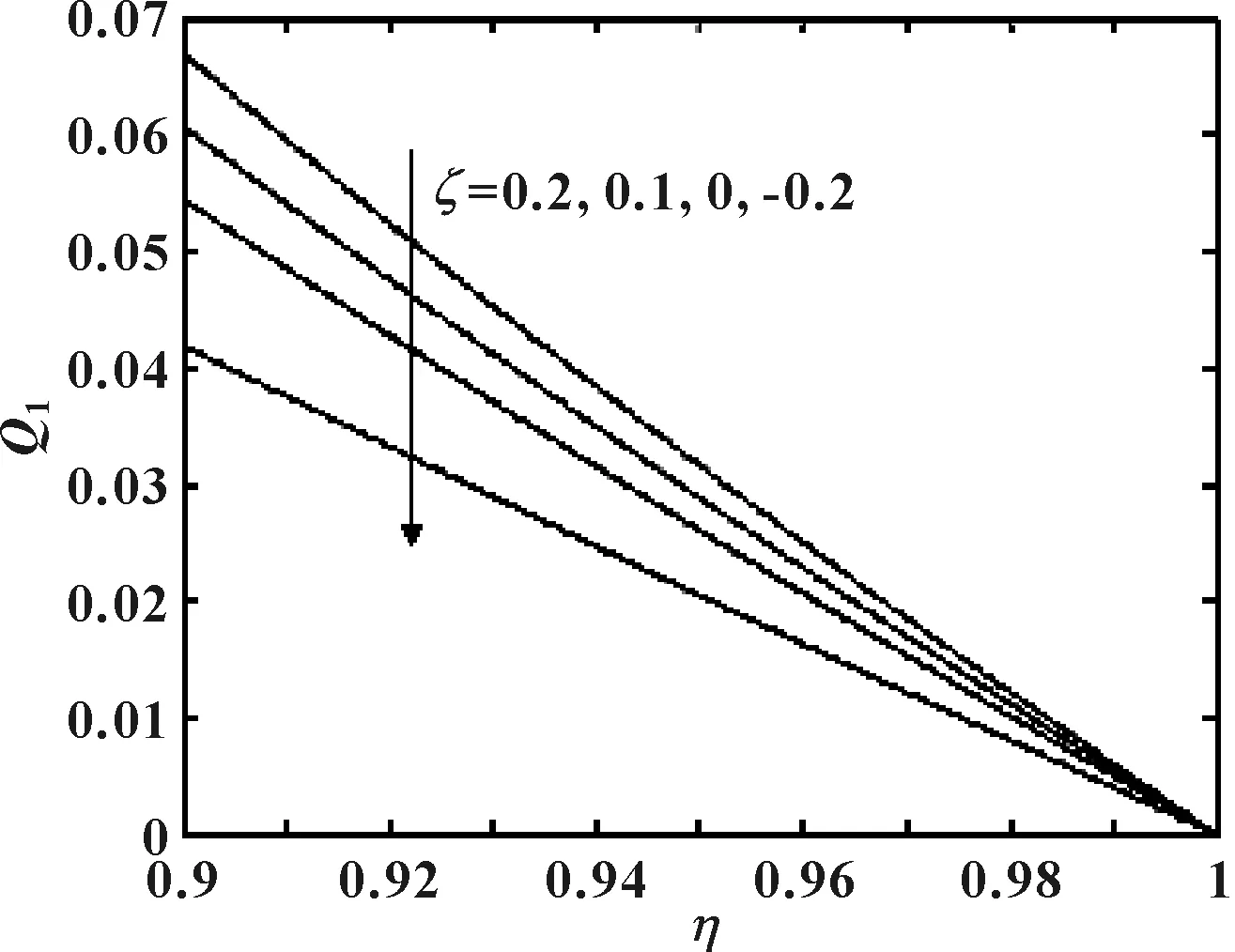
图2 η对Q1的影响Fig 2 The influence of η on Q1

由图2可知，半径比η一定时，由内外圆筒转动引起的泄漏体积流量Q1随着转速比ζ的增加而增加；当半径比η由小变大时，随转速比ζ增大，泄漏体积流量的增加率变小。

图3 ζ对Q1的影响Fig 3 The influence of ζ on Q1

由图3可知，转速比ζ一定时，由内外圆筒转动引起的泄漏体积流量Q1随着半径比η的增加而减小；当半径比η为1时，泄漏量为0；当半径比一定时，转速比ζ越大泄漏量越大，两圆筒反向转动(ζ<0)可降低泄漏流量。

联立式(26)、(28)得到Q2与量纲一化数η的关系式。因此处没有旋转，由周向压力梯度引起的泄漏量Q2只需考虑半径比的影响，图4所示为η对Q2的影响曲线。

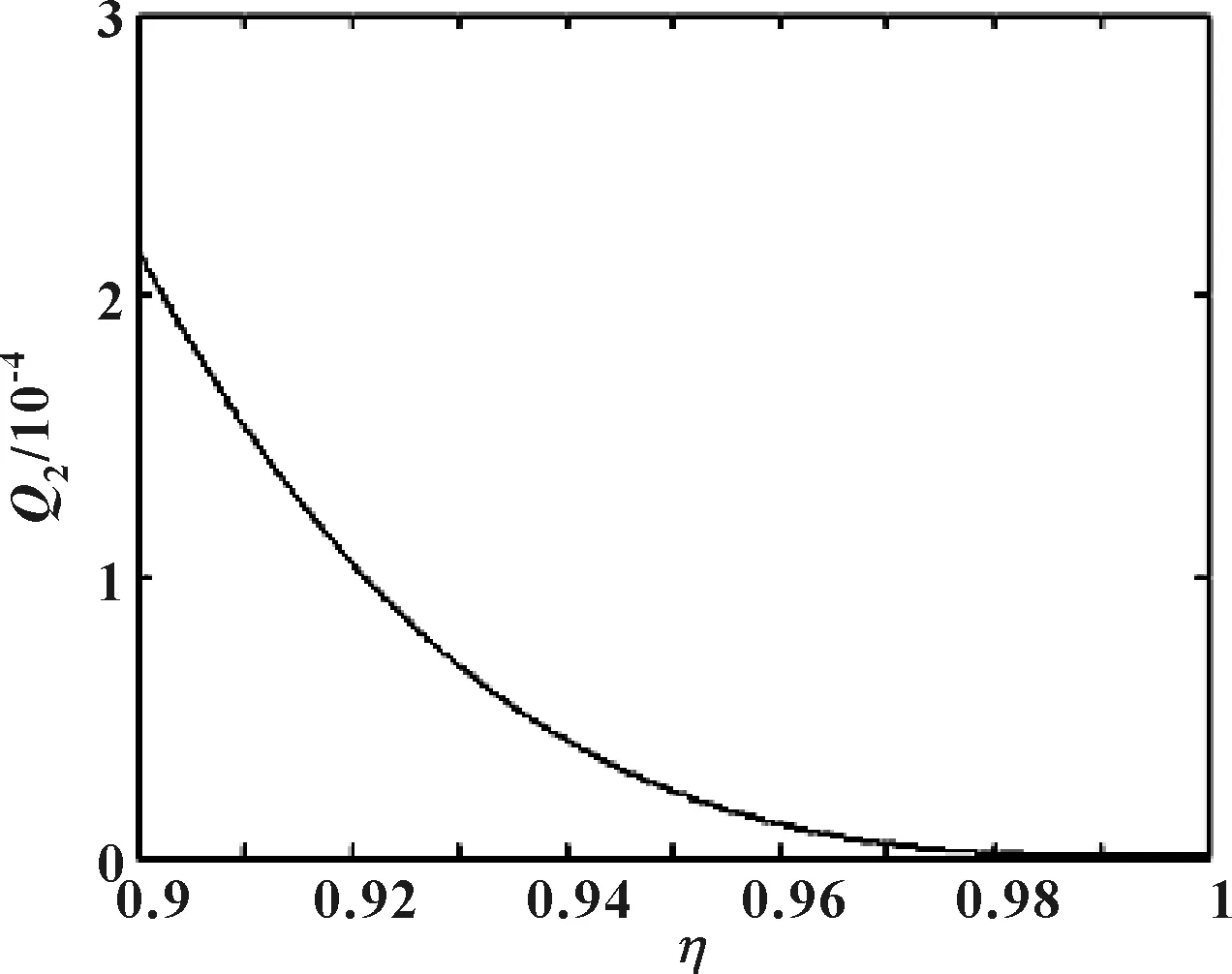
图4 η对Q2的影响Fig 4 The influence of η on Q2

由图4可知，由周向压力梯度引起的泄漏体积流量Q2随半径比η的增加而减少，当η趋于1时，Q2趋于0；由周向压力梯度引起的量纲一泄漏量Q2比由圆筒转动引起的量纲一泄漏量Q1小2个数量级。

3.2 介质对泄漏流的影响

以空气、水和甘油3种介质为例研究总泄漏量随半径比的变化，为便于分析对式(24)—(28)进行简化。定义

(29)

由式(24)、(27)—(29)可得

(30)

定义

(31)

则

(32)

在给定的压差、转角、内圆筒转速和转速比等参数下，研究了半径比等因素对泄漏流的影响。因较大压差会影响流态，文中给定压差为100 Pa，转角θ=π/2，假设流动为充分发展流动，周向压力沿圆周方向均匀下降，压力梯度为63.66 Pa/rad，取内圆筒转速为1 000 r/min，转速比ζ=0.1。20 ℃时空气、水和甘油3种介质的动力黏度及Ωp/Ω1值如表1所示。

表1 20 ℃时介质的黏度及Ωp/Ω1值

由图2和图4已知，Q1约为Q2的100倍，结合表1中的Ωp/Ω1数值，20 ℃时空气的Q2·Ωp/Ω1值远大于Q1；水的Q2·Ωp/Ω1值与Q1相当；甘油的Q2·Ωp/Ω1值远小于Q1。3种介质的量纲一泄漏总体积流量如图5—7所示。

图5 η对Q的影响(空气，ζ=0.1)Fig 5 The influence of η on Q (air,ζ=0.1)

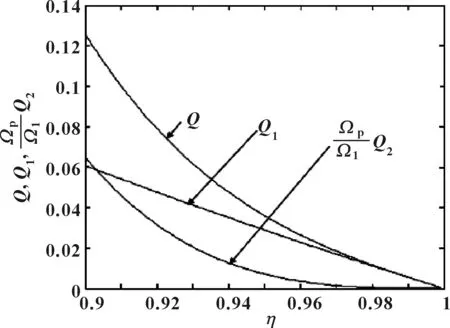
图6 η对Q的影响(水，ζ=0.1)Fig 6 The influence of η on Q (water,ζ=0.1)

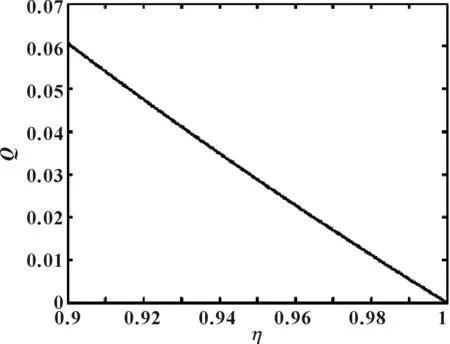
图7 η对Q的影响(甘油，ζ=0.1)Fig 7 The influence of η on Q (glycerin,ζ=0.1)

由图5可知，随着半径比η的增加，总泄漏流体积流量Q减少，由于影响泄漏流量的主要因素为周向压差，图5的变化趋势与图4一致。由图6可知，随着半径比η的增加，Q1和Q1·Ωp/Ω1减少，因此总体积流量Q减少。由图7可知，随着半径比η的增加，总泄漏流体积流量Q减少，由于影响泄漏流量的主要因素为圆筒转动，图7的变化趋势与图2一致。

3.3 温度对泄漏流的影响

在给定的压差、转角、内圆筒转速和转速比等参数下，研究了温度变化对泄漏流量的影响。由式(23)可知，温度主要通过影响介质的动力黏性从而影响泄漏流的体积流量。对于甘油，其泄漏流量主要由Q1决定，因此温度变化对其总泄漏流量Q影响很小，可以忽略。空气和水在温度t变化范围内的动力黏度μ及Ωp/Ω1值如表2所示。当ζ=0.1时，介质为空气，η对Q影响如图8所示；介质为水，η对Q影响如图9所示。

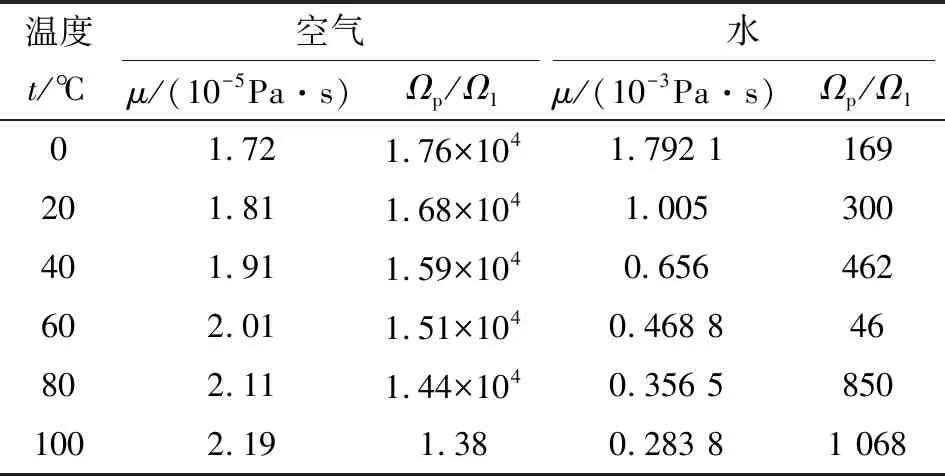
表2 温度对动力黏度和Ωp/Ω1的影响

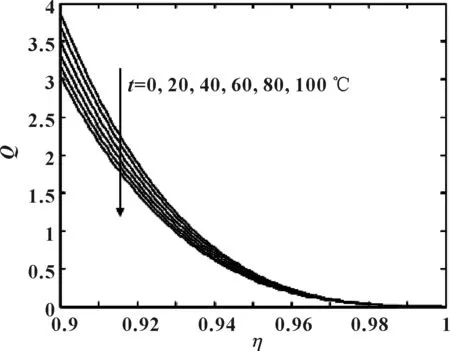
图8 η对Q的影响(空气，ζ=0.1)Fig 8 The influence of η on Q (air,ζ=0.1)

图9 η对Q的影响(水，ζ=0.1)Fig 9 The influence of η on Q (water,ζ=0.1)

由图8可知，随着温度升高空气的黏性增加，泄漏流流量减小。与图8相对照，由图9可知温度升高水的黏性降低，泄漏流流量增加。由图8和图9可知，随着半径比的增加，总泄漏量逐渐减少最终趋于0。

4 结论

(1)由转动引起的泄漏流体积流量随着转速比的增加而增加，随着半径比的增加而减少，同向转动时的泄漏流流量大于反方向转动时的泄漏流流量；由周向压力梯度引起的泄漏流体积流量随着半径比的增加而减少。

(2)动力黏度较小的介质如空气，影响其泄漏流体积流量的主要因素为周向压力梯度，动力黏度较大的介质如甘油，影响其泄漏流体积流量的主要因素为圆筒转动，动力黏度介于两者之间的介质如水，需要考虑两者的共同作用。

(3)介质温度影响介质的动力黏度从而影响泄漏流流量。空气温度增加其动力黏度增大，泄漏流流量减小；水温度增加其动力黏度减小，泄漏流流量增加。