基于流体压力渗透法的齿形滑环组合密封有限元分析*

(西南石油大学机电工程学院 四川成都 610500)

滑环组合密封圈在高压动密封领域有广泛的应用，比如高压航空作动器，深海高压环境下装备的组合密封以及石油天然气装备与井下工具等[1-4]。这种组合密封圈将橡胶O形圈和PTFE滑环配合使用，充分发挥了O形圈在流体压力下的自密封效果和PTFE材料与金属间摩擦因数较低的优势，较好地实现了高压条件下的动密封[5]。张教超等[6]对齿形滑环组合密封进行了分析，分析了压缩量、介质压力及齿形滑环结构对组合密封的接触应力及变形的影响。陈家旺等[7]对组合密封件进行了有限元仿真，并计算了摩擦扭矩。刘清友[8]等对C 形滑环式组合密封的密封性能进行了有限元分析。谭晶等人[9-10]分别对格莱圈和斯特圈进行仿真分析。然而，学者们在使用有限元软件分析组合密封圈性能时，在模拟装配阶段通常采用的是位移加载的方式来实现，然而这种加载方式会导致齿形滑环最先发生变形，进而导致O形圈变形，且这种加载方式会导致橡胶元件的接触次序与实际不符，因而计算得到的接触压力往往不准确；在模拟流体压力对密封圈的作用时，通常采用指定边界法，指定边界法需要研究者估计接触与分离的临界点然后直接给定。这样往往得到不到与实际相符合的结果。

为了得到更精确的理论结果，本文作者利用ABAQUS软件的自动收缩配合方式来模拟密封圈的装配安装过程；再采用流体压力渗透载荷的加载方式来模拟流体压力对密封圈的作用。结合这2种方法对该齿形滑环组合密封圈进行数值模拟，研究了组合密封中O形圈压缩率和工作介质压力对齿形滑环组合密封圈密封性能的影响，计算结果可以为旋转动密封的理论计算提供相关参数，为齿形滑环组合密封圈的实际应用提供相关依据。

1 齿形滑环组合密封圈有限元分析

1.1 计算模型

研究所用的滑环式组合密封圈型号为TB3-I 50×5.3[11]。滑环的材料是增强聚四氟乙烯(PTFE)，具有很低的摩擦因数；O形密封圈的材料为丁腈橡胶(NBR)，截面直径为5.3 mm。滑环式组合密封的二维轴对称模型如图1所示。

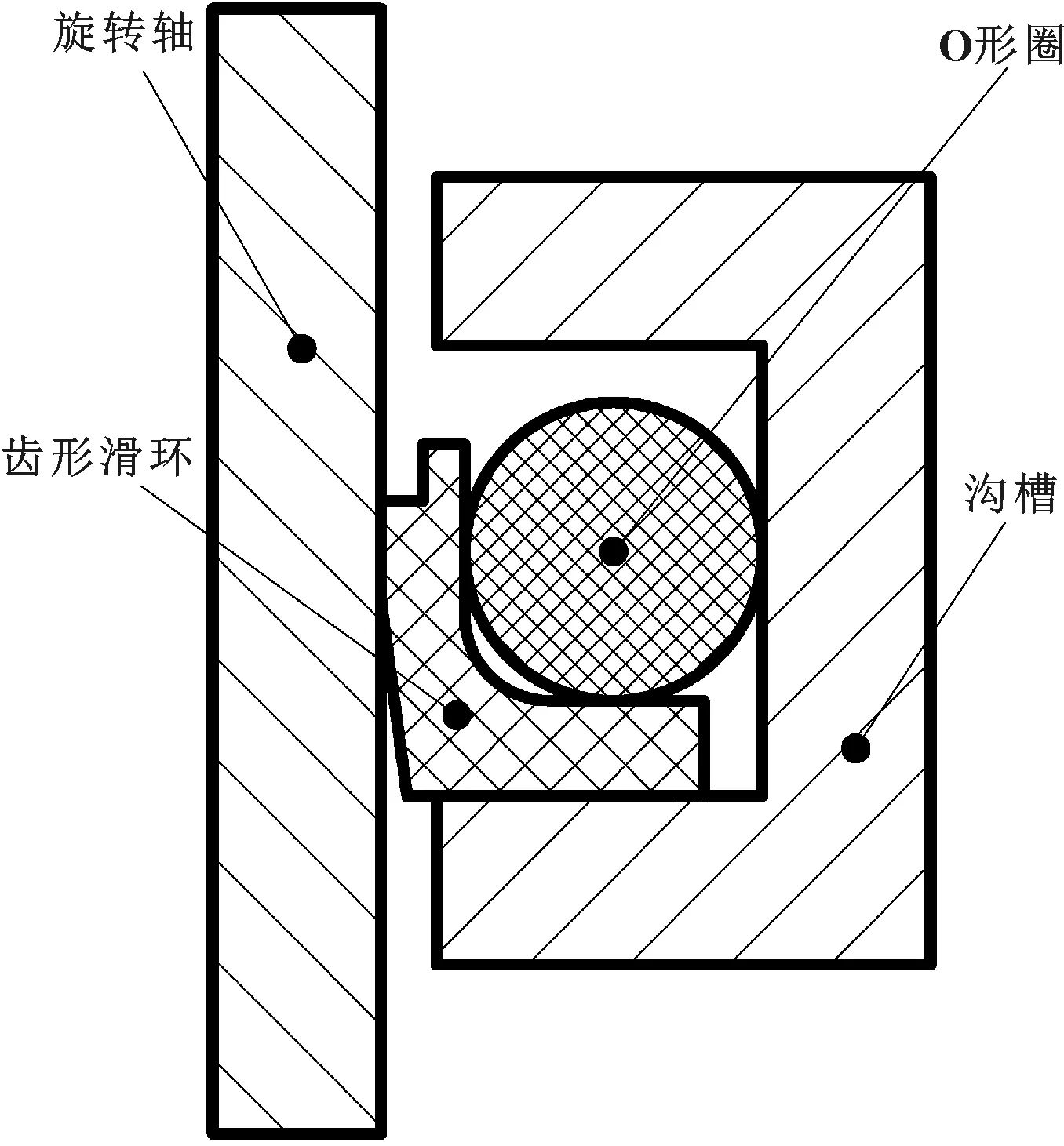
图1 二维轴对称模型Fig 1 2D axisymmetric model

1.2 有限元模型

橡胶密封件的密封计算是个非线性过程，非线性的来源包括几何非线性、材料非线性和边界非线性等[3]，因此很难对其进行精确的理论研究，因此，文中有限元分析基于三点假设：

(1)橡胶材料各向同性且完全弹性;

(2)忽略橡胶材料的应力松弛特性和蠕变特性;

(3)忽略温度和时间对橡胶材料性能的影响。

橡胶材料的本构模型选择Mooney-Rivlin模型[14]，其应变能密度函数为

(1)

式中：Ii(i=1,2,3)为i方向应变不变量；C10和C01为材料常数；kv为体积弹性模量。

其中，NBR橡胶的材料常数可以根据文献[6]得到，取值分别为C10=1.87 MPa，C01=0.47 MPa。此外，橡胶属于不可压缩的超弹性体，因此可令I3=1，则式(1)可以简化为

W=C10(I1-3)+C01(I2-3)

(2)

其应力应变的关系为

(3)

由于PTFE相对于NBR较硬，在应变小于50%时可以近似看作线弹性[12]，材料的弹性模量为200 MPa，泊松比为0.45。O形圈单元类型选用CAX4RH，齿形滑环单元类型选用CAX4R。对组合密封圈总共划分2 383个单元，各个接触对均采用罚函数法。O形圈与沟槽间摩擦因数定义为0.7，齿形滑环与旋转轴间摩擦因数定义为0.1，O形圈与齿形滑环间摩擦因数取0.6，齿形滑环与沟槽间摩擦因数取0.15[13]。

1.3 过盈装配仿真

图2(a)所示为采用位移约束模拟密封圈的过盈装配有限元模型，沟槽固定不动。根据密封圈样本手册[11]，旋转轴参考点向上移动0.795 mm。图2(b)所示为采用ABAQUS中自动收缩方式模拟过盈装配有限元模型，分别给旋转轴和沟槽指定参考点，将2个参考点固定不动，建模时，O形圈与沟槽相交部分的径向距离为0.795 mm，即为O形圈的压缩量为15%。

由密封圈样本手册可知，当旋转轴直径小于125 mm时采用开式沟槽[11]。实际装配过程为：先将齿形滑环与O形圈组合安装在旋转轴上，然后整体装入开式沟槽里，因此开式沟槽将最先与O形圈接触，O形圈的变形进一步导致齿形滑环与旋转轴之间产生接触压力。文中采用自动收缩配合方式能够较好地模拟实际的装配过程，图3(a)所示为自动收缩配合方式的计算结果，最大Mises应力为7.15 MPa。

图3(b)所示为位移约束模式的计算结果，可以看出在唇口附近产生了较大的Mises应力。可见，位移加载方式导致齿形滑环产生局部应力集中。

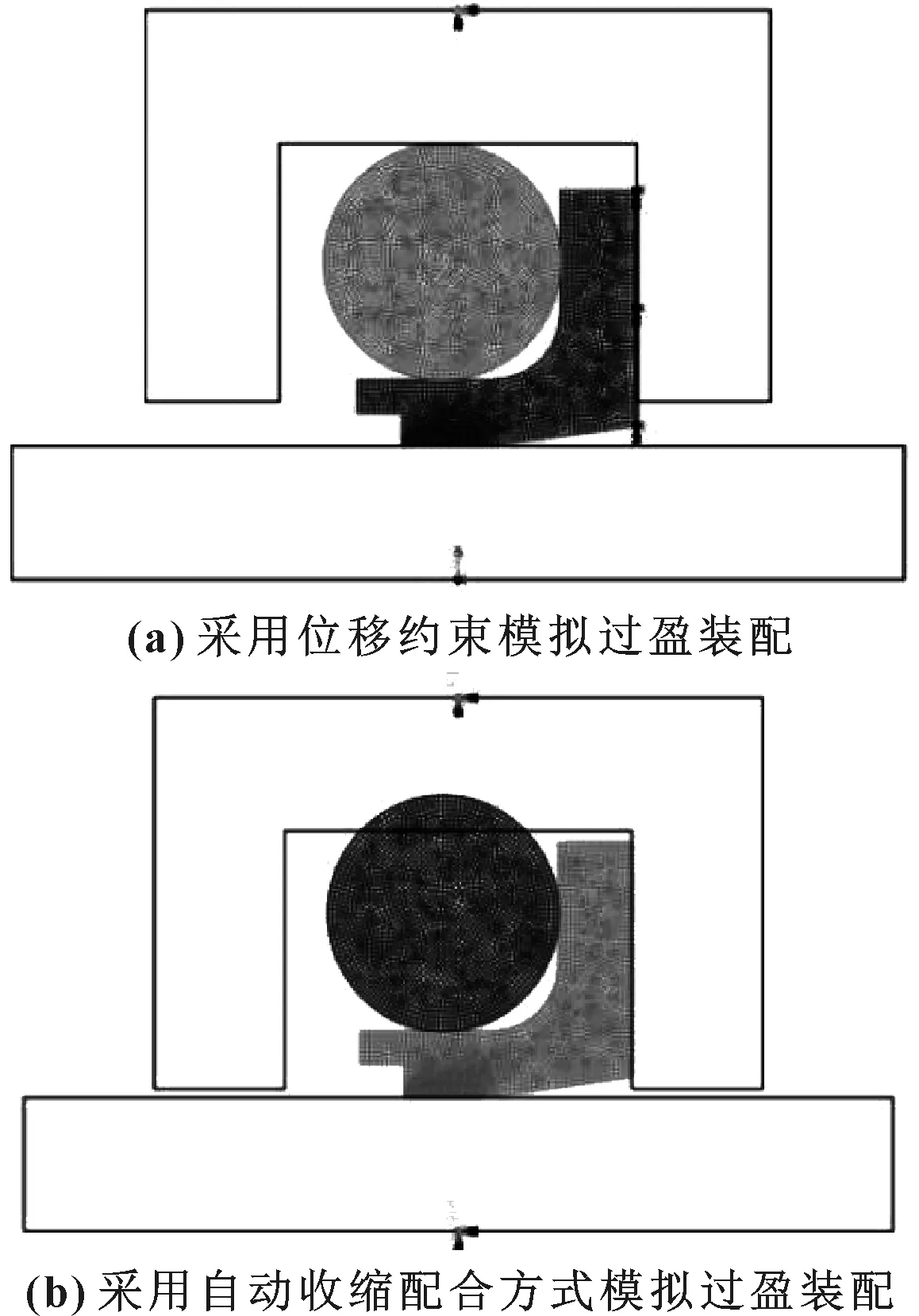
图2 过盈装配仿真模拟的有限元模型Fig 2 FEA models of interference assembly simulation (a) displacement loading method;(b)automatic shrink fit method

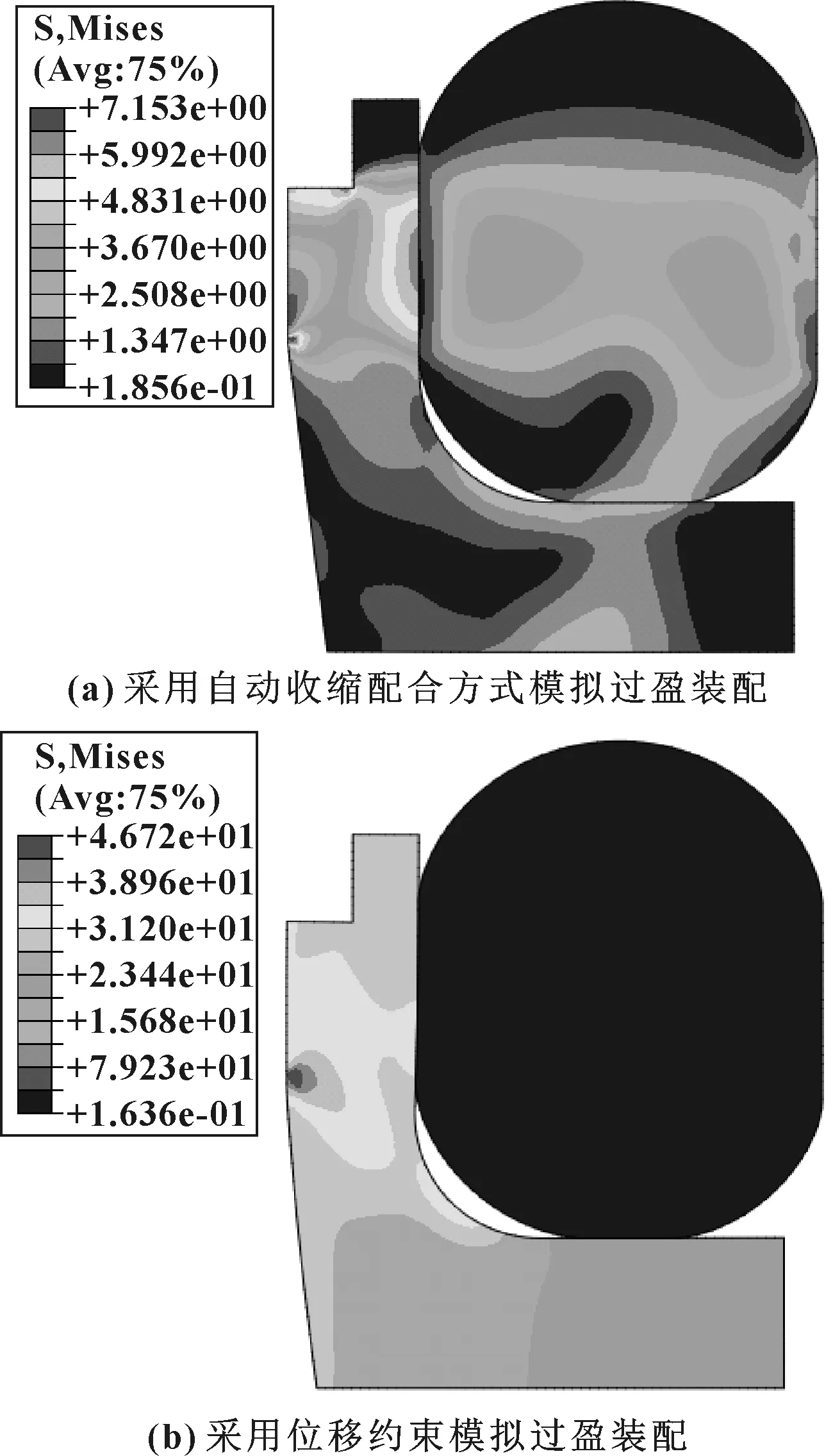
图3 采用加载方式模拟过盈装配得到的Mises应力 云图(MPa)Fig 3 The cloud maps of Mises stress with different loading methods (MPa)(a)automatic shrink fit method; (b)displacement loading method

为了进一步阐明2种加载方式对计算结果的影响，对2种加载方式产生的变形进行分析，变形情况如图4所示。从图4(a)可以看出，采用位移约束装配方式时，齿形滑环沿径向产生较大的变形，进而产生较大的Mises应力。而采用自动收缩装配方式时，最大变形出现在O形圈上，如图4(b)所示。

图4 采用加载方式模拟过盈装配得到的位移云图(MPa)Fig 4 The cloud maps of displacement with different loading methods (MPa)(a)displacement loading method; (b)automatic shrink fit method

1.4 流体侧压力加载仿真

根据ABAQUS的理论手册[15]可知,ABAQUS/Standard允许模拟流体穿透2个接触面之间的表面以及流体压力对表面的作用。它通过定义主面和从面，指定一个完全暴露在流体中的起始点,流体压力将沿着起始点向接触面加载，直到到达某个节点的流体压力小于接触压力时，停止加载。如图5所示[15]，主面由4号与5号单元组成，节点编号为201、202、203。从面由1号2号单元组成，节点编号为101、102、103。指定201为主面的起始点，101为从面的起始点。当流体通过主从接触面102号节点时，如果102号节点的流体压力小于接触压力，流体到达该节点时将会停止加载，反之将会继续向前加载。这种方法可以动态地寻找流体加载的临界点，计算得到的结果更加客观。

图5 流体压力渗透载荷施加Fig 5 Pressure penetration with nonmatching meshes

旋转动密封在稳定工作过程中，高压流体对密封圈有力的作用，并且流体会试图穿过密封的接触面。当接触面的接触压力小于流体压力时，接触节点将会被打开，流体将继续往前渗透，一直到接触面的接触压力大于流体压力时，停止流动。按照前文所述的流体压力渗透的方法来模拟，如图6(a)所示，通过定义压力渗透接触对，指定渗透起始点，指定流体压力大小，可以完成流体试图穿过密封接触界面的过程。此外，为了进行对比研究，图6(b)给出了指定边界方法模拟流体压力加载方式。

图6 不同加载方法仿真模型Fig 6 FEA models of simulation with different loading methods (a)fluid pressure penetration method; (b)boundary loading method

不同流体压力加载方式对计算结果有很大的影响，如图7所示为采用2种不同的加载方式在10 MPa的介质压力下得到的主密封面接触压力分布。其中指定边界方法需要研究者估计接触面接触与分离的临界点然后直接给定，而流体压力渗透法可以自动寻找临界点。可以看出，采用流体压力渗透法来模拟工作介质压力对密封圈的作用得到的结果更客观，主密封面接触压力分布曲线光滑，而指定边界法计算得到的接触压力分布曲线会出现不连续的点，曲线不够光滑。此外，比较图8所示的2种方式加载得到的Mises应力云图，可以明显看出指定边界法由于不能准确估计分离点会使O形圈发生畸变。

图7 不同加载方式得到的接触压力分布Fig 7 Contact pressure distribution by different loading methods

图8 不同加载方式得到的Mises应力云图(MPa)Fig 8 The cloud map of Mises stress by different loading method (MPa)(a)fluid pressure penetration method; (b)boundary loading method

2 密封圈参数敏感性分析

2.1 不同压缩率和介质压力的Mises应力分析

图9、10所示为O形圈和齿形滑环的最大Mises应力σO、σL随介质压力和O形圈压缩率的变化关系。随着介质压力的增大，σO和σL均呈现出增加的趋势，且σL的增加相对更加迅速。但是当O形圈的压缩率w=7.5%时，在介质压力超过15 MPa以后，O形圈的最大Mises应力增加速度大于齿形滑环，这是由于密封圈的压缩率太低，在高压情况下O形圈受到的变形比较大从而应力增加的速度也较大。

2.2 不同压缩率和介质压力下的接触应力分析

旋转轴与齿形滑环之间的最大接触应力pc1随介质压力和O形圈压缩率的变化如图11所示，可以看出O形圈压缩率对最大接触应力的影响要远大于介质压力。同时，由图12—14可以看出，当工作介质压力小于15 MPa时，齿形滑环与O形圈之间的最大接触应力pc2、O形圈与沟槽之间的最大接触应力pc3、齿形滑环与沟槽之间的最大接触应力pc4随工作介质压力的增加而增加，而O形圈的压缩率对其影响不大；当工作介质压力大于15 MPa时，pc2和pc3随工作介质压力的增加而增加，随压缩率的增大而减小，当O形圈的压缩率小于10%时，对其影响较大。这是由于压缩率太小会导致高压流体作用下的O形圈发生较大的形变，在局部产生应力集中，进而密封失效。此外，当密封圈在正常工作时并且工作介质压力和O形圈的压缩率相同时，pc1>pc4>pc3>pc2,说明该组合密封圈的最大接触应力满足密封的要求。

图12 齿形滑环与O形圈间最大接触应力随介质压力和 压缩率的变化Fig 12 Variation of maximum contact pressure between tooth shape combine slip ring and O-ring with medium pressure and compression ratio

图13 O形圈与沟槽间最大接触应力随介质压力和 压缩率的变化Fig 13 Variation of maximum contact pressure between O-ring and groove with medium pressure and compression ratio

图14 齿形滑环与沟槽间最大接触应力随介质压力和 压缩率的变化Fig 14 Variation of maximum contact pressure between tooth shape combine slip ring and groove with medium pressure and compression ratio

3 结论

(1)采用ABAQUS中的自动收缩配合方式来模拟密封圈的装配过程，得到的仿真结果与实际相符，同位移加载模式相比较，有效解决了主密封唇应力集中和Mises应力过大的问题。

(2)采用ABAQUS中的流体压力渗透载荷加载的方法，可以模拟高压流体穿过密封接触界面时密封圈做出的响应，从而更加有效地寻找到接触与非接触的边界节点，最终获得更真实的唇口接触宽度以及唇口接触压力分布，为密封的理论计算提供更有效的依据。

(3)有限元分析结果表明：当压缩率超过一定值10%时，在所有介质压力下，密封圈的最大Mises应力和主密封区域最大接触应力随工作介质压力的增加而增加。当压缩率低于10%，在高介质压力下产生较大的形变造成很大的应力集中。